2. Элементы теории корреляции

2.1. Линейная корреляция

Рассмотрим выборку двумерной случайной величины (Х, Y) . Примем в качестве оценок условных математических ожиданий компонент их условные средние значения, а именно: условным средним назовем среднее арифметическое наблюдавшихся значений Y, соответствующих Х = х. Аналогично условное среднее - среднее арифметическое наблюдавшихся значений Х, соответствующих Y = y. Введем уравнения регрессии Y на Х и Х на Y:

M (Y / x) = f (x), M ( X / y ) = φ (y).

Условные средние и являются оценками условных математических ожиданий и, следовательно, тоже функциями от х и у, то есть

= f*(x) - (1)

- выборочное уравнение регрессии Y на Х,

= φ*(у) - (2)

- выборочное уравнение регрессии Х на Y.

Соответственно функции f*(x) и φ*(у) называются выборочной регрессией Y на Х и Х на Y , а их графики – выборочными линиями регрессии. Выясним, как определять параметры выборочных уравнений регрессии, если этих уравнений известен.

При совместном исследовании двух случайных величин по имеющейся выборке (х₁, у₂), (х₂, у₂),…,(x_k, y_k) возникает задача определения зависимости между ними. Если вид функции y = f (x, a, b,...) задан, то требуется найти значения коэффициентов a, b,..., при которых y_i наименее отличаются от f (x_i). В методе наименьших квадратов коэффициенты должны быть такими, что принимает минимальное значение.

а) Линейная зависимость y = ax + b. Если , то из условия получаем:

б) Квадратичная зависимость y = (ax + b)². Отсюда и система для определения a, b может быть получена по аналогии с предыдущим случаем с помощью замены y_i на :

в) Показательная зависимостьЛогарифмируя, получаем: lny=ax + b, и система уравнений для a, b имеет вид:

г) Зависимость вида Тогда y² = ax + b, и условия для а и b можно задать так:

д) Логарифмическая зависимость y = ln(ax + b), то есть e^y = ax + b, и

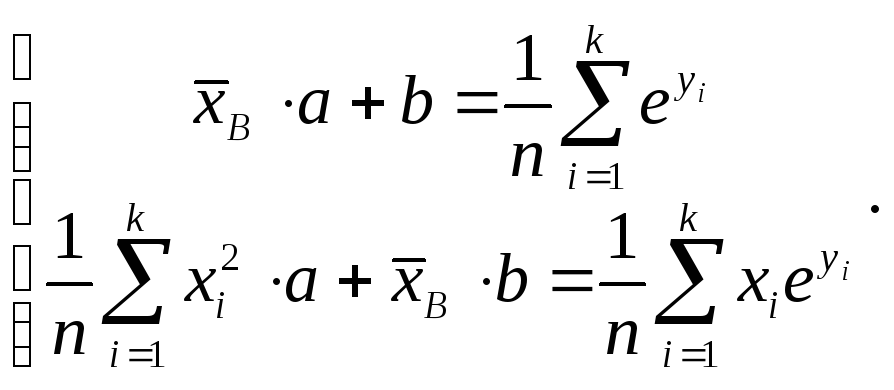
Пример. Найти параметры зависимости между х и у для выборки

xi	1,4	1,7	2,6	3,1	4,5	5,3
yi	2,5	4,7	18,3	29,8	74,2	110,4

для случаев: 1) линейной зависимости y = ax + b;

2) квадратичной зависимости y = (ax + b)²;

3) показательной зависимости y = e^{ax + b}.

Определить, какая из функций является лучшим приближением зависимости между х и у.

По виду выборки достаточно очевидно, что связь между х и у скорее всего не является линейной – у растет не пропорционально х. Проверим это предположение, найдя коэффициенты а и b для каждой из функций. Для этого вычислим предварительно = 3,1; = 40,0;

Теперь можно решать линейные системы для а и b:

1) то есть линейная зависи-мость имеет вид: у = 27,34х – 44,74.

2) квадратичная функция:

у = (2,29х – 1,68)².

3) показательная функция:

у = е^{0,94х + 0,04}.

Вычислим значения

:

yi	2,5	4,7	18,3	29,8	74,2	110,4
(yi)лин	-6,46	1,74	26,34	40,0	78,29	100,13	379,93
(yi)кв	2,33	4,9	18,27	29,37	74,4	109,35	1,397
(yi)показ	3,85	5,09	11,67	18,8	69,5	146,66	1503,81

Итак, наилучшим приближением является квадратичная функция.◄

Пусть изучается двумерная случайная величина (Х, Y), и получена выборка из п пар чисел (х₁, у₁), (х₂, у₂),…, (х_п, у_п). Будем искать параметры прямой линии среднеквадратической регрессии Y на Х вида

Y = ρ_yxx + b , (3)

Подбирая параметры ρ_ух и b так, чтобы точки на плоскости с координатами (х₁, у₁), (х₂, у₂), …, (х_п, у_п) лежали как можно ближе к прямой (3). Используем для этого метод наименьших квадратов и найдем минимум функции

. (4)

Приравняем нулю соответствующие частные производные:

.

В результате получим систему двух линейных уравнений относительно ρ и b:

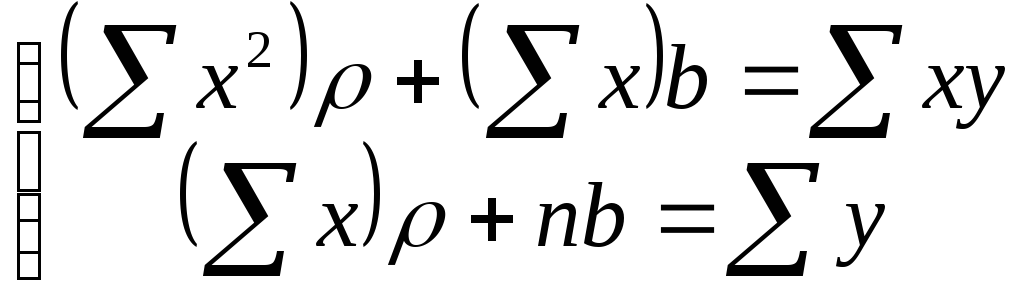. (5)

Ее решение позволяет найти искомые параметры в виде:

. (6)

При этом предполагалось, что все значения Х и Y наблюдались по одному разу.

Теперь рассмотрим случай, когда имеется достаточно большая выборка (не менее 50 значений), и данные сгруппированы в виде корреляционной таблицы:

Y	X
	x1	x2	…	xk	ny
y1 y2 … ym	n11 n12 … n1m	n21 n22 … n2m	… … … …	nk1 nk2 … nkm	n11+n21+…+nk1 n12+n22+…+nk2 …………….. n1m+n2m+…+nkm
nx	n11+n12+…+n1m	n21+n22+…+n2m	…	nk1+nk2+…+nkm	n=∑nx = ∑ny

Здесь n_ij – число появлений в выборке пары чисел (x_i, y_j). Поскольку , заменим в системе (5)

, где п_ху – число появлений пары чисел (х, у). Тогда система (5) примет вид:

. (7)

Можно решить эту систему и найти параметры ρ_ух и b, определяющие выборочное уравнение прямой линии регрессии:

.

Но чаще уравнение регрессии записывают в ином виде, вводя выборочный коэффициент корреляции. Выразим b из второго уравнения системы (7):

.

Подставим это выражение в уравнение регрессии: . Из (7)

, (8)

где Введем понятие выборочного коэффициента корреляции

и умножим равенство (8) на : , откуда . Используя это соотношение, получим выборочное уравнение прямой линии регрессии Y на Х вида

. (9)

Коэффициент корреляции – безразмерная величина, которая служит для оценки степени линейной зависимости между Х и Y: эта связь тем сильнее, чем ближе |r| к единице. Для любых переменных Х и Y абсолютная величина коэффициента корреляции не превосходит единицы: . По абсолютной величине этого коэффициента судят о силе связи между величинами: если – связь слабая, – связь умеренная, – связь сильная, – величины некоррелированные (независимые).

Для качественной оценки тесноты корреляционной связи между X и Y можно воспользоваться и таблицей Чеддока:

Диапазон изменения | rB |	0,1-0,3	0,3-0,5	0,5-0,7	0,7-0,9	0,9-0,99
Характер тесноты связи	слабая	умеренная	заметная	высокая	весьма высокая

Итак, если для выборки двумерной случайной величины (X, Y): {(x_i, y_i), i = 1, 2,..., n} вычислены выборочные средние и и выборочные средние квадратические отклонения σ_х и σ_у, то по этим данным можно вычислить выборочный коэффициент корреляции (другие обозначения )

и получить линейные уравнения, описывающие связь между Х и Y, которые называются выборочным уравнением прямой линии регрессии Y на Х:

и выборочным уравнением прямой линии регрессии Х на Y :

.

Степень приближения регрессионной линии к наблюдениям измеряется коэффициентом детерминации

,

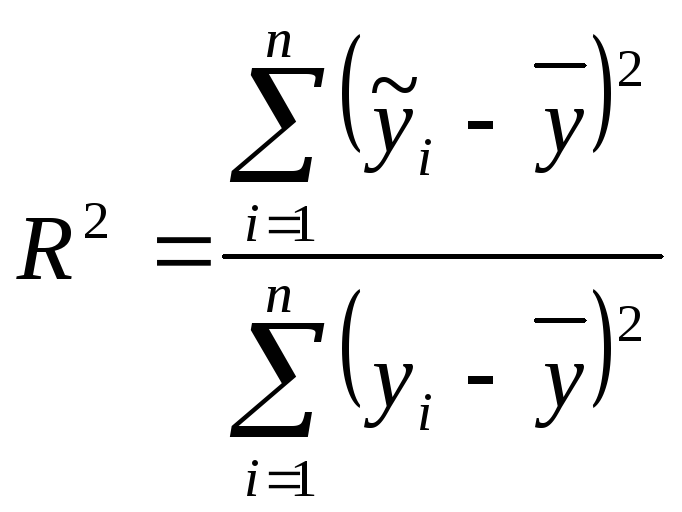где – значения, найденные по уравнению регрессии.

Коэффициент детерминации показывает, на сколько процентов найденная функция регрессии описывает связь между исходными признаками. При можно делать прогноз .

Пример. Для выборки двумерной случайной величины

i	1	2	3	4	5	6	7	8	9	10
xi	1,2	1,5	1,8	2,1	2, 3	3,0	3,6	4,2	5,7	6,3
yi	5,6	6,8	7,8	9,4	10,3	11,4	12,9	14,8	15,2	18,5

вычислить выборочные средние, выборочные средние квадратические отклонения, выборочный коэффициент корреляции и составить выборочное уравнение прямой линии регрессии Y на Х.

Для определения выборочного коэффициента корреляции вычислим предварительно Тогда

Выборочное уравнение прямой линии регрессии Y на Х имеет вид: или ◄

Пример. По данным корреляционной таблицы найти выборочный корреляционный момент (ковариацию):

X Y	-1	0	1	2
2	20	10	0	30
3	0	10	20	10

Выборочный корреляционный момент определяется равенством :

.

Здесь , - варианты (наблюдавшиеся значения) признаков и , - частота пары вариант , - объем выборки, , - выборочные средние.

Найдем выборочные средние с помощью соотношения :

, ,

где , - частоты вариант и .

Так как , получаем

,.

Тогда

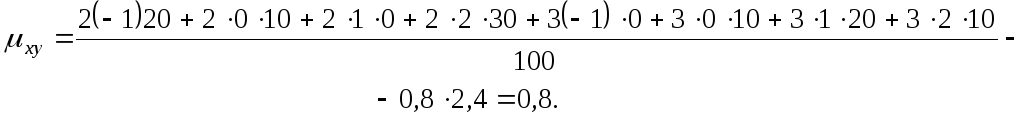
Пример. По заданной корреляционной таблице найти выборочные средние среднеквадратические отклонения _Χ, _Υ, коэффициент корреляции ρ_ΧΥ и уравнение линейной регрессии Y на X. Вычислить условные средние по дан-ным таблицы и найти наибольшее их отклонение от значений, вычисляемых из уравнения регрессии.

Y X	0	2	4	6	8	nX
1	3					3
3	2	3	5			10
5		9	8			17
7			2	6		8
9				4	1	5
11					7	7
nY	5	12	15	10	8	50

Вычислим выборочные средние и среднеквадратические отклонения для X,Y

Выборочный коэффициент корреляции между Х и У отыскивается по формуле

Согласно таблице

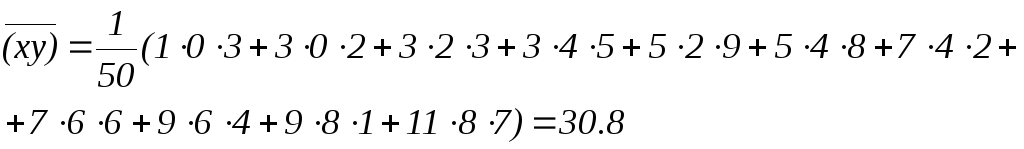
откуда

Выборочное линейное уравнение регрессии У на Х имеет вид

или, с учётом вычисленных значений,

Условное среднее при x = x_i вычисляется по формуле

где - число выборочных значений y_j , наблюдавшихся при данном x_i . Согласно данным из таблицы находим

Значения условных средних , отыскиваемые по уравнению регрессии:

Отклонения значений ,

будут d₁ = 0-0.45=-0.45; d₂ = 2.6- 1.96 = 0.65; d₃ = -0.51, d₄ = 0.55; d₅ = -0.05;

d₆ = 0.05. Наибольшее по абсолютной величине отклонение равно 0.65. ◄

Пример. Выборочно обследовано 100 снабженческо-сбытовых предприятий некоторого региона по количеству работников X и объёмам складской реализации Y (д.е.). Результаты представлены в корреляционной таблице;

X У	5	15	25	35	45	ny
130	7	1				8
132	2	7	1			10
134	1	5	4	1		11
136		1	15	10	8	34
138			3	12	15	30
140				1	6	7
nх	10	14	23	24	29	n=100

По данным исследования требуется:

1) в прямоугольной системе координат построить эмпирические ломаные регрессии Y на X и X на Y, сделать предположение в виде корреляционной связи;

2) оценить тесноту линейной корреляционной связи;

3) проверить гипотезу о значимости выборочного коэффициента корреляции, при уровне значимости α=0,05;

4) составить линейные уравнения регрессии У на X и X на У, построить их графики в одной системе координат;

5) используя полученные уравнения регрессии, оценить ожидаемое среднее значение признака Y при х=40 чел.; дать экономическую интерпретацию полученных результатов.

1. Для построения эмпирических ломаных регрессии вычислим условные средние и Вычисляем . Так как при х=5 признак Y имеет распределение

YY	130	132	134
ni	7	2	1

то условное среднее .

При х=15 признак Y имеет распределение

Y	130	132	134	136
ni	1	7	5	1

тогда .

Аналогично вычисляются все и . Получим таблицы, выражающие корреляционную зависимость Y от X (табл.2) и X от Y (табл.3).

Таблица 2

x	5	15	25	35	45
	130,8	132,86	135,74	137,08	137,86

Таблица 3

y	130	132	134	136	138	140
	6,25	14	19,54	32,35	39	43,57

В прямоугольной системе координат построим точки А_i(х_i,), соединив их отрезками, получим эмпирическую линию регрессии Y на X. Аналогично строятся точки В _j(,y_j) и эмпирическая линия регрессии X на Y (см. рис.).

Построенные эмпирические ломаные регрессии Y на X и X на Y свидетельствуют о том, что между количеством работающих (X) и объёмом складских реализаций (Y) существует линейная зависимость. Из графика видно, что с увеличением X величина также увеличивается, поэтому можно выдвинуть гипотезу о прямой линейной корреляционной зависимости между количеством работающих и объёмом складских реализаций.

2. Оценим тесноту связи. Вычислим выборочный коэффициент корреляции, предварительно вычислив характеристики по формулам

, , , , ,

, : ;

; ; ;

.

Это значение r_B говорит о том, что линейная связь между количеством работников и объемом складских реализаций высокая. Этот вывод подтверждает первоначальное предположение, сделанное исходя из графика.

3. Запишем теоретические уравнения линейной регрессии:

, .

Подставляя в эти уравнения найденные величины, получаем искомые уравнения регрессии:

1) уравнение регрессии Y на X:

, или ;

2) уравнение регрессии X на Y:

, или .

Построим графики найденных уравнений регрессии. Зададим координаты двух точек, удовлетворяющих уравнению . Пусть х = 10, тогда , А₁(10; 132,41), Если х = 40, тогда , А₂(40; 137,51). Аналогично находим точки, удовлетворяющие уравнению , В₁(10,2; 131), В₂(43; 139). Графики прямых линий регрессии изображены ниже на рисунке.

Контроль: точка пересечения прямых линий регрессии имеет координаты . В нашем примере: С(29,8; 135,78).

4. Найдём среднее значение Y при х=40 чел., используя уравнение регрессии Y на X. Подставим в это уравнение х=40, получим

.

Ожидаемое в генеральной совокупности среднее значение объёма складских реализаций при заданном количестве работников (х=40) составляет 137,51 д.е.

Замечание 1. Если в корреляционной таблице даны интервальные распределения, то за значения вариант надо брать середины частичных интервалов.

Замечание 2. Если данные наблюдений над признаками X и Y заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам:

, ,

где h₁ – шаг, т.е. разность между двумя соседними вариантами x_i; С₁ – «ложный нуль» вариант x_i (в качестве «ложного нуля» удобно принять варианту, которая расположена примерно в середине ряда); h₂ – шаг вариант Y; С₂ – «ложный нуль» вариант Y.

В этом случае выборочный коэффициент корреляции

,

где , ,

, .

Зная эти величины, находят , , σ_х, σ_у по формулам

, , , .

Найденные величины подставляем в уравнения (10).

Так в данном примере С₁ =25, h₁=10, С₂=136, h₂=2; , .

Корреляционная таблица в условных вариантах имеет вид

U V	-2	-1	0	1	2	ny
-3	7	1				8
-2	2	7	1			10
-1	1	5	4	1		11
0		1	15	10	8	34
1			3	12	15	30
2				1	6	7
nx	10	14	23	24	29	n=100

По этой таблице и приведённым выше формулам находим характеристики:

;

;

;

;

; ;

;

;

;

; .

В результате получаем те же уравнения линейной регрессии:

; .◄

Пример. Найти выборочное уравнение прямой линии регрессии:

а) на , б) на , если известны: выборочные средние , , выборочные дисперсии , , выборочный коэффициент корреляции .

а) Выборочное уравнение прямой линии регрессии на имеет вид

,

где , .

Поскольку , , получаем уравнение

, или .

б) Согласно выборочному уравнению прямой линии регрессии на :

.

Поэтому получаем

, или .◄

Пример. Некоторая фирма занимается поставками различных грузов на короткие расстояния внутри города. Перед менеджером стоит задача оценить стоимость таких услуг, зависящую от затрачиваемого на поставку времени. В качестве наиболее важного фактора, влияющего на время поставки, менеджер выбрал пройденное расстояние. Были собраны данные о десяти поставках:

Расстояние, миль	Время, мин	Расстояние, миль	Время, мин
3,5	16	1,3	11
2,4	13	1,0	8
4,9	19	3,0	14
4,2	18	1,5	9
3,0	12	4,1	16

Постройте график исходных данных, определите по нему характер зависимости между расстоянием и затраченным временем, найдите уравнение регрессии, проанализируйте силу регрессионной зависимости и сделайте прогноз времени поездки на 2 мили.

Построим диаграмму рассеяния, т.е. график исходных данных:

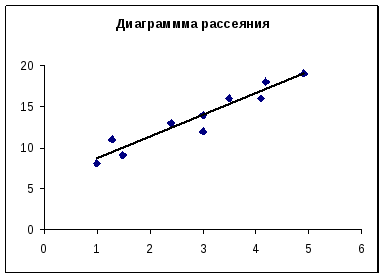
Помимо расстояния на время поставки влияют пробки на дорогах, время суток, дорожные работы, квалификация водителя, вид транспорта. Построенные точки не находятся точно на линии, что обусловлено описанными выше факторами, но эти точки собраны вокруг прямой, поэтому можно предположить линейную связь между параметрами.

Уравнение линейной регрессии , коэффициенты этого уравнения можно найти по формулам: . Расчеты поместим в таблицу.

№	x	y	х y
1	3,5	16	56	0,3721	5,76	15,222	2,632
2	2,4	13	31,2	0,2401	0,36	12,297	1,698
3	4,9	19	93,1	4,0401	29,16	18,946	28,58
4	4,2	18	75,6	1,7161	19,36	17,084	12,14
5	3	12	36	0,0121	2,56	13,893	0,086
6	1,3	11	14,3	2,5281	6,76	9,3711	17,88
7	1	8	8	3,5721	31,36	8,5732	25,27
8	3	14	42	0,0121	0,16	13,893	0,086
9	1,5	9	13,5	1,9321	21,16	9,903	13,67
10	4,1	16	65,6	1,4641	5,76	16,818	10,36
	28,9	136	435,3	15,889	122,4	136	112,4
Среднее значение	2,89	13,6	43,5	1,589	12,24	13,6	11,24

Для расчета коэффициента корреляции, коэффициентов уравнения регрессии и коэффициента детерминации имеем

;

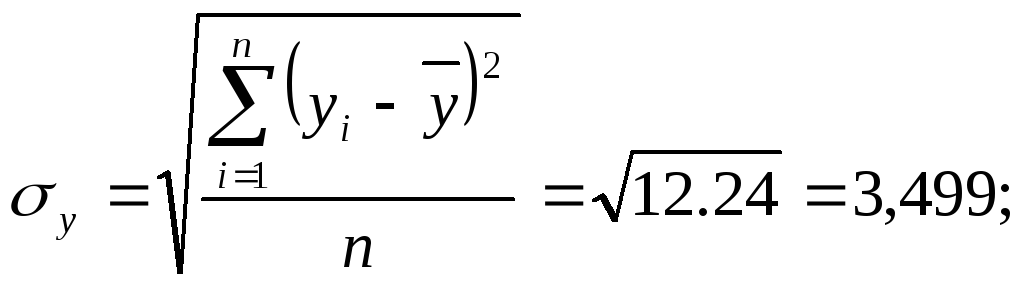
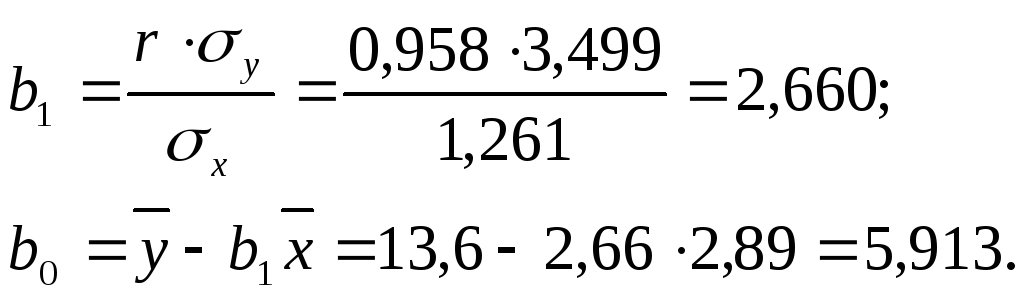
Уравнение регрессии . Наклон линии регрессии минут на милю – это количество минут, приходящееся на одну милю расстояния. Координата точки пересечения прямой с осью Oy минут – это время, которое не зависит от пройденного расстояния, а обуславливается всеми остальными возможными факторами, явно не учтенными при анализе.

Расчётные значения , найденные по этому уравнению, приведены в таблице. Правильность расчёта параметров уравнения регрессии может быть проверена сравнением сумм . В нашем случае эти суммы равны.

Коэффициент детерминации

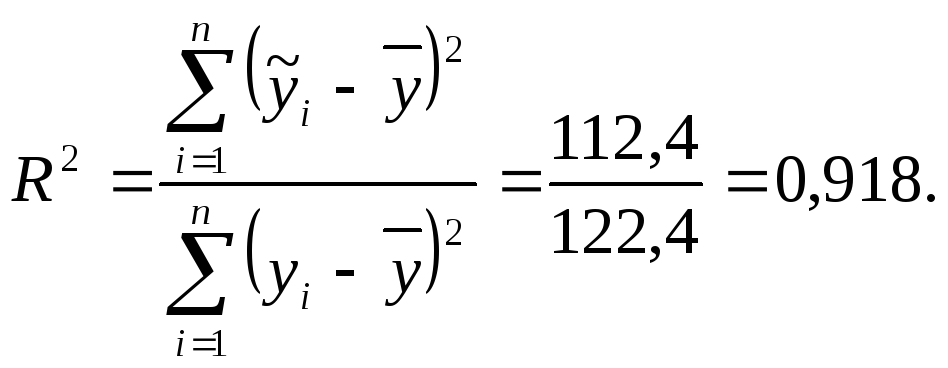
, в нашем примере , что тоже говорит о правильности расчетов.

Поскольку и расстояние 2 мили, для которого надо сделать прогноз, находится в пределах диапазона исходных данных, то можно сделать прогноз по полученному уравнению регрессии:

.

Вывод. Стоимость поставок, зависящая от времени выполнения поставок, линейно зависит от пройденного при этом расстояния.

Итак, на выполнение поставки на 2 мили потребуется 11,2 минуты. ◄