3. Доверительные интервалы для оценки среднего квадратического

отклонения нормального распределения. Будем искать для среднего квадратического отклонения нормально распределенной случайной величины доверительный интервал вида (s – δ, s +δ), где s – исправленное выборочное среднее квадратическое отклонение, а для δ выполняется условие: p ( |σ – s| < δ ) = γ.

Запишем это неравенство в виде: или, обозначив ,

. (4)

Рассмотрим случайную величину χ, определяемую по формуле

,

которая распределена по закону «хи-квадрат» с п-1 степенями свободы. Плотность ее распределения

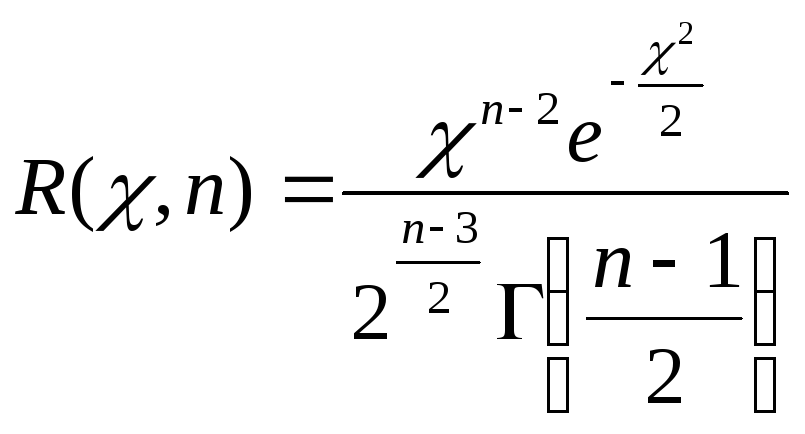
не зависит от оцениваемого параметра σ, а зависит только от объема выборки п. Преобразуем неравенство (4) так, чтобы оно приняло вид χ₁ < χ < χ₂. Вероятность выполнения этого неравенства равна доверительной вероятности γ, следовательно, Предположим, что q < 1, тогда неравенство (4) можно записать так:

,

или, после умножения на , . Следовательно, . Тогда 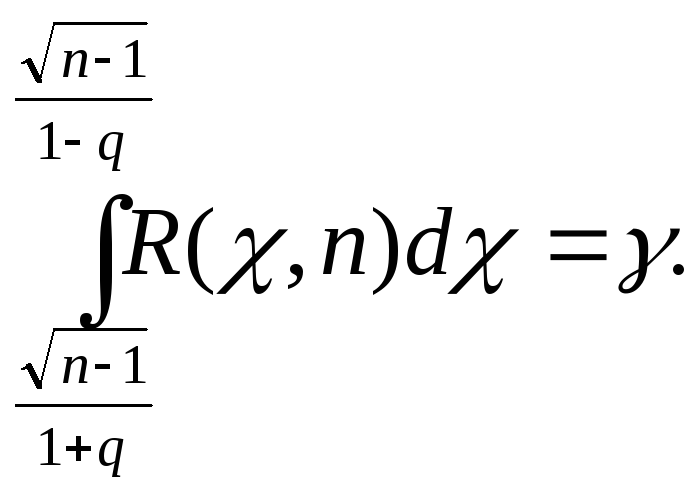Существуют таблицы для распределения «хи-квадрат», из которых можно найти q по заданным п и γ, не решая этого уравнения. Таким образом, вычислив по выборке значение s и определив по таблице значение q, можно найти доверительный интервал (4), в который значение σ попадает с заданной вероятностью γ.

Замечание. Если q > 1, то с учетом условия σ > 0 доверительный интервал для σ будет иметь границы

. (5)

Итак, для оценки генерального среднего квадратического отклонения σ при заданной надежности γ можно построить доверительный интервал вида

где s – исправленное выборочное среднее квадратическое отклонение, а

q = q (n, γ) – значение, определяемое из таблиц.

Пример. Пусть п = 20, s = 1,3. Найдем доверительный интервал для σ при заданной надежности γ = 0,95. Из соответствующей таблицы находим q (n = 20, γ = 0,95 ) = 0,37. Следовательно, границы доверительного интервала: 1,3(1-0,37) = 0,819 и 1,3(1+0,37) = 1,781. Итак, 0,819 < σ < 1,781 с вероятностью 0,95. ◄

Пример. Дана выборка значений нормально распределенной случайной величины: 2, 3, 3, 4, 2, 5, 5, 5, 6, 3, 6, 3, 4, 4, 4, 6, 5, 7, 3, 5. Найти с доверительной вероятностью γ = 0,95 границы доверительных интервалов для математического ожидания и дисперсии.

Объем выборки п = 20. Найдем = 4,25, s = 1,37. По таблицам ([1], табл. 3 и 4) определим t (0,95; 20) = 2,093; q (0,95; 20) = 0,37. Тогда

доверительный интервал для математического ожидания;

доверительный интервал для дисперсии. ◄

Пример. Служба Энергосбыта провела выборочную проверку расхода электроэнергии жителями одного из многоквартирных домов. С помощью случайного отбора было выбрано 10 квартир и определен расход электроэнергии в течение одного из летних месяцев (кВтч): 125, 78, 102, 140, 90, 45, 50, 125, 115, 112. С вероятностью 0,95 определите доверительный интервал для среднего расхода электроэнергии на одну квартиру во всем доме при условии, что отбор был: а) повторным; б) бесповторным, и во всем доме 70 квартир.

Составим таблицу

№
1	125	26,8	718,24
2	78	-20,2	408,04
3	102	3,8	14,44
4	140	41,8	1747,24
5	90	-8,2	67,24
6	45	-53,2	2830,24
7	50	-48,2	2323,24
8	125	26,8	718,24
9	115	16,8	282,24
10	112	13,8	190,44
	982		9299,6

По условию задачи: Среднее квадратичное отклонение неизвестно, поэтому заменим его несмещенной оценкой дисперсии. Имеем ;

По таблицам распределения Стьюдента найдем :

При повторном случайном отборе предельная ошибка выборки равна: т.е. доверительный интервал имеет границы

.

При бесповторном отборе предельная ошибка выборки равна: и доверительный интервал имеет границы

.

Ответ. а) При повторном отборе с вероятностью 0,95 можно ожидать, что средний расход электроэнергии в доме находится в интервале от 75,63 кВтч до 121,17 кВтч.

б) При бесповторном отборе с вероятностью 0,95 можно ожидать, что средний расход электроэнергии в доме находится в интервале от 76,93 кВтч до 119,47 кВтч.◄

Пример. С помощью случайного повторного отбора определяется средний стаж работы служащих фирмы. Предполагается, что он подчиняется нормальному закону распределения. Каким должен быть объем выборки, чтобы, с доверительной вероятностью 0,95, можно было утверждать, что, принимая полученный средний стаж работы за истинный, совершается погрешность, не превышающая 0,5 года. Стандартное отклонение равно 2,7 года?

По условию задачи и требуется найти объем выборки n при повторном отборе. Т.к. мы имеем дело с нормальным распределением, то имеем :

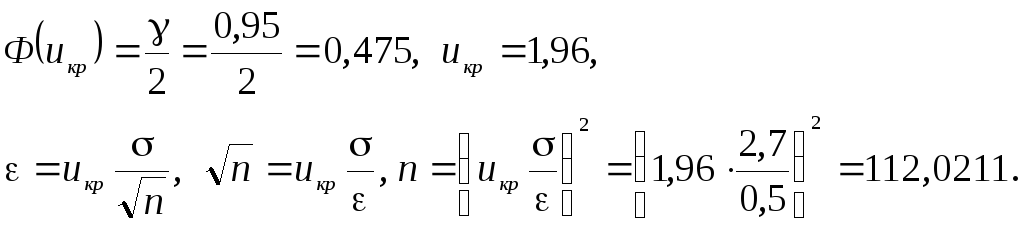
Учитывая, что необходимо не превышать заданную ошибку, округляем результат до большего целого: n = 113 служащих.

Ответ. Чтобы с вероятностью 0,95 и точностью года определить средний стаж работы в фирме, требуется опросить 113 служащих.◄