ГЛАВА ІІ
===========
ОСНОВНЫЕ МЕТОДЫ
МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
1. Выборка. Основные характеристики.
СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
Математическая статистика занимается установлением закономерностей, которым подчинены массовые случайные явления, на основе обработки статистических данных, полученных в результате наблюдений. Двумя основными задачами математической статистики являются:
1. определение способов сбора и группировки этих статистических данных;
2. разработка методов анализа полученных данных в зависимости от целей исследования.
К данным методам относятся:
а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости от других случайных величин и т.д.;
б) проверка статистических гипотез о виде неизвестного распределения или о значениях параметров известного распределения.
Для решения этих задач необходимо выбрать из большой совокупности однородных объектов ограниченное количество объектов, по результатам изучения которых можно сделать прогноз относительно исследуемого признака этих объектов. Определим основные понятия математической статистики. Генеральная совокупность – это множество {аi} всех однородных (однотипных) элементов (объектов) аi, подлежащих изучению в данном исследовании. При этом каждому элементу аi соответствует некоторое числовое значение Xi рассматриваемого признака Х.
Примером генеральной совокупности может служить работающее население региона или страны, а признаком Х, например, годовой доход работника.
Возможно сплошное обследование, когда изучается по рассматриваемому признаку каждый элемент генеральной совокупности без исключения, и выборочное обследование, когда изучению подвергается только некоторая часть элементов (подмножество) генеральной совокупности.
Выборка (выборочная совокупность) – это совокупность случайно отобранных по отдельным правилам объектов, составляющих лишь часть генеральной совокупности.
Выборка называется репрезентативной (представительной), если она правильно отражает свойства генеральной совокупности (закон и числовые характеристики признака как случайной величины). Учитывая закон больших чисел, можно утверждать, что это условие выполняется, если каждый объект выбран случайно, причем для любого объекта вероятность попасть в выборку одинакова.
Объем генеральной совокупности N и объем выборки n – число объектов в рассматриваемой совокупности. Виды выборки: повторная – каждый отобранный объект перед выбором следующего возвращается в генеральную совокупность; бесповторная – отобранный объект в генеральную совокупность не возвращается.
1. 1. Способы первичной обработки выборки
Пусть интересующая
нас случайная величина Х
принимает в выборке значение х1
п1
раз, х2
– п2
раз, …, хк
– пк
раз, причем
где п
– объем выборки. Тогда наблюдаемые
значения случайной величины х1,
х2,…,
хк
называют
вариантами,
а п1,
п2,…,
пк
– частотами.
Отношение частоты данного варианта к
общей сумме частот называется частностью
(или относительной
частотой) и
обозначается
,
,
т.е.
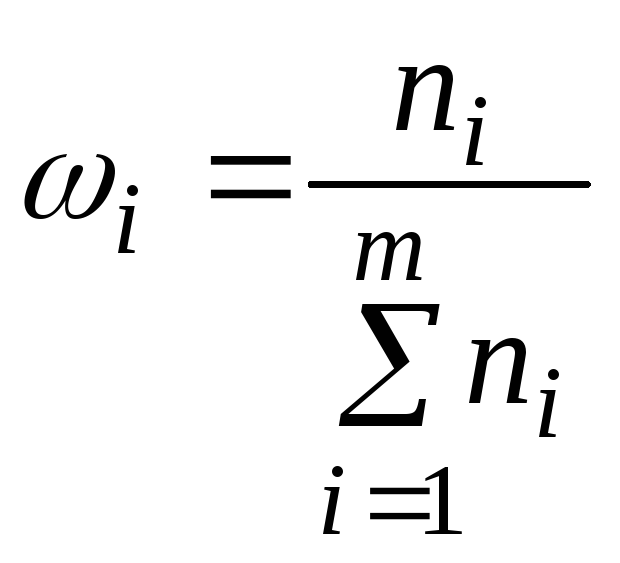или
Разность
между максимальным и минимальным
элементами выборки называется
размахом
выборки. Последовательность
вариант, записанных в порядке возрастания,
называют вариационным
рядом, а
перечень вариант и соответствующих им
частот или относительных частот –
статистическим
рядом:
|
xi |
x1 |
x2 |
… |
xk |
|
ni |
n1 |
n2 |
… |
nk |
|
wi |
w1 |
w2 |
… |
wk |
Вариационный ряд, заданный в таком виде, называют дискретным
Пример 2.1. На телефонной станции проводились наблюдения над числом Х неправильных соединений в минуту. Наблюдения в течение часа дали следующие 60 значений:
3; 1; 3; 1; 4; 1; 2; 4; 0; 3; 0; 2; 2; 0; 1; 1; 4; 3; 1; 1;
4; 2; 2; 1; 1; 2; 1; 0; 3; 4; 1; 3; 2; 7; 2; 0; 0; 1; 3; 3;
1; 2; 1; 2; 0; 2; 3; 1; 2; 5; 1; 2; 4; 2; 0; 2; 3; 1; 2; 5.
Выполним операции ранжирования (операция – ранжирование опытных данных, результатом которого являются значения, расположенные в порядке неубывания) и группировки. В результате были получены семь значений случайной величины (варианты): 0; 1; 2; 3; 4; 5; 7. При этом значение 0 в этой группе встречается 8 раз, значение 1 – 17 раз, значение 2 – 16 раз, значение 3 – 10 раз, значение 4 – 6 раз, значение 5 – 2 раза, значение 7 – 1 раз. Вычисленные значения частот и частностей приведены в табл. 2.1.
Таблица 2.1
-
Индекс
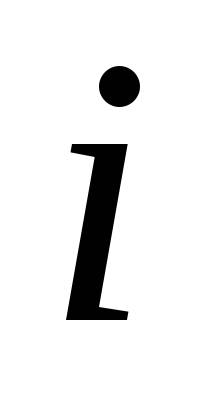
1, 2, 3, 4, 5, 6, 7
Вариант
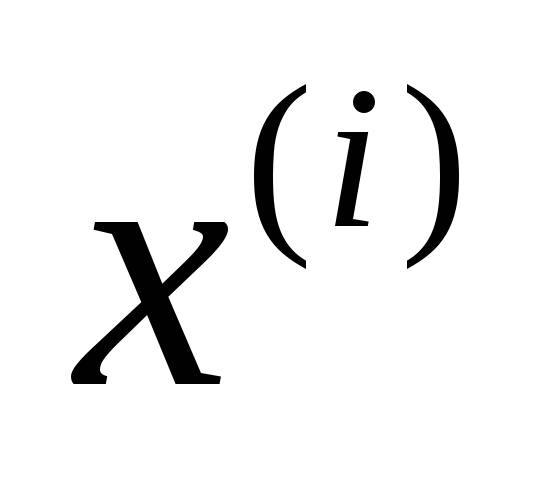
0, 1, 2, 3, 4, 5, 7
Частота
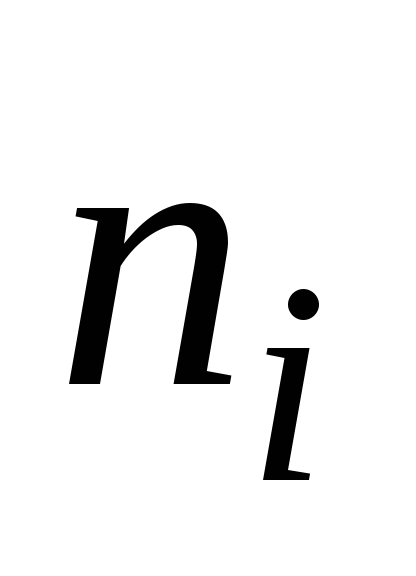
8, 17, 16, 10, 6, 2, 1
Частность
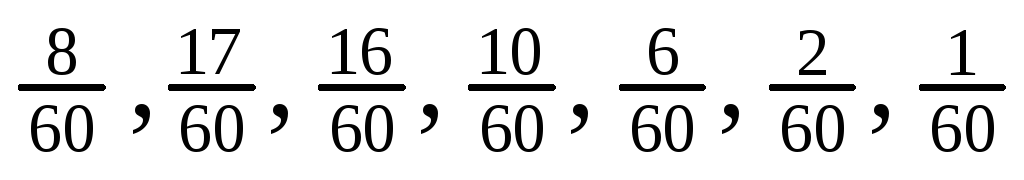
Таким образом, получен дискретный ряд:
,
где в скобках указаны соответствующие частоты. В отличие от исходных данных, этот ряд позволяет делать некоторые выводы о статистических закономерностях.
Пример. При проведении 20 серий из 10 бросков игральной кости число выпадений шести очков оказалось равным 1,1,4,0,1,2,1,2,2,0,5,3,3,1,0,2,2,3,4,1.Составим вариационный ряд: 0,1,2,3,4,5. Размах выборки равен 5. Статистический ряд для абсолютных и относительных частот имеет вид:
|
xi |
0 |
1 |
2 |
3 |
4 |
5 |
|
ni |
3 |
6 |
5 |
3 |
2 |
1 |
|
wi |
0,15 |
0,3 |
0,25 |
0,15 |
0,1 |
0,05 |
◄
Пример. Дана выборка, состоящая из чисел: 3.2, 4.1, 8.1, 8.1, 6.7, 4.4, 4.4, 3.2, 5.0, 6.7, 6.7, 7.5, 3.2, 4.4, 6.7, 6.7, 5.0, 5.0, 4.4, 8.1. Составить статистический ряд распределения абсолютных и относительных частот.
Объем выборки п = 20. Перепишем варианты в порядке возрастания:
3.2, 3.2, 3.2, 4.4, 4.4, 4.4, 4.4, 4.4, 5.0, 5.0, 5.0, 6.7, 6.7, 6.7, 6.7, 6.7, 7.5, 8.1, 8.1, 8.1. Составлен так называемый вариационный ряд, который показывает, что выборка состоит из шести вариант (3,4,5,6,7,8). Составим статистический ряд:
|
xi |
3.2 |
4.4 |
5.0 |
6.7 |
7.5 |
8.1 |
|
ni |
3 |
5 |
3 |
5 |
1 |
3 |
|
wi |
0,15 |
0,25 |
0,15 |
0,25 |
0,05 |
0,15 |
(относительная
частота
).
◄
Если число возможных значений дискретной случайной величины достаточно велико или наблюдаемая случайная величина является непрерывной, то строят интервальный вариационный ряд, под которым понимают упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами или частностями попаданий в каждый из них значений случайной величины.
Как правило, частичные интервалы, на которые разбивается весь интервал варьирования, имеют одинаковую длину и представимы в виде
,
где
число интервалов.
Длину
следует выбирать так, чтобы построенный
ряд не был громоздким, но в то же время
позволял выявлять характерные изменения
случайной величины.
Для вычисления
рекомендуется использовать следующую
формулу:
,
где
– наибольшее и наименьшее значения
случайной величины. Если окажется, что
– дробное число, то за длину интервала
следует принять либо ближайшую простую
дробь, либо ближайшую целую величину.
При этом необходимо выполнение условий:
.
После нахождения частных интервалов определяется, сколько значений случайной величины попало в каждый конкретный интервал. При этом в интервал включают значения, большие или равные нижней границе и меньшие верхней границы.
Пример 2.3.
При изменении
диаметра валика после шлифовки была
получена следующая выборка (объемом
):
-
20.3
15.4
17.2
19.2
23.3
18.1
21.9
15.3
16.8
13.2
20.4
16.5
19.7
20.5
14.3
20.1
16.8
14.7
20.8
19.5
15.3
19.3
17.8
16.2
15.7
22.8
21.9
12.5
10.1
21.1
18.3
14.7
14.5
18.1
18.4
13.9
19.8
18.5
20.2
23.8
16.7
20.4
19.5
17.2
19.6
17.8
21.3
17.5
19.4
17.8
13.5
17.8
11.8
18.6
19.1
Необходимо построить интервальный вариационный ряд, состоящий из семи интервалов.
Решение.
Так как наибольшая варианта равна 23.8,
а наименьшая 10.1, то вся выборка попадает
в интервал (10,24). Мы расширили интервал
(10.1,23.8) для удобства вычислений. Длина
каждого частичного интервала равна
.
Получаем следующие семь интервалов:
а соответствующий интервальный вариационный ряд представлен в табл. 2.2.
Таблица 2.2
|
Х |
10–12 |
12–14 |
14–16 |
16–18 |
18–20 |
20–22 |
22–24 |
|
|
|
|
|
|
|
|
|
|
☻ |
От интервального ряда можно перейти к дискретному статистическому ряду, взяв на каждом интервале (хi, xi+1) за отдельное значение хi* величину
являющуюся серединой этого интервала.