Оразец выполнения контрольной работы
ПРИМЕР 1. Решить систему линейных уравнений с помощью формул Крамера и матричным способом:
.
Решение. Находим главный определитель системы:
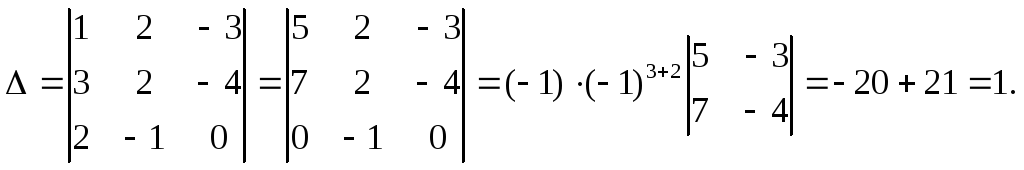
Так
как ∆≠0, то система имеет единственное
решение. Решим систему по формулам
Крамера:
где 
,
,
–
определители третьего порядка, получаемые
из определителя системы ∆ заменой
1, 2 и 3-го столбца соответственно столбцом
свободных членов -7, -4, 7.
Подставляя найденные значения в формулы Крамера, получим искомое решение:
Решим эту систему матричным способом, для чего запишем её в матричном виде:
А∙Х=В.
Здесь
Так как определитель матрицы
А отличен от нуля
,
то матрица А имеет обратную:
,
где
–
алгебраические дополнения.
Вычислим алгебраические дополнения элементов матрицы А.
Тогда
.
Матричное решение системы имеет вид:
Х=
∙В.
В нашем случае получим:
откуда следует, что
ПРИМЕР 2.
По координатам вершин пирамиды
,
,
,
найти:
-
угол между ребрами
и
, -
площадь грани
, -
уравнение плоскости
, -
уравнение высоты, опущенной из вершины
на плоскость
, -
объем пирамиды
.
Решение:
1)Угол между векторами
и
найдем по формуле
.
=(3-2)
+(2-0)
+(2-3)
=
,
.
Скалярное произведение
векторов
и
будет равно:
.
Найдем длины векторов
;
.
Тогда
Отсюда следует, что
0,33
рад, с точностью до
0,01. Это и есть искомый угол между ребрами
и
.
2) Площадь грани
равна половине площади параллелограмма,
построенного на векторах
и
,
т. е. половине модуля векторного
произведения этих векторов.
.
Следовательно,
(ед2).
3) Уравнение плоскости
напишем как уравнение плоскости через
три точки по формуле:
В нашем случае получим:
,
.
Раскрыв определитель по элементам первой строки, получим:
4)Уравнение высоты запишем
как уравнение прямой, проходящей через
т.
перпендикулярно плоскости
.
Получили каноническое уравнение прямой.
5) Объем пирамиды
найдем, используя геометрический смысл
смешанного произведения векторов.
Модуль смешанного произведения равен
объему параллелепипеда, построенного
на трех векторах. Объем пирамиды равен
объема
параллелепипеда, построенного на
векторах
,
,
.
Смешанное произведение трех векторов
в координатной форме записывается как
определитель третьего порядка,
составленный из координат этих векторов.
В нашем случае:
=(1;
2; -1),
= (0; 2; 2),
= (-1; 1; -2).
ПРИМЕР 3. Найти пределы функций, не пользуясь правилом Лопиталя:
1)
; 2)
;
3)
; 4)
.
Решение
1) Подстановка предельного
значения приводит к неопределённости
вида (
),
которая раскрывается путём деления
числителя и знаменателя на старшую
степень аргумента.
,
поскольку при
функции
,
,
,
являются бесконечно малыми.
2) Подстановка предельного
значения в этом примере приводит к
неопределённости вида (
).
Чтобы раскрыть эту неопределённость,
разложим числитель и знаменатель на
простейшие множители:
3) Чтобы найти
,
воспользуемся первым
замечательным пределом
,
предварительно освободившись от
иррациональности в числителе :
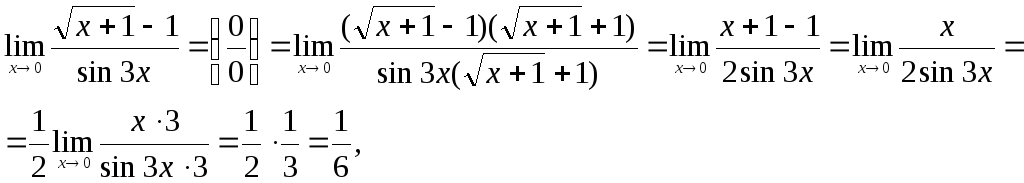
так как
.
4) Подстановка предельного
значения в четвёртом примере приводит
к неопределенности вида (
),
которая раскрывается с помощью второго
замечательного предела:
ПРИМЕР 4. Исследовать функцию на непрерывность. Сделать схематический чертёж.
1)
если
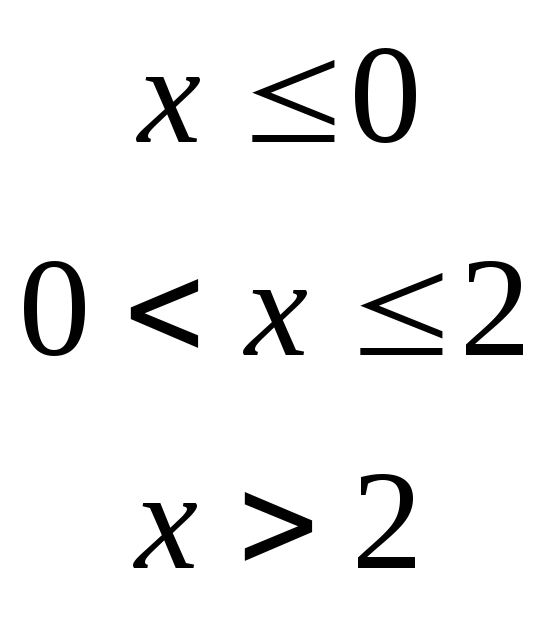2)
.
Решение
1) В первом случае задана неэлементарная функция. Точками разрыва такой функции могут быть точки, в которых меняется аналитическое задание функции. В нашем примере это точки х=0 и х=2. Исследуем на непрерывность функцию в этих точках.
Найдём односторонние пределы:
,
и найдём значение функции
при х = 0:
Здесь f(-0)
= f(+0) = f(0),
следовательно, функция в
точке х = 0 непрерывна.
,
здесь односторонние пределы не равны, но являются конечными числами. Поэтому точка х=2 является точкой разрыва I рода. Сделаем схематический чертёж
Рис.1
2) Функция
является элементарной и непрерывна на
всей области определения. Поскольку в
точке х=4 она не определена, то х=4 – точка
разрыва функции. Исследуем характер
разрыва. Найдем односторонние пределы
функции в точке х=4.
Так как один из пределов равен ∞, то х=4 – точка разрыва II рода.
Сделаем схематический чертёж.
Рис.2
ПРИМЕР 5. Найти производные заданных функций.
a)
.
Решение.
Производную данной функции найдём как
производную произведения двух функций
по формуле
.
б)
Решение. Производную данной функции найдём, используя правило дифференцирования сложной функции.
в)
Решение. Данная функция является степенно-показательной. Прологарифмировав данную функцию по основанию e, получим:
.
Дифференцируем обе части этого равенства по х, учитывая, что у является функцией от х.
,
откуда
г)
Решение. Производную неявно заданной функции найдём, дифференцируя обе части уравнения по переменной х, считая у функцией от х.
;
=
;
д) Найти производную параметрически заданной функции:
Решение. Производная функции, заданной параметрически, находится по формуле
, 
.
Тогда
.
ПРИМЕР 6. Найти экстремумы функции
Решение. Найдем стационарные точки
Решив систему, получим
.
Найдена одна стационарная точка
Проверим наличие экстремума в точке
с помощью достаточных условий:
откуда
Так как
то в точке
функция имеет минимум.
В О П Р О С Ы для подготовки к экзамену