§ 4. Системи лінійних нерівностей

Нехай у двовимірному просторі задано п лінійних нерів­ностей з двома невідомими

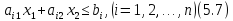
Кожна нерівність виду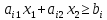 множенням її на - 1 зводиться до виду (5.7).

Як було вже показано, кожна нерівність системи (5.7) визначає одну з двох півплощин, на які пряма , поділяє площину. Гранична пряма 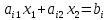< перпендикулярна до вектора , ( ).

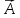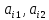Кожну пару чисел (точку площини), що задовольняє всі нерівності системи (5.7), називають розв'яжем даної системи.

Наведемо кілька прикладів.

1 Нерівність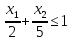, або 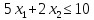визначає півплощину, яка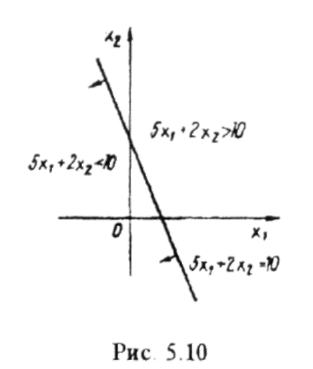

розміщена під граничною прямою перпендикулярна до

вектора (5, 2) (рис. 5.10)

2. Дві нерівності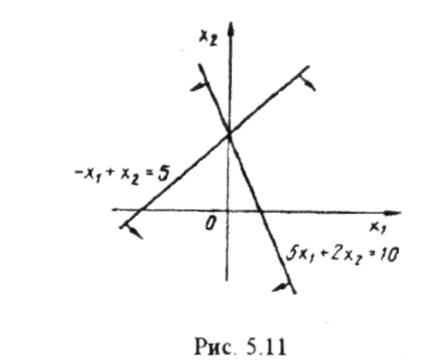

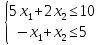
визначають частину площини, зображену на рис. (5.11). Розв'язком цієї системи нерівностей є перетин (спільна частина) півплощин, які визнача­ються кожною нерівністю системи

З Розв'язком системи трьох нерівностей

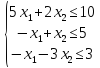
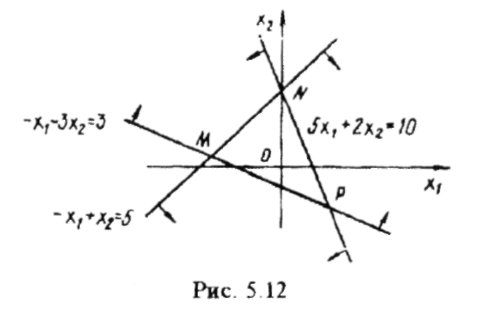
є множина точок площини, які утворюють трикутник MNP(puc. 5.12), який є перетином півплощин, що визначаються кожною з нерівностей системи.

4. Розв'язком системи чотирьох нерівностей

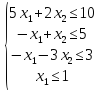
є множина точок площини, яка утворює чотирикутник MNPQ (рис 5.13).

5. Розв'язком системи семи нерівностей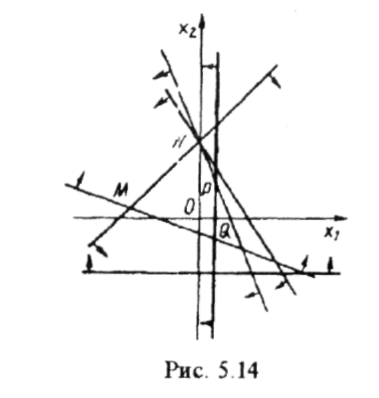

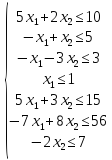
є чотирикутник MNPQ (рис. 5 14). Плошини, що визначаються нерів­ностями , повністю містять у собі чотирикутник MNPQ.

6. Розв'язком системи п'яти нерівностей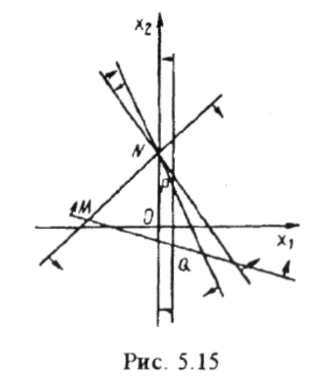

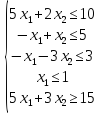
є одна точка N (0, 5) (рис 5.15). Чотирикутник MNPQ і півплощина, яка визначається нерівністю 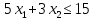, мають одну спільну точку N.

7. Система шести нерівностей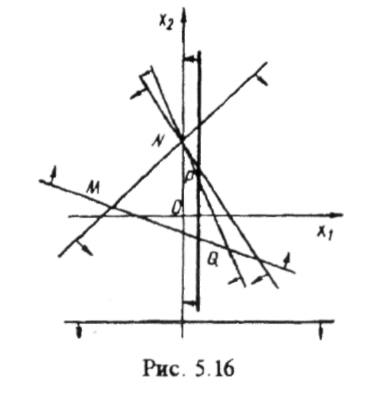

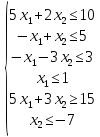
є несумісною (рис. 5 16).

Проаналізувавши наведені приклади, можна дійти таких висновків.

1. Система нерівностей може бути сумісною. У цьому разі є принаймні одна точка площини, що належить усім півплощинам, які визначаються кожною з не­рівностей системи. Множина точок, яка є розв'язком системи нерівностей, може бути пшплощиною, обме­женим або необмеженим многокутником, прямою чи її відрізком, точкою.

Сукупністю точок, що задовольняють систему не­рівностей (множину її розв'язків), є опукле тіло.

2. Система нерівностей може бути несумісною.

У тривимірному просторі систему п лінійних нерівностей можна записати у вигляді

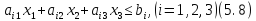
Кожна нерівність системи (5.8) визначає півпростір з граничною площиною 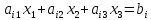перпендикулярною до вектора 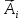( 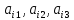).Розв'язком системи нерівностей (5.8) є сукупність точок простору, спільних для всіх півпросторів, що визначаються нерівностями системи. Якщо система сумісна, то множиною її розв'язків є опукла множина, яка може бути півпростором, многогранником (обмеженим або необмеженим), площи­ною, многокутником, прямою, відрізком прямої, точкою.

У сумісній системі серед її нерівностей можуть бути й зайві, тобто такі, після вилучення яких множина розв'язків не зміниться. Так, у прикладі 5 нерівності п'ята, шоста і сьома — зайві.

Зайві нерівності можуть бути двох видів:

1. нерівності, граничні прямі (площини) яких не пере­тинаються з множиною розв'язків системи (шоста і сьома нерівності у прикладі 5);

2. нерівності, граничні прямі (плопшни) яких є опорними для множини розв'язків (п'ята нерівність у прикладі 5).

Якщо півпростори, що визначаються нерівностями си­стеми, не мають спільних точок, то система нерівностей несумісна.

Нехай в m-вимірному просторі задано систему нерів­ностей

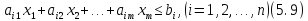
За аналогією з дво- і тривимірним просторами кажуть, що кожна з нерівностей системи (5.9) визначає в m-вимірному просторі півпростір з граничною гшерплощиною.

Якщо існує принаймні одна точка, спільна для всіх півпросторів, що визначаються нерівностями системи (5.9), то систему називають сумісною, у противному разі — несумісною.

Множиною розв'язків системи нерівностей (5.9) є опукла множина в m-вимірному просторі. Справді, досить показати, що коли X₁ і Х₂ — два розв'язки системи (5.9), то будь-яка лінійна комбінація їх 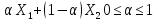, також буде розв'язком цієї системи. Запишемо систему (5.9) у векторно-матричній формі

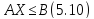
де А — матриця коефіцієнтів при невідомих, X — невідомий вектор, В — вектор вільних членів.

Підставивши 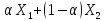у нерівність (5.9) і враху­вавши, що X₁ і Х₂ є розв'язками, дістанемо

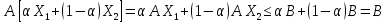
що і треба було довести.