§ 2. Поняття про відрізок в п-вимірному просторі

Розглянемо на площині дві точки М₁ і М₂ та їхні радіуси-вектори (рис. 5.3).

Вектор . Якщо вектор помножити на t (0 ≤ t≤ 1), то дістанемо вектор , колінеарний век­тору і напрямлений так само як і вектор , оскільки t ≥ 0. Якщо початок вектора помістити в точку М₁ то його кінець M буде всередині відрізка .

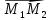При t = 0 вектор і точка М збігається з точкою М₁ при t = 1 вектор = , і точка М збігається з точкою М₂. Якщо t зростає від 0 до 1, то точка М пробігає відрізок від M₁ до М₂.

Радіус-вектор дорівнює сумі векторів i тобто

При зростанні t від 0 до 1 кінець радіуса-вектора пробігає відрізок М₁М₂.

Отже, радіус-вектор будь-якої точки М, що лежить на відрізку М₁М₂, визначається рівнянням

Наведені міркування переносяться й на тривимірний про­стір.

Узагальнивши ці міркування на випадок n-вимірного про­стору, природно вважати, що відрізком М₁М₂ n-вимірного простору є сукупність точок М, радіуси-вектори яких зада­ються рівнянням (5.2).

У скалярній формі рівняння (5.2) має вигляд

Тут () і () є координатами точок M₁ і М₂ або радіусів-векторів і .

§ 3. Опуклі множини

!Означення

Сукупність точок n-вимірного простору називають опуклою множиною або тілом, якщо юно разом з будь-якими двома своїми точками М₁ і М₂ містить і весь відрізок M₁M₂ що їх сполучає (рис. 5.4).

Фігура, зображена на рис. 5.5, не є опуклою множиною. Справді, відрізок, що сполучає точки M₁, і М₂, не належить повністю фігурі.

!Означения

Перерізом множин називають сукупність точок, що належать кожній з цих множин.

Теорема

Переріз будь-якої кількості опуклих множин є також опуклою множиною.

Доведення. Розглянемо дві будь-які точки М₁ і М₂ перерізу. Ці точки належать кожній з перетинних множин. Проте ці множини опуклі, тому відрізок належить кожній з них, а отже, належить і перерізу їх, тобто переріз є опуклою множиною.

Теорему доведено.

!Означення

Опуклою лінійною комбінацією точок А₁,А₂,А_т n-вимірного лінійного простору називають точку

При т = 2 опукла лінійна комбінація збігається з точкою відрізка.

Справді, якщо позначити , то рівняння відрізка (5.2) набере вигляду , тобто довільний вектор (точка) відрізка є опуклою лінійною комбінацією векторів (точок) . Справедливим є й обер­нене твердження: будь-яка точка, що є лінійною комбінацією двох точок n-вимірного простору, лежить на відрізку, що сполучає ці точки.

Щоб довести це, досить в лінійній комбінації позначити

!Означення

Кутовими або крайніми точками опуклої множини називають точки, які не є опуклими лінійними комбіна­ціями двох будь-яких довільних точок цієї множини.

Так, якщо множиною M є відрізок, що сполучає деякі дві точки n-вимірного простору М₁ і М₂ то ці точки є кутовими точками множини М, оскільки їх не можна визначити як лінійні комбінації будь-яких інших точок відрізка.

У трикутнику ABC є три кутові точки — його вершини (рис. 5.6).

Щодо будь-якої іншої точки трикутника (як граничної, так і внутрішньої), то вона є опуклою лінійною комбіна­цією вершин А, В і С. Для точок, що лежать на сторонах АВ, ВС і СА, це твердження випливає з означення відрізка.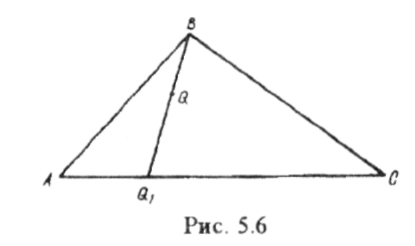

Покажемо, що будь-яка внутрішня точка Q трикутника також є опуклою лінійною комбінацією вершин А, В і С. Для цього через точки В і Q проведемо пряму до перетину зі стороною АС у деякій точці Q₁ Точку Q₁ можна подати як лішйну комбінацію точок А і С.

Точку Q, як точку відрізка BQ₁ також можна подати у вигляді лінійної комбінації точок В і Q₁ тобто Підставивши сюди значення Q₁ дістанемо вираз

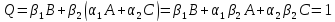
який є опуклою лінійною комбінацією. Справді,

і всі коефіцієнти невід'ємні. Отже, Q є опук­лою лінійною комбінацією точок А, В і С

!Означення

n-Вимірним симплексом називають множину векторів (точок) А () n-вимірного простору, що за­довольняє умову

Двовимірним симплексом є відрізок, що лежить у першій чверті і відтинає на осях координат одиничні відрізки (рис. 5.7, а); тривимірним симплексом є трикутник, який розміщений у додатному октанті; він відтинає на осях ко­ординат одиничні відрізки (рис. 5.7, б).

Нехай в n-вимірному просторі задано l точок P₁ Р₂,….Р_l,. Множину точок

утворену при всіх можливих змінах величин , що задовольняють умову , називають лінійною оболонкою точок P₁ Р₂,….Р_l .Справедливим є таке твердження.

Теорема

Будь-яка опукла множина М містить лінійну оболонку кожної своєї підмножини.

Доведення. При l = 2 це твердження відповідає оз­наченню опуклої множини.

Нехай l = 3. Візьмемо три довільні точки P₁ Р₂,….Р_l, що належать М, і розглянемо їхню лінійну оболонку

Зафіксуємо деякі значення і утворимо вектор = (), що належить тривимірном симплексу (рис. 5.8).

Проведемо через вектор площину, перпендикулярну до площини де, x₁Ох₂ і подамо вектор у вигляді суми двох векторів: де , Оскільки вектор належить двовимірному симплексу (), де , , 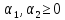то йому відповідає вектор

Виразимо значення через . З прямокутни­ків OKNL і OK'N'L маємо:

OK=; OL =; ОК' = ; OL’=,

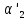або

Аналогічно , звідки

Тоді

Оскільки P₃ і P₄ належать множині M, , то вектор Q належить опуклій множині M, що й треба було довести.

Методом індукції доведення переноситься на будь-яке число l.

З доведеної теореми випливає, що кожній під множині точок Р_і опуклої множини М можна поставити у відповідність принаймні одну точку Р з М, що належить лінійній оболонці точок P_i. Обернене твердження справджується не завжди.

Кутові точки множини не належать лінійній оболонці інших точок цієї множини.

!Означення

Опуклу лінійну оболонку скінченного числа точок на­зивають опуклим многогранником.

Кутові точки многогранника називають його вершинами, відрізки, що сполучають дві сусідні вершини, називають ребрами; плоскі многокутники, що обмежують многогранник, називають його гранями.

Як було вже показано, трикутник є опуклою лінійною оболонкою трьох його кутових точок (вершин).

Ця властивість характерна для всіх опуклих многогран-ників.

Т е о р е м а

Якщо М — опуклий многогранник, а — множина його кутових точок то, M є опуклою лінійною оболонкою множини .

Доведення. Нехай М є опуклою лінійною оболон­кою точок A₁ А _2,…,А_п. Тоді будь-яка кутова точка множини Mє однією з точок А_i, оскільки кутові точки не можуть бути лінійними комбінаціями інших точок.

Виберемо серед точок А_i. мінімальну під множину, опук­лою лінійною оболонкою яких є множина М. Припустимо, що такою підмножиною є A_1,A₂, ...,А_r. Тоді кожна з цих точок є кутовою. Якщо, наприклад,

то

А = А'+А_Г.

Справді, виразивши А і А' через А _і, матимемо

Підставивши рівності (5.5) у рівність (5.4), дістанемо, що А_r, є опуклою комбінацією векторів А_i :

Нехай μ_r < 1, тоді

що суперечить мінімальності підмножини A₁ А₂,…,А_n.

Крім того, якщо μ_r = 1, то μ_i = 0 для i≠r. Визначивши μ_i через і , знаходимо, що

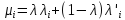
Отже, для i≠r виконується рівність

Звідси = =0. Отже,

Теорему доведено.

Таким чином, на основі цієї теореми опуклий много­гранник можна розглядати як множину, що є опуклою лі­нійною оболонкою множини його кутових точок (вершин). Наприклад, куб є опуклою лінійною оболонкою восьми його вершин.

!Означення

Опорною прямою многокугника називають пряму, яка має з ним принаймні одну спільну точку, і таку, що весь многокутник лежить з одного боку від неї (рис. 5.9).

Прямі АВ, CD, MN, PQ, TS — опорні. Опорна пряма може мати з опуклим многокутником спільну частину, яка складається з однієї точки (прямі АВ, MN) або з відрізка (пряма CD).

Аналогічно опорною площиною опуклого многогранника називають площину, яка має з многогранни­ком принаймні одну спільну точку, і таку, що весь многогранник лежить з одного боку від цієї площини.

Опорна площина може мати з многогранником спільну частину, яка складається з однієї точки (вершини много­гранника); з відрізка (ребра многогранника) або з много­кутника (грані многогранника).

Як бачимо, через кожну вершину і кожне ребро много­гранника можна провести нескінченну кількість опорних площин, а через будь-яку грань многогранника проходить тільки одна опорна площина.