2.1. Понятие вектора. Линейные операции над векторами

Схема 1

Схема 2

С линейными операциями над векторами связаны понятия коллинеарные векторы, компланарные векторы, линейно зависимые и линейно независимые векторы.

Схема 3

Схема 4

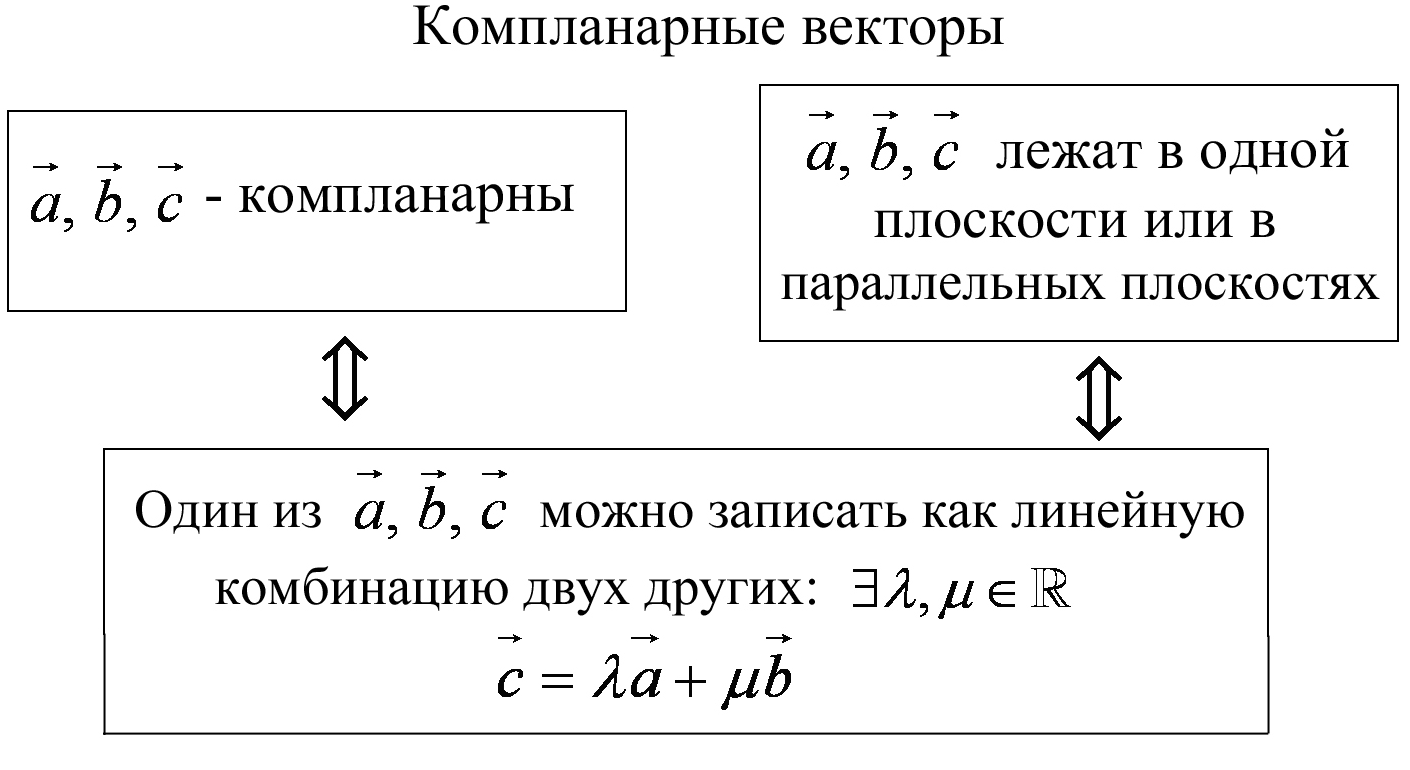
Пара коллинеарных векторов и тройка компланарных векторов служат примерами пары и тройки линейно зависимых векторов. Пара неколлинеарных векторов на плоскости и тройка некомпланарных векторов в пространстве служат примерами линейно независимых систем векторов и составляют соответственно базисы систем векторов плоскости и пространства.

2.2. Линейная зависимость векторов. Базис системы векторов

Свойства линейно зависимых и линейно независимых векторов.

1. Если система векторов содержит , то ее векторы линейно зависимы.

2. Если часть системы векторов линейно зависима, то и вся система линейно зависима.

3. Всякая часть линейно независимой системы векторов линейно независима.

4. Если векторы  – линейно независимы, а векторы - уже линейно зависимы, то вектор является линейной комбинацией векторов .

5. Если все векторы являются линейными комбинациями системы векторов и то векторы  – линейно зависимы.

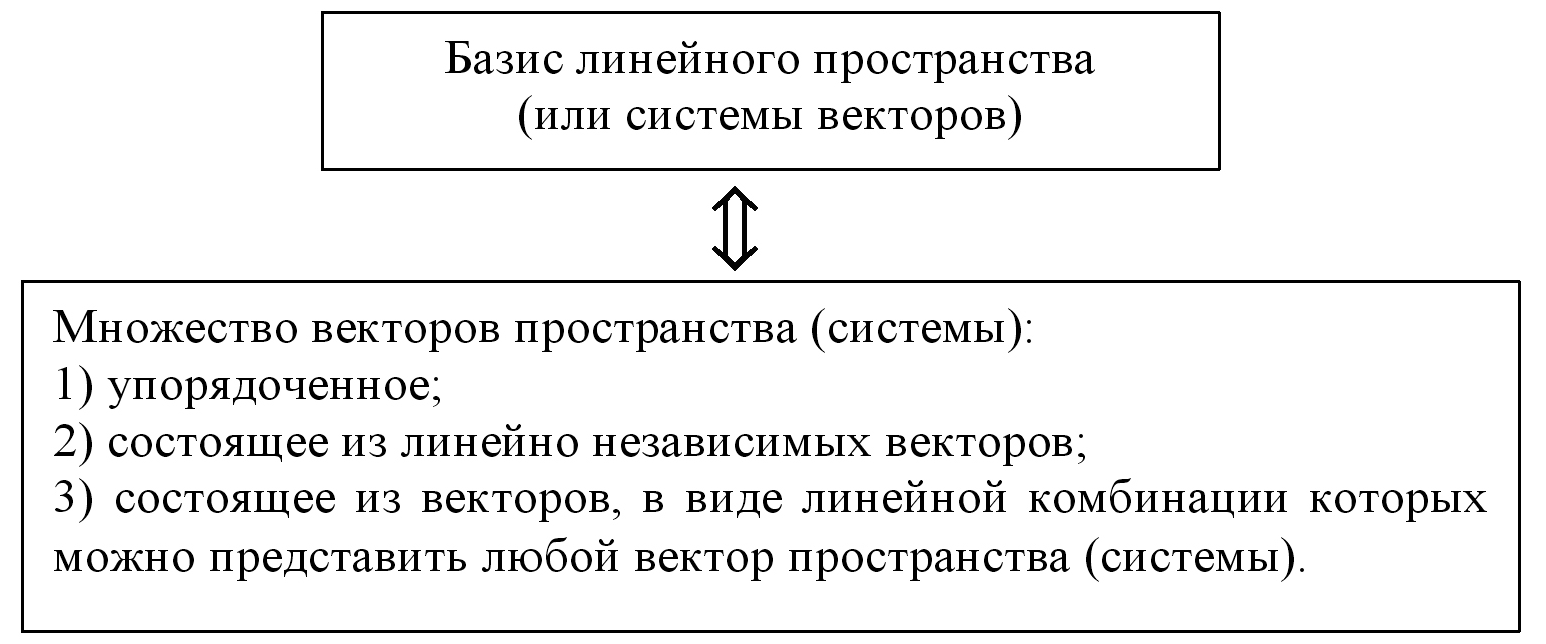
Итак, данное определение означает следующее:

Понятие базиса позволяет определить вектор в заданном пространстве упорядоченным набором чисел – его координатами.

2.3. Понятие системы координат. Координаты точки

Схема 5

Найти координаты вектора в данном базисе – это значит разложить этот вектор по базисным, т.е. представить вектор в виде линейной комбинации базисных векторов. Коэффициенты этой линейной комбинации и будут координатами вектора.

Разложение вектора по заданным векторам (заданным направлениям) часто применяется в теоретической механике, а также при изучении ряда технических вопросов. Так, например, при взлете самолета важна не только скорость самолета, но и его «скороподъемность», то есть вертикальная составляющая скорости. При движении тела, брошенного с некоторой первоначальной скоростью, рассматривают не только скорость «вдоль траектории, но и горизонтальную и вертикальную составляющие этой скорости.

Задачи следующего параграфа призваны привить навыки геометрического выполнения линейных операций над векторами и помочь усвоить понятие координат вектора относительно заданного базиса.

2.4. Задачи и упражнения

1. Пусть параллелограмм, – точка пересечения его диагоналей, а точки –соответственно середины сторон и Выполнить следующие операции: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13)

2. Написать векторные равенства, связывающие векторы, изображенные на рисунках:

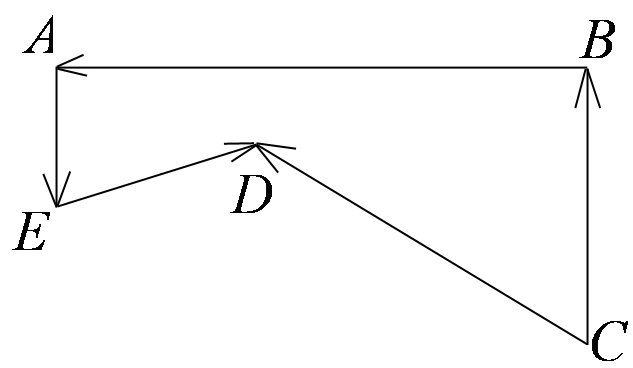
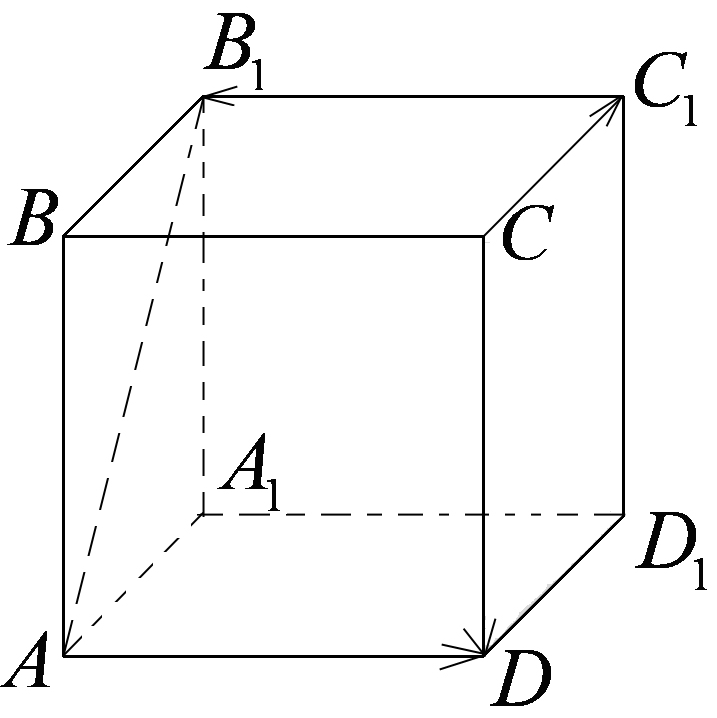
3. Дан прямоугольный параллелепипед Точки  – середины ребер соответственно. Указать векторы, равные следующим векторам: 2) 3) 4)

4. Пусть и – медианы треугольника Выразить векторы через векторы

5. Пусть – произвольный треугольник, а и середины сторон и Выразить векторы и через векторы

6. В тетраэдре точка лежит на ребре и делит отрезок в отношении Полагая выразить через векторы векторы

7. Даны треугольник и произвольная точка Пусть  – середины сторон соответственно. Доказать, что равнодействующая сил равна равнодействующей сил

8. Пусть параллелограмм, – точка пересечения его диагоналей, а и середины противоположных сторон и Взяв за базисные векторы и определить в этом базисе координаты следующих векторов:

9. Решить предыдущую задачу в предположении, что за координатные векторы приняты векторы и

10. В треугольнике проведены медиана и средняя линия параллельная стороне Прямые и пересекаются в точке Найти: а) координаты векторов принимая за базисные векторы и в) координаты тех же векторов, принимая за базисные векторы и векторы и

11. В основании пирамиды лежит параллелограмм – точка пересечения его диагоналей, и – середины ребер и соответственно. Разложите векторы по векторам

12. – центр правильного шестиугольника Полагая выразите векторы через и Запишите координаты перечисленных векторов в базисе

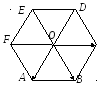
Рис. 1

13. В тетраэдре точка делит сторону в отношении а точка является центроидом грани (точкой пересечения медиан треугольника ). Разложите векторы по векторам Запишите координаты указанных векторов в базисе

14. Диагонали основания пирамиды пересекаются в точке Найдите координаты векторов и в базисе, состоящем из векторов

2.5. Специальные произведения векторов

Специальными произведениями векторов называют скалярное и векторное произведение двух векторов, а также смешанное и двойное векторное произведение трех векторов.

Эти произведения находят широкое применение не только в геометрии, но и в различных разделах физики. Следующие схема знакомят нас с определениями указанных произведений, их свойствами и основными приложениями.

2.5.1. Скалярное произведение двух векторов

Схема 6

Приложения скалярного произведения

Схема 7

2.5.2. Векторное произведение двух векторов

Схема 8

Приложение векторного произведения

Схема 9

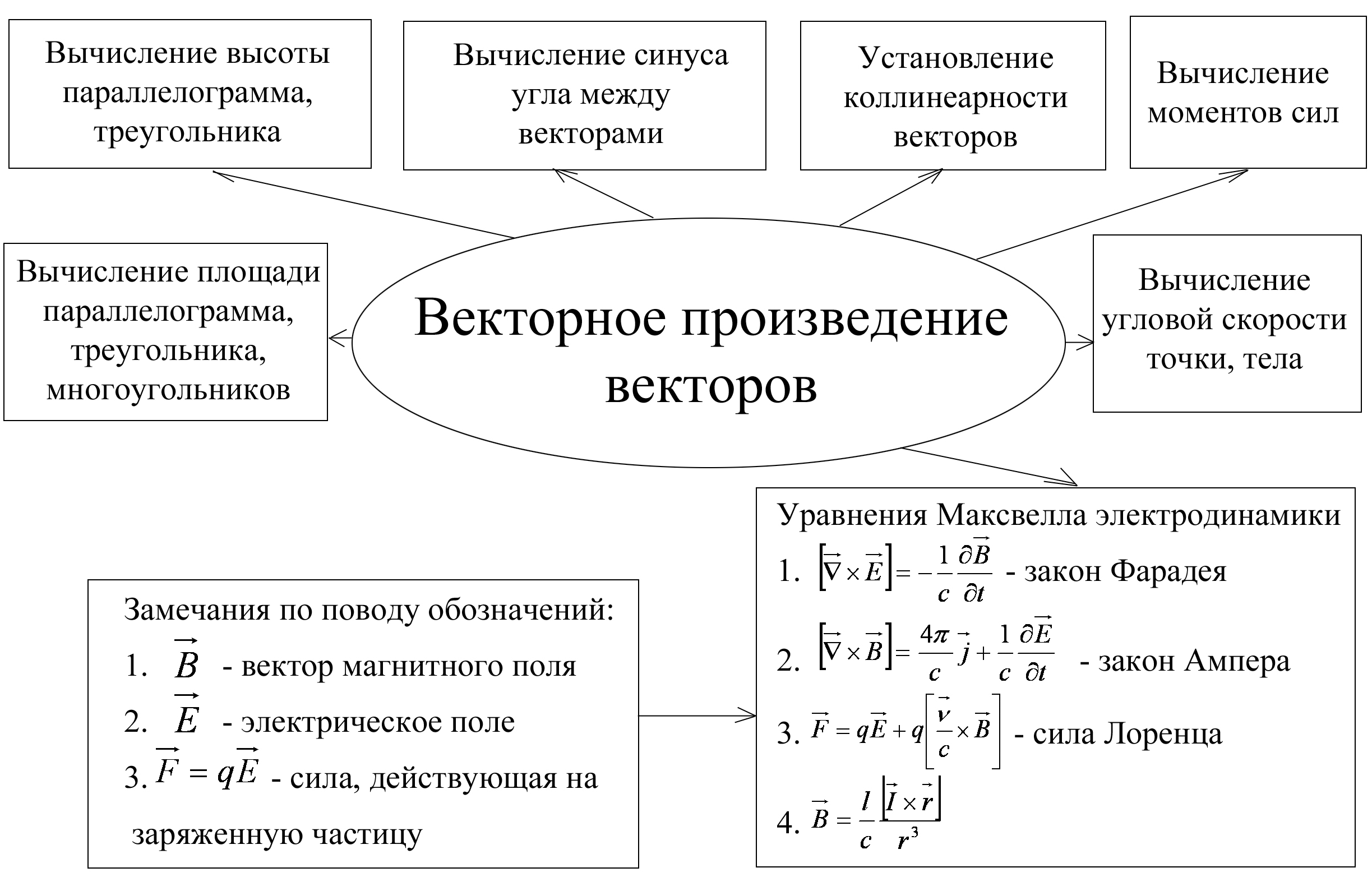
2.5.3. Смешенное произведение трех векторов

Схема 10

Приложения смешанного произведения

Схема 11

2.5.4. Двойное векторное произведение

Схема 12

В качестве упражнения предлагаем указанные свойства доказать самостоятельно.

2.6. Применение векторов в аналитической геометрии. Задачи

Простейшие геометрические задачи, на базе которых решаются задачи более содержательные и значимые, приведены на схеме 13. Каждая её строка содержит некоторый геометрический факт и его запись с помощью векторов. Получить эту запись, используя геометрические свойства заданных объектов, читателю предлагается самостоятельно. При этом он может использовать и любой учебник по аналитической геометрии.

Замечания

1. Утверждения 1, 2 лежат в основе вывода уравнений прямой линии как на плоскости, так и в пространстве.

2. Утверждения 9 и 10 лежат в основе вывода уравнений плоскости.

3. Утверждение 11 позволяет получить уравнение прямой линии на плоскости по точке и нормальному вектору.

Решение следующих задач требует знания определения уравнения множества точек относительно заданной системы координат.

Уравнением множества точек (на плоскости или в пространстве) относительно заданной системы координат называется уравнение или неравенство, которому удовлетворяют координаты любой точки этого множества, но не удовлетворяют координаты точек, которые этому множеству не принадлежат. Заметим, что множество может быть описано не одним, а несколькими уравнениями или неравенствами.

Схема 13

Используя это понятие, решите следующие задачи:

15. Написать уравнение прямой заданной точкой и вектором который является направляющим для т.е. удовлетворяет условию

16. Решить эту же задачу, если т.е. если рассматривается прямая в пространстве.

17. Написать уравнение прямой лежащей в плоскости, если известна одна ее точка и вектор

18. Написать уравнение прямой по двум ее точкам и в случаях:

а) если т.е лежит в плоскости;

б) если т.е. если лежит в пространстве.

19. Написать уравнение плоскости, если известно:

а) что она проходит через точку параллельно векторам и

б) она проходит через три точки:

в) она проходит через точку перпендикулярно к вектору

Задачи, решаемые с использованием скалярного, векторного и смешанного произведений

Из определения и свойств скалярного произведения следует:

1.

2. ;

3.

4.

5. Если то где  – углы, которые составляют вектор с базисными векторами

Из определения и свойств векторного произведения следует:

1.

2. Если и при некотором

3.

Из свойств смешанного произведения трех векторов заключаем:

1. , ,  – правая тройка, если

, ,  – левая тройка, если

2. , ,  – компланарны

3.  – параллелепипед;

 – треугольная призма;

– треугольная пирамида.

20. Даны вершины треугольника: Определить его внутренний и внешний углы при вершине

21. Доказать, что треугольник где равнобедренный. Вычислить его внутренние и внешние углы.

22. Найти проекцию вектора на ось, составляющую с координатными осями равные острые углы.

23. Найти проекцию вектора на ось, составляющую с координатными осями и углы и а с осью – острый угол

24. .Даны две точки Найти проекцию вектора на ось, составляющую с координатными осями и углы и а с осью – тупой угол

25. Вычислить проекцию вектора на ось вектора

26. Даны три вектора: и Вычислить скалярную проекцию вектора на ось вектора

27. Даны три вектора и Вычислить скалярную проекцию вектора на ось вектора

28. Даны три вектора и Вычислить скалярную проекцию вектора на ось вектора

29. Даны две точки Вычислить проекцию вектора на ось вектора

30. Даны точки Вычислить проекцию вектора на ось вектора

31. Вычислить площадь треугольника если

32. Даны вершины треугольника: Вычислить длину его высоты, опущенной из вершины

33. Вычислить синус угла между векторами и

34. Определить, какой является тройка векторов (правой или левой), если

1) 2) 3)

4) 5) 6)

35. Установить, компланарны ли векторы если

1) 

2) 

3)

36. Доказать, что четыре точки лежат в одной плоскости.

37. Вычислить объем тетраэдра, вершины которого находятся в точках

38. Даны вершины тетраэдра: Вычислить длину его высоты, опущенной из вершины

39. Объем тетраэдра равен три его вершины находятся в точках Найти четвертую вершину если известно, что она лежит на оси