4.3.2. Специальные виды векторных полей – потенциальное и соленоидальное
Поле называется потенциальным, если
оно является полем градиента некоторого
скалярного поля. Иначе, поле
потенциально, если существует скалярное
поле U, такое что
Функция U называется потенциалом поля
Критерием потенциальности поля
является равенство нулю вихря:
Если
потенциально, то
т.е. интеграл
не зависит от пути интегрирования и
равен разности потенциалов между
конечной точкой кривой и ее начальной
точкой.
Задача 37. Найти потенциал поля
Решение. Убедимся в его потенциальности,
и если оно потенциально, то криволинейный
интеграл
не зависит от пути интегрирования, а
зависит лишь от начальной
и конечной её точки В. Итак,
Тогда разность потенциалов
где
Соединим точки А и В ломаной:
Тогда
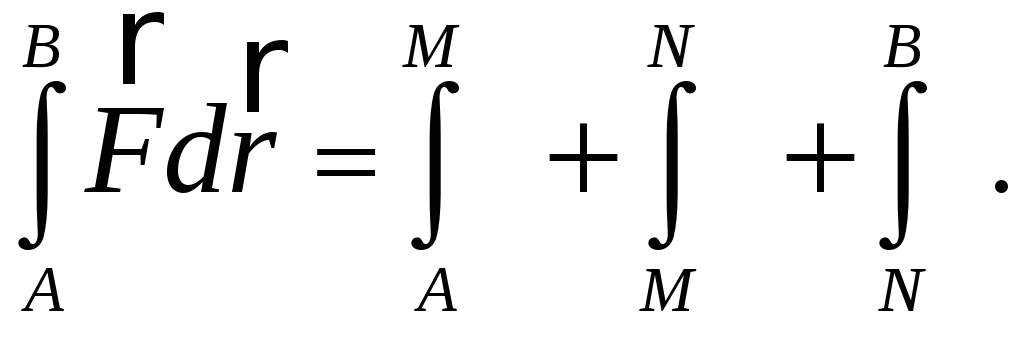Найдём каждое из слагаемых:
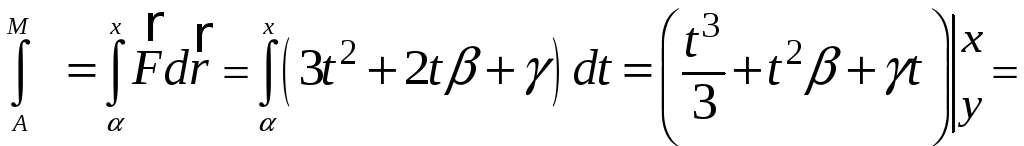
Искомый интеграл будет равен
Поэтому
Задачи для самостоятельного решения: [4, с. 173–174; 5, с. 247 задачи № 55, 57, 59; 10, с. 108].
Поле, в котором дивергенция равна нулю, называется соленоидальным. Векторные линии поля (кривые, касающиеся поля в каждой своей точке) не могут начинаться или заканчиваться в области соленоидальности; это может происходить лишь на границе этой области, либо эти кривые замкнуты. В соленоидальном поле поток вектора через поперечное сечение векторной трубки сохраняет постоянное значение, что следует из теоремы Остроградского – Гаусса.
Задачи для самостоятельного решения: [4, с. 175; 10, с. 123–125].
4.3.3. Некоторые физические задачи из теории поля
Задача 38 (10, с. 18, пр. 3])
Электрический ток силы I
течет по бесконечному проводу вдоль
оси
Найти напряженность
магнитного поля, создаваемого этим
проводом в произвольной точке
пространства.
Решение. По закону Био-Савара
Здесь
– напряженность магнитного поля,
создаваемого током в произвольной точке
M пространства. Элемент тока
определяется значением
на
вектором
и
величиной I (в точке
);
вектор
идет из точки
в M. Если
–
единичный вектор, сонаправленный с осью
–
с осью
–
с осью
то
Тогда
Поэтому
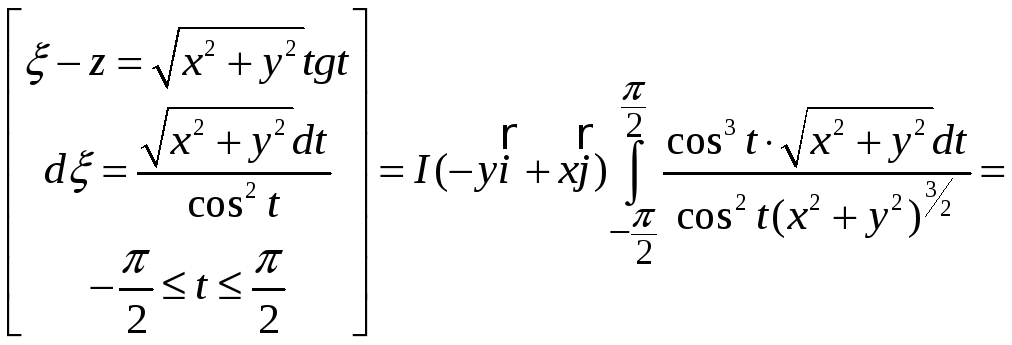
Таким образом,
где
–
расстояние от точки М до оси
Задача 39. Установить является ли
поле
из задачи потенциальным, и в случае
положительного ответа на этот вопрос,
найти его потенциал.
Решение. Для потенциальности поля
достаточно установить равенство
Таким образом, поле
потенциально всюду за исключением точек
оси
т.е. самого проводника.
Найдем потенциал
поля
т.е. такую функцию
для которой
Поскольку
то криволинейный интеграл
не зависит от пути интегрирования, а
зависит лишь от начальной точки
и конечной точки
Проинтегрируем вдоль ломаной
,
у которой
Тогда
где
Найдём каждый из интегралов, стоящий в
правой части равенства:
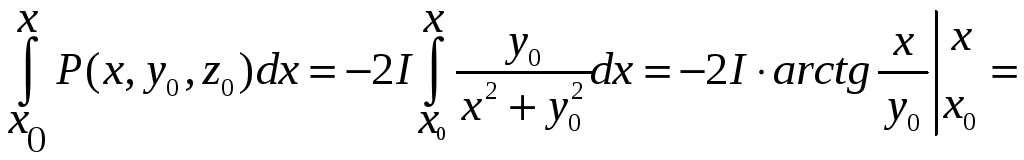
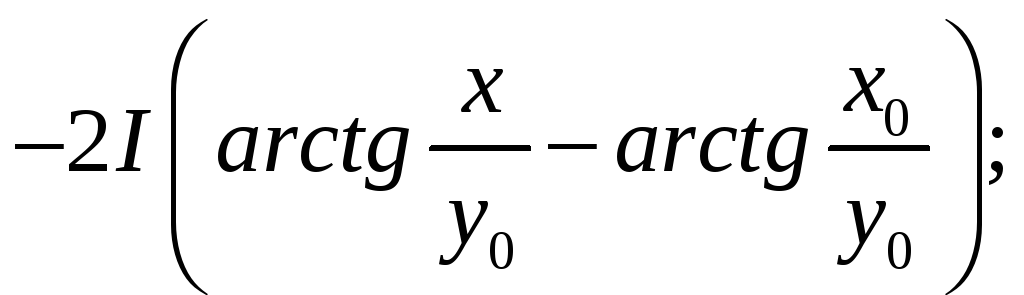
Таким образом,
где
В самом деле,
Итак,
Для проверки вычислим grad φ:
Задача 40. Выяснить, является ли
поле
соленоидальным. Если да, то найти его
векторный потенциал.
Решение. Для соленоидальности поля
достаточно
установить равенство
т.е. равенство
что получается мгновенно:
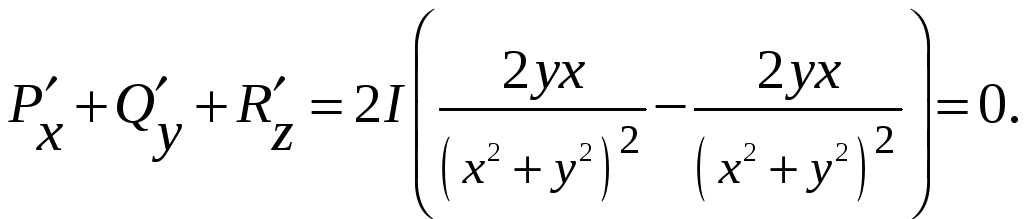Таким образом, поле
соленоидально всюду, за исключением
оси
Найдем новое поле
,
такое что
или, что равносильно,
из этих равенств имеем:
Для нахождения всех решений
достаточно найти одно, поскольку
где
– любая функция от
ибо всегда
Поэтому, полагая
,
найдем
откуда
Поэтому
Проверим равенство
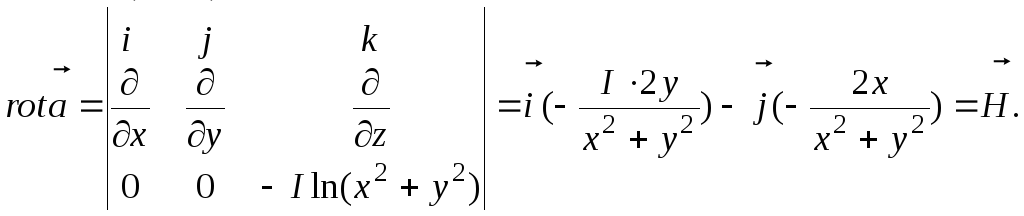
Поэтому
где f – любая непрерывно
дифференцируемая функция переменных
.
Задача 41.
Найти векторные линии поля
.
Решение. Уравнение векторной линии:
Поскольку
то
т.е.
Далее,
Отсюда
что означает
т.е.
Таким образом, векторные линии суть
окружности
Задача 42.
Вычислить циркуляцию
векторного поля
вдоль окружности
Решение.
Отличность от нуля циркуляции поля
вдоль
объясняется наличием особой точки
вектор-функции
внутри контура ω. Число
носит название циклической постоянной
относительно особой точки
Значение циклической постоянной не
зависит от контура
содержащего внутри себя эту точку.
Заметим, что если контур
не содержит внутри себя точку
,
то
