1. Системы линейных уравнений

Тема «Системы линейных уравнений» является основополагающей при изучении курса «Линейная алгебра и аналитическая геометрия». К решению системы линейных уравнений приводят многие задачи этого курса, а также других математических дисциплин.

Логические связи темы «Системы линейных уравнений» с другими темами учебной дисциплины демонстрирует схема 1. Эта схема является своеобразным опорным сигналом, позволяющим осознать важность темы и её место в изучаемом курсе.

Схема 1

Некоторое представление о преимуществах теории систем линейных уравнений в других областях знаний дает следующая схема

Схема 2

Ниже будут рассмотрены некоторые прикладные задачи, приводящие к решению системы линейных уравнений. Но сначала мы приведем справочный материал по теме.

1.1. Понятие системы линейных уравнений и её решения

Определение 1. Системой линейных уравнений с переменными называется система вида

(1)

где - заданные числа.

Определение 2. Решением системы линейных уравнений называется упорядоченный набор чисел при подстановке которых в систему вместо переменных каждое из её уравнений обращается в верное числовое равенство.

1.2. Виды систем линейных уравнений

Классификация систем по множеству решений.

Решить систему – это значит найти все её решения или доказать, что решений нет.

Виды записи систем линейных уравнений.

1.3. Методы решений системы

1.3.1. Комментарии к методу Гаусса

Этот метод впервые был описан К. Гауссом (1777 – 1855) в 1849 году¹. Однако следует заметить, что прием решения системы из n линейных уравнений с n переменными по существу совпадающий с методом Гаусса, был разработан в Древнем Китае ещё до нашей эры. Он изложен в восьмой книге анонимной древнекитайской «Математики в девяти книгах» и назван правилом «Фан-чэн». Своеобразие правила «Фан-чэн» составляет техника вычислений, приводившихся на специальной счетной доске².

В основе метода Гаусса лежат элементарные преобразования системы.

Замечания:

1. Здесь , так как в процессе преобразований уравнения вида вычеркиваются.

2. Если в процессе преобразований системы появляется уравнение , то система решений не имеет.

3. Система (2) называется системой, приведенной к разрешимому виду.

1.3.2. Комментарии к методу Жордана – Гаусса

Метод Жордана – Гаусса отличается от метода Гаусса лишь тем, что вычисление коэффициентов системы, которая получается после исключения какой-то переменной из всех уравнений, кроме одного, производится по определенному правилу – правилу Жордана – Гаусса.

Пусть в матрице коэффициентов системы . Тогда исключим переменную из всех уравнений

,

кроме уравнения с номером р:

Для этого уравнение с номером p разделим на умножим на и сложим с уравнением, номер которого i. В результате получим правило пересчета коэффициентов системы:

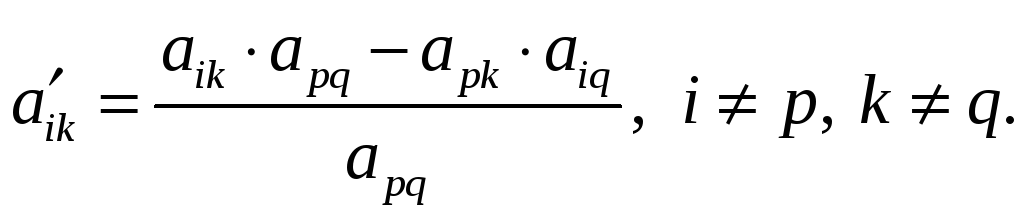
Расчет по последней формуле удобно производить, пользуясь мнемоническим «правилом прямоугольника», наглядно показанным на рисунке 1.

Заменяемый эл-т
				i-ая строка
		+ -
				p-ая строка
	k-ый столбец		q-ый столбец	Разрешающий эл-т

Рис. 1