4.2.4. Физические приложения поверхностного интеграла II рода
Физический смысл поверхностного
интеграла второго рода – поток векторного
поля
в направлении нормали
к поверхности :
В частности, если
–
скорость течения жидкости (тепла) в
точке M, то
представляет собой поток жидкости
(тепла) через выбранную сторону
поверхности.
4.3. Некоторые соотношения между характеристиками скалярных и векторных полей
4.3.1. Основные характеристики полей
Дивергенция векторного поля
в данной точке М определяется как
предел отношения его потока через
замкнутую поверхность σ, содержащую
внутри себя точку М, в направлении
внешней нормали, к объему v
тела Ω, границей которого служит
поверхность σ, при условии, что
:
Дивергенция
в точке M характеризует
«мощность источника» M
(если она положительна) и «мощность
стока» M (если она
отрицательна). В декартовых координатах
это скалярное поле выражается формулой:
здесь
Имеет место формула Остроградского – Гаусса
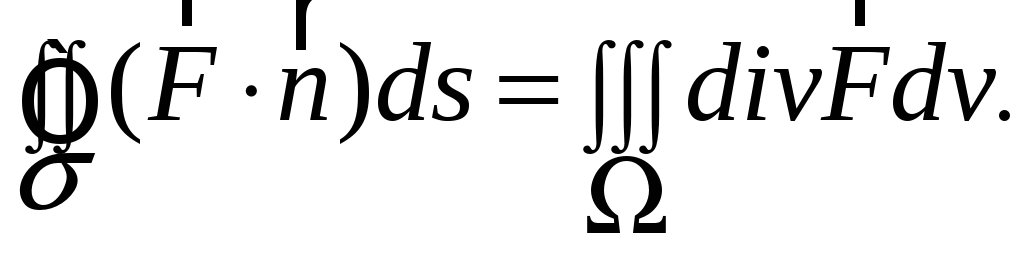
В этой формуле поток Π в левой части
равенства вычисляется для замкнутой
поверхности σ в направлении внешней
нормали к ней, тройной интеграл в правой
части равенства вычисляется по телу Ω,
границей которого служит поверхность
σ. В более подробной записи правая часть
приобретает вид: Π =
Задача 30.
Найти поток векторного поля
через всю поверхность цилиндра,
ограниченного поверхностями:
в направлении внешней нормали.
Решение.
Задачи для самостоятельного решения: [5, с. 196–197; 10, с. 79–80; 4, с. 166 (без 3.8)].
Ротор векторного поля
обозначаемый символом
есть новое векторное поле, которое
строится следующим образом: его
ортогональная проекция на произвольный
единичный вектор
вычисляется по формуле:
Здесь
–
произвольный замкнутый контур, лежащий
в плоскости, перпендикулярной вектору
который обходится против часовой
стрелки, если смотреть из конца вектора
содержит внутри себя точку М, S –
площадь фигуры, ограниченной контуром
В декартовых прямоугольных координатах
имеет вид:
Здесь поле
имеет координаты
Ротор
характеризует завихренность поля
в данной точке.
Задача 31. Найти поток векторного
поля
через сферу
в направлении внешней нормали.
Решение.
Задача 32. Найти поток векторного
поля
через замкнутую поверхность
в направлении внешней нормали двумя
способами: а) непосредственно, б) по
теореме Остроградского – Гаусса.
Решение. а)
Для
найдем
Т.к.
то
Поэтому
б)
=
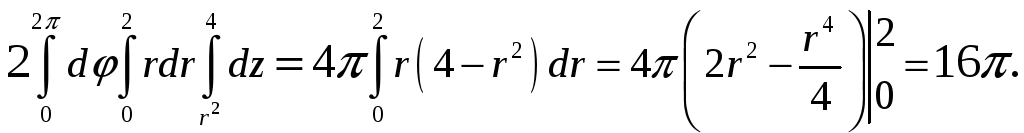
Задача 33. Поле с нулевой дивергенцией называется соленоидальным. Выяснить, какие из следующих полей соленоидальны:
а)
(да)
б)
(нет)
в)
(да)
Задача 34. Найти дивергенцию векторного
поля
где
–
постоянный вектор,
Решение.
Задача 35. Электростатическое поле
точечного заряда q равно
Вычислить
Решение.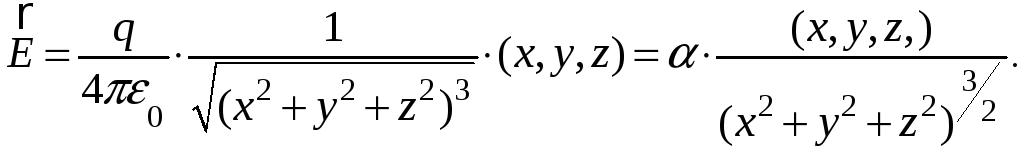 
Очевидно, что
ибо
поэтому
Далее, векторное поле
характеризует зависимость поля
В самом деле, рассмотрим вращение
твердого тела вокруг оси
с угловой скоростью
тогда линейная скорость
точки
этого
тела представима в виде:
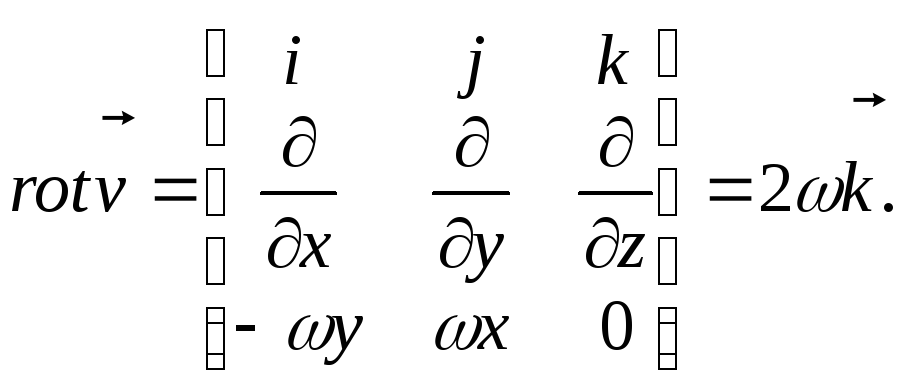
Т.е.
сонаправлен с осью вращения
его модуль равен удвоенной угловой
скорости вращения тела и не зависит от
точки М.
Теорема Стокса. Циркуляция
векторного поля
по произвольному кусочно-гладкому
замкнутому контуру
равна потоку векторного поля
через поверхность
границей которого служит
Обход контура против часовой стрелки,
если смотреть из конца вектора
-нормали
к поверхности
Задача 36. Вычислить циркуляцию С
векторного поля
по окружности
в положительном направлении относительно
вектора
Решение. а) Непосредственно.
б) По теореме Стокса.
Здесь
–
круг
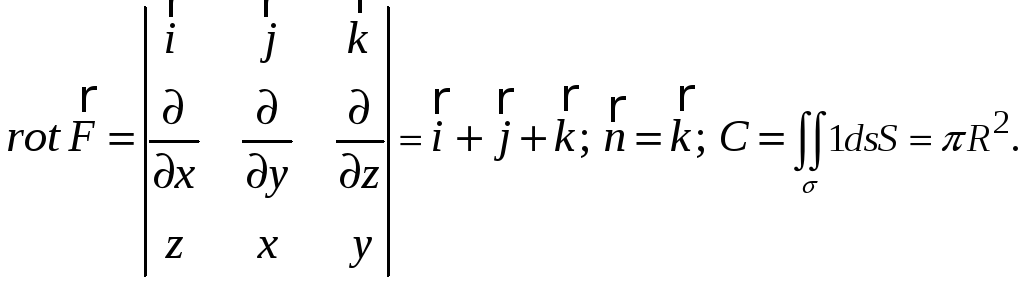
в) По теореме Стокса.
–
полусфера
Найдем
Поскольку
то
Поэтому
В полярных координатах
Рассмотренный выше пример служит
подтверждением теоремы Стокса в той ее
части, которая касается произвольности
поверхности ,
границей которой служит заданный контур
Задачи для самостоятельного решения: [4, с. 168–169; 5, с. 246–247 задачи № 50 – 54; 10, с. 90–96].