4.1.4. Физические приложения криволинейного интеграла II рода

а) Вычисление работы силы при перемещении материальной из точки А массы 1 в точку В вдоль дуги кривой (если  – плоское), (если  – пространственная кривая).

б) Если  – скорость плоского потока жидкости в точке то количество жидкости, вытекающей за единицу времени из области равно где  – единичный вектор к внешней нормали к кривой в точке Если направление касательного вектора к соответствует положительному направлению обхода кривой и то и

в) Вычисление магнитной индукции магнитного поля, создаваемого током протекающим по замкнутому проводнику в точке ([5 с. 144–145]).

Задача 18. Вычислить работу силового поля вдоль дуги эллипса обходя контур против часовой стрелки.

Решение. поэтому

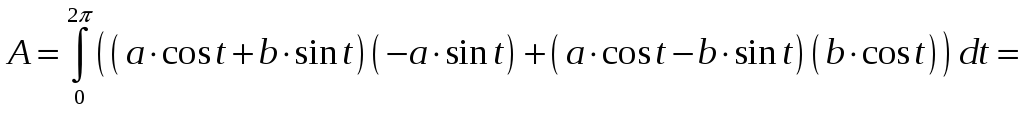
Ответ: 0. На самом деле, это верно для любого гладкого замкнутого контура

Задача 19. Найти работу силы при перемещении материальной точки вдоль дуги из точки до точки Как изменится ответ, если  – отрезок

Решение. Параметризуем поэтому

Ответ:

Пусть , тогда

Задача 20. Найти циркуляцию векторного поля вдоль

Решение:

4.2. Поверхностные интегралы и их физические приложения

4.2.1. Поверхностный интеграл I рода

Замечание. Если то  – площадь поверхности

Более точные определения можно найти, например, в [5, с. 160–168].

Задача 21. Вычислить площадь гиперболического параболоида вырезанного цилиндром

Решение: Перейдём к полярным координатам в плоскости Тогда

4.2.2. Физические приложения поверхностного интеграла I рода

Если  – плотность материальной поверхности, то с помощью поверхностных интегралов I рода вычисляются следующие физические величины:

а)  – масса поверхности

b)  – статический момент поверхности относительно плоскости Аналогично определены моменты и

c) Координаты центра масс поверхности:

d)  – момент инерции поверхности относительно оси

e)  – момент инерции поверхности относительно плоскости

f) - момент инерции поверхности относительно начала координат.

Задача 22. Для гиперболического параболоида вырезанного цилиндром найти все параметры, перечисленные в пунктах a) – c), и найти и из d) – f) соответственно.

Решение: a) масса куска поверхности  – плотность:

что следует из решения задачи 21.

b)

Вновь перейдем к полярным координатам :

Тогда

ибо

Отсюда следует, что центр масс поверхности находится в точке

d)

e)

f) .

Каждое из слагаемых нами уже найдено в пунктах d) и e) соответственно.

Задача 23. Найти значение параметров и пунктов a) – f), для однородной полусферы плотности

Задачи для самостоятельного решения: [5, с. 172–173; 4, с. 158].

4.2.3. Поверхностный интеграл II рода

Способы вычисления потока векторного поля зависят от задания поверхности Возможный три случая.

1) В этом случает поверхность однозначно проектируется на плоскость и

Здесь  – угол между и Нормаль находится по формуле: причем знак “+” выбирается в том случае, если нормаль и образуют острый угол, в противном случае – “–”.

Задача 24: 1. Найти поток векторного поля через верхнюю сторону поверхности , ограниченную

Рис. 1

Решение. Здесь поэтому

т.к. следовательно

Поэтому

И, следовательно ибо – четверть круга радиуса

2) Поверхность задана неявным уравнением

В этой ситуации вектор нормали может быть вычислен по формуле:

Здесь Выбор знака в выражении для вектора нормали осуществляется в соответствии со стороной поверхности

Задача 25. Найти поток П векторного поля через сферу в направлении внешней нормали Т.к. в точке вектор то

Замечание. Для замкнутой поверхности имеет место формулы Остроградского – Гаусса: Здесь  – трёхмерное тело, границей которого служит Итак, поток П для предыдущего примера:

c) Поверхность биективно проектируется на все три координатные плоскости: области  – суть проекции поверхности на плоскости (Oxy), (Oxz) и (Oyz), соответственно. В такой ситуации

,

здесь знаки перед первым, вторым и третьим интегралом равны соответственно знакам скалярных произведения и или, что равносильно, знакам чисел и . Соответственно: .

Задача 26. Найти поток векторного поля через внешнюю сторону части сферы расположенную в 1-м октанте.

Здесь причем , поэтому

Задачи для самостоятельного решения: [5, с. 180–181; 10, с. 64, 69; 4, с. 164–165].

Задача 27. Найти поток П векторного поля через часть параболоида отсеченную плоскостью в направлении к внешней по отношению к параболоиду нормали.

Решение:

=> берём “–” т.е.: поэтому Перейдём к полярным координатам

Задача 28. Найти поток П векторного поля через замкнутую поверхность в направлении внешней нормали

Рис. 2

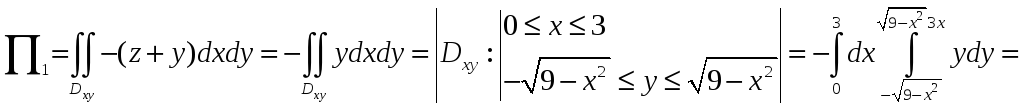
Проекция на плоскость (Oyz) поверхности  – полукруг (см. рис. 3).

Рис. 3

 – полукруг

Найдем

и т.к. , то берём с “+”! => ;

Найдём Проекция поверхности на плоскость Оyz-полукруг

Рис. 4

Найдем . Поскольку , то поэтому А поскольку , то

Поэтому

С другой стороны, поскольку поверхность замкнута, то можно применить теорему Остроградского – Гаусса.

Опишем  поэтому

Задача 29. Найти поток П векторного поля через часть поверхности расположенную в 1-м октанте. Нормаль к ней образует острый угол с осью

Решение.

Итак, Поскольку и то Π=+ + = +2 + 2. Поскольку то

+

При вычислении интегралов были сделаны следующие замены:

Другой способ. Замкнем поверхность до поверхности пирамиды: По теореме Остроградского – Гаусса

ибо

Π₃== ибо х = 0.

Поэтому