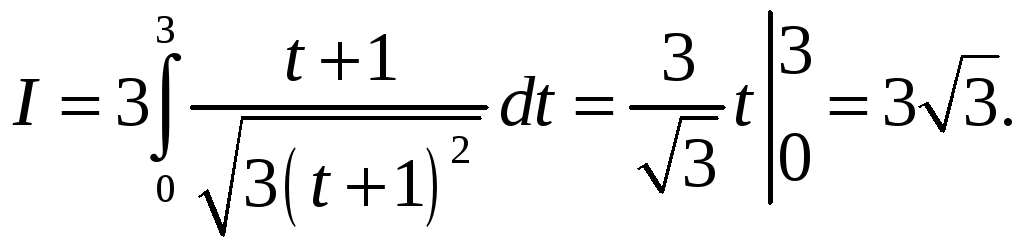- •Математика для студентов в задачах и упражнениях по физике
- •1. Системы линейных уравнений
- •1.3.2. Комментарии к методу Жордана – Гаусса
- •1.4. Однородная система линейных уравнений
- •1.5. Применение теории систем линейных уравнений
- •1.5.1. Применение в аналитической геометрии
- •1.5.2. Расчет электрических цепей
- •1.5.3. Расчет потоков транспорта на развилках дорог
- •1.5.4. Описание системы сил, действующих на упругую статическую систему s закрепленную на краях
- •1.5.5. Применение метода наименьших квадратов для обработки результатов измерений
- •1.6. Учебная литература
- •2. Векторная алгебра и её приложения
- •2.1. Понятие вектора. Линейные операции над векторами
- •2.2. Линейная зависимость векторов. Базис системы векторов
- •2.3. Понятие системы координат. Координаты точки
- •2.4. Задачи и упражнения
- •2.7. Физические приложения векторной алгебры
- •2.7.1. Равнодействующая сил. Теорема сложения скоростей
- •2.7.2. Простейшие задачи статики
- •2.7.3. Центр масс системы материальных точек
- •2.7.4. Вычисление работы, моментов инерции и угловых скоростей
- •2.7.5. Уравнение траектории движущейся точки
- •2.8. Учебная литература
- •3. Векторное описание канала связи
- •3.1. Построение ансамбля сигналов размерности 2
- •3.2. Построение многомерных сигналов
- •3.3. Процедура детектирования сигналов
- •4. Векторный анализ
- •4.1. Криволинейные интегралы и их физические приложения
- •4.1.1 Криволинейный интеграл I рода от скалярной функции вдоль кривой
- •4.1.2. Физические приложения криволинейного интеграла I рода
- •4.1.3. Криволинейный интеграл II рода
- •4.1.4. Физические приложения криволинейного интеграла II рода
- •4.2. Поверхностные интегралы и их физические приложения
- •4.2.1. Поверхностный интеграл I рода
- •4.2.2. Физические приложения поверхностного интеграла I рода
- •4.2.3. Поверхностный интеграл II рода
- •4.2.4. Физические приложения поверхностного интеграла II рода
- •4.3. Некоторые соотношения между характеристиками скалярных и векторных полей
- •4.3.1. Основные характеристики полей
- •4.3.2. Специальные виды векторных полей – потенциальное и соленоидальное
- •4.3.3. Некоторые физические задачи из теории поля
- •4.4. Учебная литература
- •Ответы и указания Глава 1
- •Глава 2
- •Глава 3
- •Глава 4
- •Содержание
- •1. Системы линейных уравнений 5
- •2. Векторная алгебра и её приложения 30
- •3. Векторное описание канала связи 75
- •4. Векторный анализ 91
- •Математика для студентов в задачах и упражнениях по физике
- •150000 Ярославль, ул. Советская, 14.
4.1.2. Физические приложения криволинейного интеграла I рода
a) Вычисление массы плоской
материальной кривой
![]() с линейной плотностью
с линейной плотностью
![]()
 –
масса кривой
–
масса кривой
![]() с плотностью
с плотностью
![]()
b) Вычисление статических
моментов
![]() относительно осей
относительно осей
![]() и
и
![]() соответственно:
соответственно:


c) Определение моментов
инерции кривой
![]() относительно осей
относительно осей
![]() и
и
![]() соответственно
соответственно
![]()
![]()
d) Определение момента
инерции кривой относительно начала
координат

e) Определение моментов
инерции кривой
![]() относительно осей
относительно осей
![]() и
и
![]() соответственно
соответственно


Приведенные выше формулы a)-e) имеют естественное обобщение на трехмерное пространство:
Если
![]() –
пространственная кривая и
–
пространственная кривая и
![]() –
линейная плотность, то формулы для
вычисления соответствующих физических
величин будут выглядеть следующим
образом:
–
линейная плотность, то формулы для
вычисления соответствующих физических
величин будут выглядеть следующим
образом:
a) Вычисление массы

b) Вычисление статических
моментов относительно координатных
плоскостей



c) Определение координат
центра масс кривой
![]()
![]()
![]()
d) Определение момента
инерции кривой относительно начала
координат

e) Вычисление моментов
инерции кривой
![]() относительно осей координат (моменты
2-го порядка)
относительно осей координат (моменты
2-го порядка)


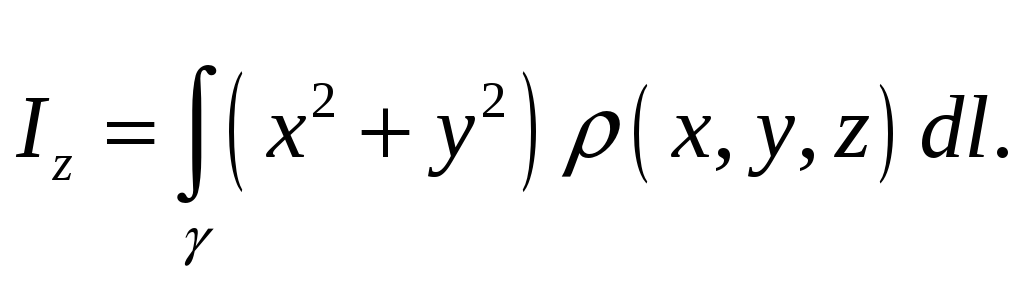
Согласно определению статического момента кривой относительно прямой, статические моменты кривой относительно координатных осей будут вычисляться по формулам:
![]()
![]()
![]()
Вычислим указанные выше параметры a)-e)
для одного витка
![]() -спирали,
намотанной на цилиндр радиуса R
с шагом
-спирали,
намотанной на цилиндр радиуса R
с шагом
![]()
Задача 1. Вычислить значение параметров
![]() определенных в пункте а) из 1, если кривая
определенных в пункте а) из 1, если кривая
![]() определена соотношениями:
определена соотношениями:
![]()
![]()
![]()
![]() а плотность
а плотность
![]() постоянна вдоль кривой.
постоянна вдоль кривой.
Решение: а)
 спирали, намотанной на цилиндр
спирали, намотанной на цилиндр
b)



![]()
с)
![]()
![]()
![]() Таким образом, центр тяжести
Таким образом, центр тяжести
![]() имеет координаты
имеет координаты
![]() Заметим, что
Заметим, что
![]()
d)

![]()
e)
![]()
![]()
![]()
![]()
Легко видеть, что
![]()
Задача 2. Вычислить значение всех
параметров из пунктов a)-e)
раздела 1 для прямолинейного отрезка
![]() плотности
плотности
![]()
![]()
![]()
Решение.
a)
 .
Параметризуем
.
Параметризуем

![]()

b)



c)
![]()
![]()
![]()
d)

e)
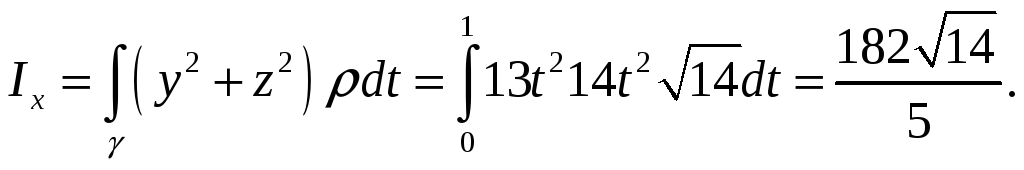


Очевидно, что
![]()
Задача 3. Найти статический момент
![]() и момент инерции
и момент инерции
![]() дуги астроиды
дуги астроиды
![]() с линейной плотностью
с линейной плотностью
![]()
Решение. Параметризуем дугу
 полагая, что
полагая, что
![]()
Тогда
![]()


Криволинейный интеграл I
рода позволяет вычислить силу притяжения
материальной точки
![]() массы
массы
![]() материальной кривой
материальной кривой
![]()
Задача 4. Найти проекцию на оси
координат силы, с которой материальная
однородная дуга окружности
![]() массы
массы
![]() притягивает материальную точку
притягивает материальную точку
![]() массы
массы
![]()
Решение. Координаты проекции
![]() силы
силы
![]() вычисляются по формуле:
вычисляются по формуле:
![]()
![]() где
где
![]() –
гравитационная постоянная,
–
гравитационная постоянная,
![]()
![]() –
угол между
–
угол между
![]() и
и
![]() Очевидно, что
Очевидно, что
![]() Плотность
Плотность
![]()
![]()
![]()
![]()
![]()
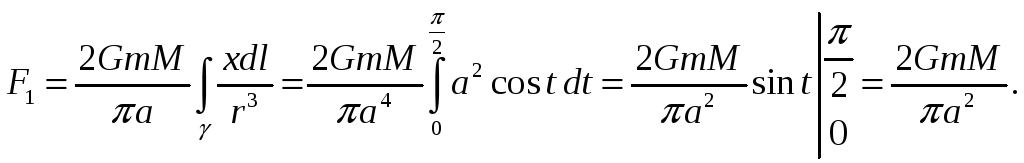

Таким образом,
![]()
Решить самостоятельно следующие задачи.
5. Найти массу и центр тяжести материальной
кривой
![]() с линейной плотностью
с линейной плотностью
![]() если
если
![]()
6. Найти координаты центра тяжести
контура однородного сферического
треугольника:
![]()
Поверхностью уровня функции
![]() называется множество точек
называется множество точек
![]() в
в
![]() таких, что
таких, что
![]() для некоторого
для некоторого
![]()
7. Найти поверхности уровня скалярного
поля
![]()
8. Найти поверхности уровня функции
![]() где
где
![]() –
фиксированный вектор
–
фиксированный вектор
![]()
![]()
9. Найти поверхности уровня функции
![]()
![]()
10. Найти поверхности уровня функции
![]() где
где
![]()
4.1.3. Криволинейный интеграл II рода
Криволинейный интеграл 2-го рода
определяется для векторного поля
![]() вдоль кривой
вдоль кривой
![]()

Физический смысл этого выражения –
работа силы
![]() вдоль пути
вдоль пути
![]() на отрезке
на отрезке
![]()
Формула Грина:
![]()
Здесь
![]() –
замкнутый контур, ограничивающий область
D, направление обхода
контура таково, что область D
остается слева.
–
замкнутый контур, ограничивающий область
D, направление обхода
контура таково, что область D
остается слева.
Задача 11. Вычислить работу A
переменной силы
![]() а) вдоль первого витка спирали
а) вдоль первого витка спирали
![]() б) вдоль отрезка
б) вдоль отрезка
![]() где
где
![]()
![]() в) вдоль ломаной
в) вдоль ломаной
![]()
Решение: а)

б) параметризация отрезка
![]() такова:
такова:
![]()

в)


![]()

Т.е. работа зависит от формы пути, поэтому
поле
![]() не является потенциальным. Иначе говоря,
не существует такого скалярного поля
не является потенциальным. Иначе говоря,
не существует такого скалярного поля
![]() для которого бы выполнялись одновременно
3 равенства:
для которого бы выполнялись одновременно
3 равенства:
![]()
![]()
![]()
Задачи для самостоятельного решения: [5, с. 146–147]; [10, с. 86–90] или [4, с. 160–161].
12. Вычислить криволинейный
интеграл II рода
![]() по следующим кривым: а)
по следующим кривым: а)
![]() б)
б)
![]() в)
в)
![]() соединяющими точку
соединяющими точку
![]() с точкой
с точкой
![]()
13. Вычислить

14. Вычислить
![]()
15. Вычислить
 где
где
![]() –
пересечение сферы
–
пересечение сферы
![]() с частями координатных плоскостей,
ограничивающих первый октант.
с частями координатных плоскостей,
ограничивающих первый октант.
Задача 16. Используя формулу Грина
вычислить криволинейный интеграл
![]() где
где
![]() –
верхняя полуокружность
–
верхняя полуокружность
![]()
Решение. Положим
![]()
![]() и, следовательно,
и, следовательно,
![]() Поэтому
Поэтому

Задача 17. Вычислить криволинейный
интеграл
![]() где
где
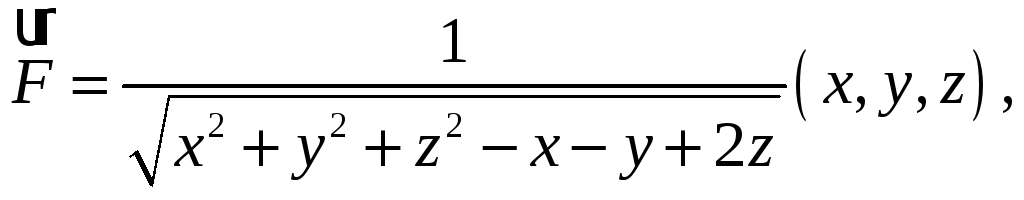
![]()
Решение.
![]()
поэтому