3.3. Процедура детектирования сигналов
Пусть канал связи, как и ранее, описывается уравнением
,
где каждая из компонент
вектора
распределена по нормальному закону с
нулевым математическим ожиданием и
дисперсией
Тогда в силу независимости компонент
плотность вероятностей вектора
равна
Детектирование решает задачу оптимальной
проверки на основе полученного вектора
гипотезы о том, что передано сообщение
Детектор выносит решение
,
если при
условная вероятность
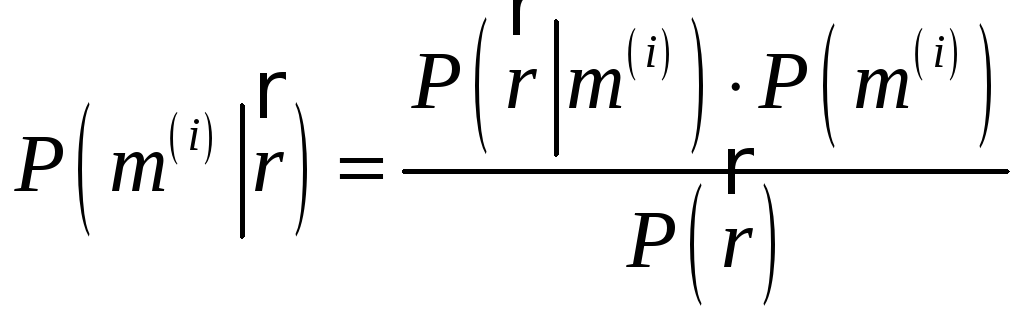является максимальной, при этом
предполагается, что все
равновероятны, т.е.
.
Нахождение максимума функции
при любом
приводит к отысканию
,
где
–
квадрат евклидова расстояния между
принимаемым вектором
и предполагаемым сигналом
Последняя задача приводит к разбиению
на решающие области
–
зоны принятия гипотезы
Таким образом,
Области
носят название областей Воронова.
Рассмотрим задачи на нахождение областей Воронова.
Задача 10. Построить области Воронова
для сигнального созвездия из задачи 2
с параметрами
(рис. 3)
Решение. Срединный перпендикуляр
к отрезку
разбивает плоскость на две полуплоскости:
I и II так, что
Полуплоскость I обладает следующим
характеристическим свойством:
имеет место неравенство
В силу сказанного, для созвездия задачи
2 при
соответствующие области Воронова имеют
вид (см. рис. 7)
На рис. 7 областями Воронова
являются квадранты, полуплоскости и
квадраты, содержащие соответствующие
точки
Например,
–
это «юго-западный» квадрант, содержащий
точку
,
а
–
квадрат с центром в точке
,
–
полуполоса содержащая точку
.
Системы неравенств, описывающие эти
области, имеют вид:
Рис. 7
Задача 11. Найти области Воронова
для сигнальных созвездий задачи 1.1 –
1.5. Написать систему неравенств,
определяющих каждую из областей
.
Заметим, что в том случае, когда точки
сигнального созвездия являются вершинами
правильного многоугольника, вписанного
в окружность (рис. 4), срединные
перпендикуляры к сторонам этого
многоугольника проходят через центр
окружности. Поэтому области Воронова
будут представлять собой углы, содержащие
точку
,
является «соседние» биссектрисы.
Задача 12. Найти области Воронова
для сигнального созвездия задачи 4 при
Записать систему неравенств, определяющих
эти области.
4. Векторный анализ
4.1. Криволинейные интегралы и их физические приложения
При определении криволинейных или поверхностных интегралов предполагается, что соответствующая кривая (поверхность) погружается в скалярное или векторное поле.
4.1.1 Криволинейный интеграл I рода от скалярной функции вдоль кривой
Пусть кривая
задана параметрически:
(1)
где
гладко зависят от параметра t,
а
–
скалярное поле, в котором лежит область
значений отображения (1).
Физический смысл этого выражения достаточно ясен из его обозначения: значение поля U в точке (x,y,z) умножается на длину малого участка кривой, после чего происходит суммирование по этим участкам.
В частности, если
–
линейная плотность проволоки, то интеграл
даёт массу всего участка
Более точные определения можно найти, например [5] или [8]. Там же приведены примеры физических приложений криволинейных интегралов I рода.