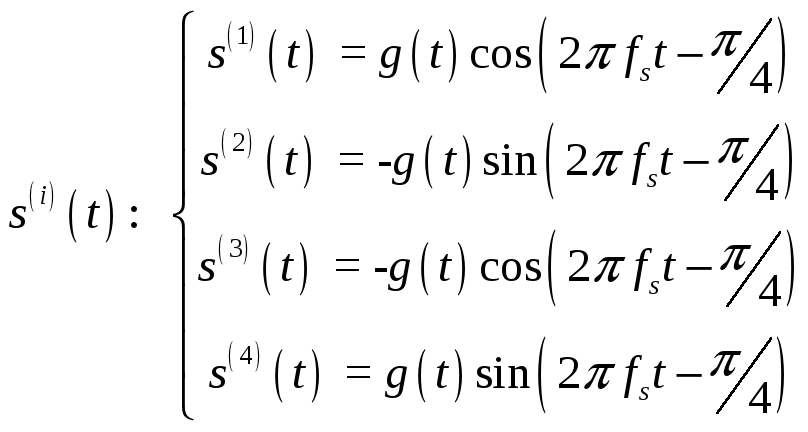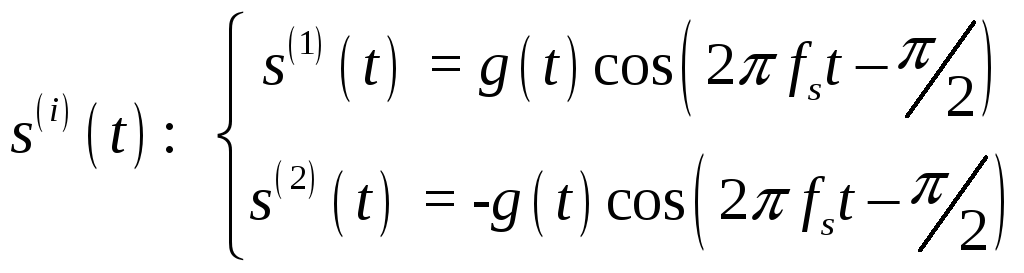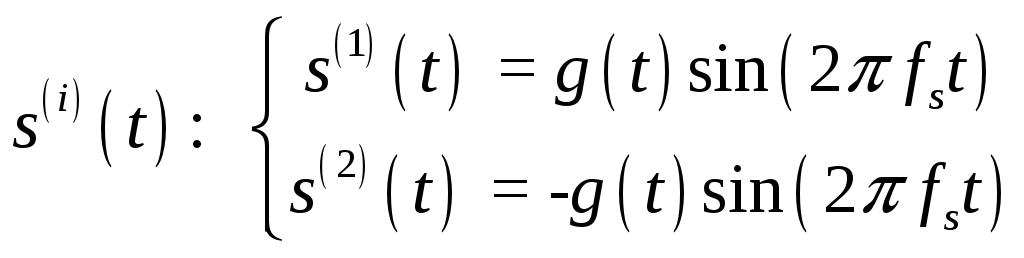2.8. Учебная литература

1. Атанасян, Л.С. Сборник задач по геометрии. Ч. 1 / Л.С. Атанасян, В.А. Атанасян. – М.: Просвещение, 1973. – С. 4–5, 10–11, 18–19, 28, 43–48, 125–126.

2. Беклемишева, Л.А.. Сборник задач по аналитической геометрии и линейной алгебре / Л.А. Беклемишева, А.Ю. Петрович, И.А. Чубаров. – М.: Наука; Гл. ред. физ.-мат. лит., 1987. – с. 160–178.

3. Блехман И.И. Механика и прикладная математика: Логика и особенности приложений математики. / И.И. Блехман, А.Д. Мышкис, Я.Г. Пановко. – 2-е изд. – М.: Наука, 1990, – 356 с.

4. Бухгольц, Н.Н. Основной курс теоретической механики. Ч. 1 / Н.Н. Бухгольц. – М.: Наука, 1967.

5. Веселовский, И.Н. Основания векторной алгебры и ее приложений в геометрии и статике. Гос. технико-теоретическое издательство / И.Н. Веселовский. – М.; Л.: Гос. технико-теоретиче­ское изд-во, 1932. – 132 с.

6. Голубева, О.В. Теоретическая механика / О.В. Голубева. – М. Высшая школа, 1976, – 352 с.

7. Зельдович, Я.Б. Высшая математика для начинающих: Задачи, принципы, методология. / Я.Б. Зельдович. – 5-е изд. – М.: Наука, 1970. – 560 с.

8. Зельдович, Я.Б. Элементы прикладной математики / Я.Б. Зельдович, А.Д. Мышкис. – 3-е изд. – М.: Наука, 1972. – 592 с.

9. Зельдович, Я.Б. Элементы математической физики. Среда из невзаимодействующих частиц / Я.Б. Зельдович, А.Д. Мышкис – М.: Наука, 1973, – 351 с.

10. Ильин, В.А. Линейная алгебра / В.А. Ильин, Э.Г. Поздняк. – М. Наука, 1984, гл. 3, § 1.

11. Коган, В.Ф. О разложении сил и о реакциях связей / В.Ф. Коган. – ВОФЭМ, 1912. – № 576.

12. Канатиков, А.Н. Аналитическая геометрия / А.Н. Канатиков, А.П. Крищенко – М.: МГТУ им. Н.Э. Баумана, 2002. – 312 с.

13. Клетеник Д.В. Сборник задач по аналитической геометрии / Д.В, Клетеник. – М.: Наука, 1986. – С. 123–124, 126–128, 130, 132.

14. Купер Л. Физика для всех: Т. 1. Классическая физика / Л. Купер. – М.: Мир, 1972. – 480 с.

15. Майоров, В.М. Задачник практикум по векторной алгебре (с приложениями к геометрии, элементарной геометрии и статике) / В.М. Майоров, З.А. Скопец. – М.: Учпедизд, 1961. – С. 29–32, 43–50, 127–129.

16. Меркин, Д.Р. Алгебра свободных и скользящих векторов / Д.Р. Меркин. – М.: Физматгиз, 1962. – 164 с.

17. Мышкис, А.Д. Лекции по высшей математике / А.Д. Мышкис. – 4-е изд. – М.: Наука, 1973.  – 640 с.

18. Мышкис, А.Д. Элементы теории математических моделей / А.Д. Мышкис. – М.: Физматлит, 1994. – 194 с.

19. Федорчук, В.В. Курс аналитической геометрии и линейной алгебры. Учеб. пособие / В.В. Федорчук. – М.: Изд-во МГУ, 1990. – С. 14–46, 71–80.

20. Фейнмановские лекции по физике. Задачи и упражнения. М.: Мир, 1957. – С. 31–44.

21. Цубербиллер, О.Н. Задачи и упражнения по аналитической геометрии / О.Н. Цубербиллер. – М.: Наука, 1966. – С. 27–29, 42–50, 71, 72, 79, 80, 207, 211, 224.

3. Векторное описание канала связи

3.1. Построение ансамбля сигналов размерности  2

Понятие векторного пространства и базиса в нем находит применение в процессе передачи сообщений по каналу цифровой связи (см. рис. 1).

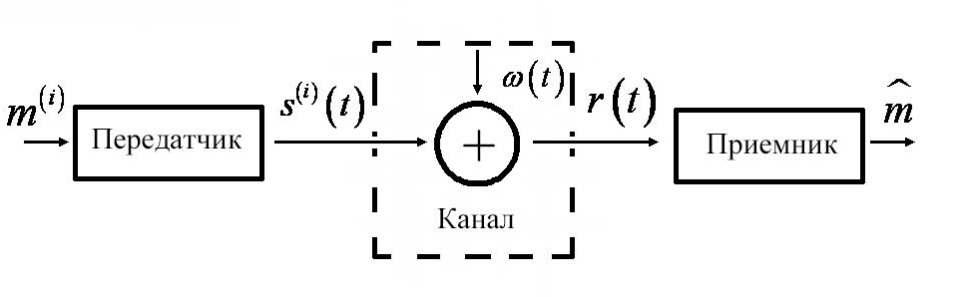
Рис. 1.

Передатчик выбирает одно из возможных сообщений , и передает соответствующий ему сигнал из некоторого множества . В большинстве случаев  – непрерывная функция. Среда передачи называется сигналом. Главной помехой при передаче сигнала является шум . Поэтому в цифровой системе действуют два случайных фактора – сигнал и источник шума. В результате на выходе из канала наблюдается случайный процесс

.

Задача приемника – оценить выбранное сообщение с наилучшей достоверностью. Далее будет рассмотрена векторная модель описания ансамбля сигналов , с помощью которой кодируются сообщения . Ансамбль сигналов есть конечное множество функций , из линейного функционального пространства со скалярным произведением . Линейная оболочка есть конечномерное подпространство в пространстве . Подпространство называется сигнальным пространством. Принято каждый из сигналов представлять в виде линейной комбинации базисных элементов пространства , причем базис , выбирается ортонормированным. Последнее высказывание означает, что

Таким образом, мы приходим к векторной интерпретации передаваемых сигналов: каждый из сигналов представляется n‑мерным вектором в евклидовом пространстве . Соответствующее отображение , в силу однозначности разложения вектора по ортонормированному базису, является изоморфизмом n‑мерных евклидовых пространств. Множество называется сигнальным созвездием. Сигнальное созвездие в случае или принято изображать точками на координатной плоскости. Если ансамбль S содержит n ортогональных векторов , то набор базисных функций получается с помощью нормировки ансамбля S.

Далее предложены задачи для построения сигнального созвездия для заданных ансамблей сигналов S.

Задача 1. Построить и изобразить сигнальное созвездие S для следующих ансамблей сигналов . Для каждого из них функция и параметр  – заданное целое число.

1)	2)
3)	4)
5)

При решении каждой из задач разумно придерживаться следующего плана:

а) найти ортонормированный базис

б) найти координаты каждого из векторов ансамбля S;

в) найти точки s⁽ⁱ⁾ сигнального созвездия S и изобразить их в .

Решение задачи 1.1.

а) Для нахождения базиса заметим прежде всего, что , а , поэтому базис системы совпадает с базисом его подсистемы . Легко убедиться, что векторы и линейно независимы, если (при и некоторых и независящих от ), то . Пусть , тогда, поскольку то . Полагая последовательно при , получим и Если то при также получим . Поэтому пара функций образует базис ансамбля . Поскольку скалярное произведение в функциональном пространстве задано с помощью равенства , то скалярное произведение

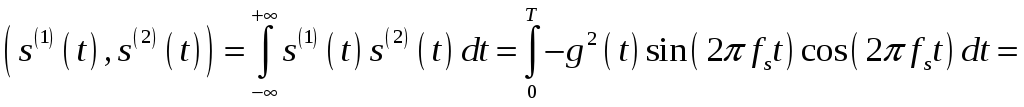
Отсюда следует, что базисные функции и ортогональны. Найдём квадраты длин векторов и .

Аналогично убедимся, что .

Поэтому в качестве ортонормированного базиса в линейной оболочке ансамбля можно взять где Поэтому

б) Из последовательных равенств следует, что

Поэтому в базисе функции и имеют, соответственно, координаты: и .

При изоморфизме евклидовых пространств и : , , где , . Тогда при этом отображении ансамбль перейдёт в созвездие S. Именно, Здесь

в) Изобразим полученное созвездие на координатной плоскости (см. рис. 2).

Решение 1.2. идентично решению задачи 1.1. Однако возможен другой подход, использующий известные формулы тригонометрии. Для сокращения записей введем обозначение: и выразим заданные здесь функции через функции задачи 1.1.

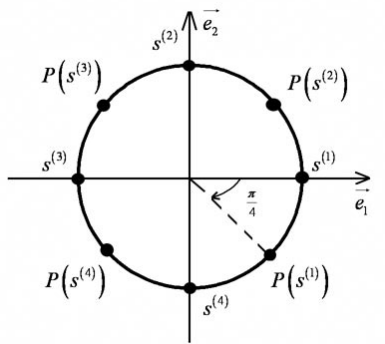
Рис. 2

Аналогично,

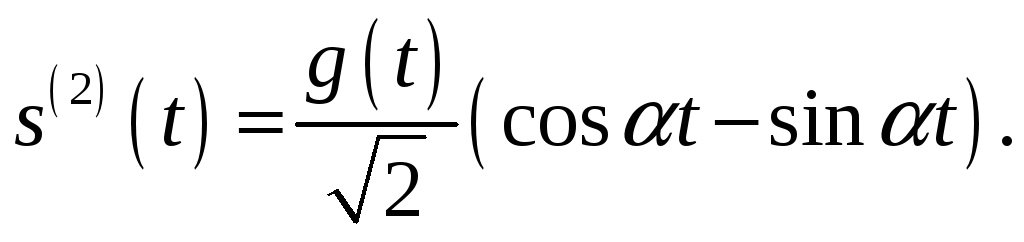
Таким образом, 1-й вектор задачи 1.2. есть нормированная сумма 1-го и 4-го векторов задачи 1.1, а 2-й вектор – нормированная сумма первых двух векторов задачи 1.1.

По линейности: нормированная сумма 2-го и 3-го векторов из задачи 1.1 есть 3-й вектор, данной задачи и нормированная сумма 3-го и 4-го векторов из задачи 1.1 есть 4-ый вектор данной задачи.

Поэтому созвездие S задачи 1.2 получается из соответствующего созвездия задачи 1.1 с помощью поворота Р по часовой стрелке на угол (см. рис. 2).

Решения задач 1.3 – 1.5 предлагаем провести самостоятельно. При решении целесообразно сравнивать заданные ансамбли сигналов с ансамблями сигналов предыдущих двух задач.

Замечание 1. Из решения задач следует, что линейные оболочки ансамблей сигналов задач 1.1 и 1.2 совпадают и содержат ансамбли сигналов задач 1.3 – 1.5. Поэтому сигнальные созвездия, построенные во всех задачах, могут быть изображены на одном рисунке, на котором изображается сигнальное созвездие S, соответствующее изоморфизму , определенному в задаче 1.1.

Замечание 2. Число М сигналов в ансамбле называется размером ансамбля, а размерность  – размерностью ансамбля.

Прежде чем сформулировать следующую задачу, сделаем некоторые пояснения по поводу задания двумерных ансамблей и их созвездий. Ввиду двумерности ансамбля, его элементы разумно описывать двумя целочисленными параметрами. Такое описание можно задать формулой

, (*)

где

Здесь Коэффициенты , где индекс

Базис параметр .

Задача 2. Построить ансамбль сигналов, заданных формулой (*), при Найти сигнальное созвездие S этого ансамбля и изобразить его на координатной плоскости.

Решение. Так как , то ; , и так как то . Поэтому множество , определенное выше, имеет вид

Биекция между порядковыми номерами сигнала и парой чисел устанавливается формулой

При и следовательно, имеем сигналы где .

При и следовательно, имеем сигналы где .

При и следовательно, имеем сигналы где .

При и, следовательно, имеем сигналы где .

Таким образом, ансамблю сигналов можно сопоставить матрицу двойных индексов:

Сквозная нумерация сигналов осуществляется по строкам матрицы I. Так, например, элементу (1,2) матрицы I соответствует сигнал а элементу (3,3) матрицы I соответствует сигнал

При изоморфизме построенном с помощью базиса , указанного выше, каждому сигналу соответствует вектор вида

Так, например, сигналу соответствует вектор а сигналу соответствует вектор Поскольку и принимают значения из множества то, согласно установленному выше соответствию, можно выписать координаты всех векторов

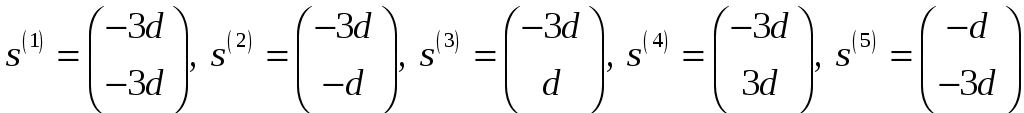и т.д. 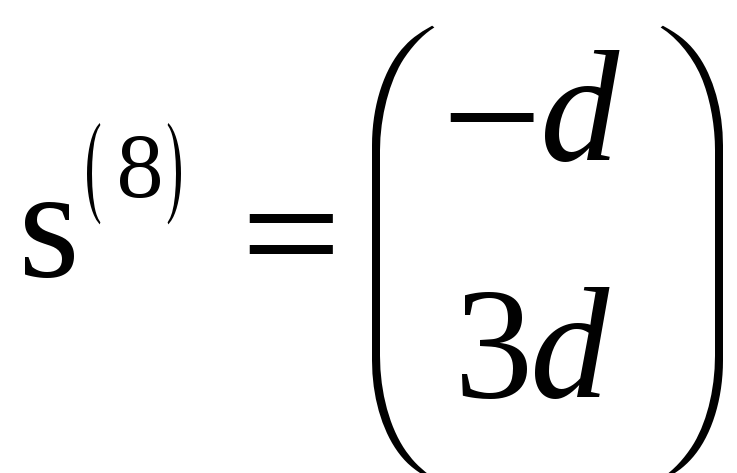и т.д. .

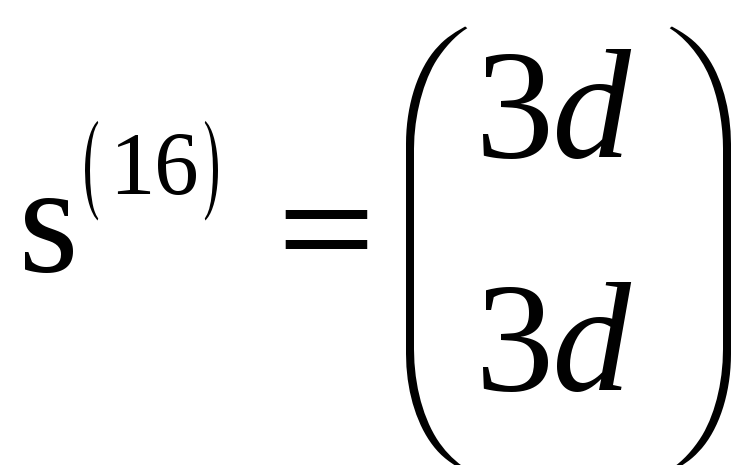Соответственно координатам векторов полученного сигнального созвездия, расположение его точек на координатной плоскости показано на рис. 3.

Задача 3. Доказать, что ансамбль сигналов , заданный формулой (*) при М = 4 совпадает с ансамблем сигналов задачи 1.2.

Указание. Для решения необходимо построить матрицу двойных индексов I и установить биекцию между элементами этой матрицы и порядковыми номерами сигналов заданного ансамбля. Построенное созвездие должно совпадать с созвездием задачи 1.2.

Рис. 3

Задача 4. Построить сигнальное созвездие для ансамбля сигналов, заданных формулами:

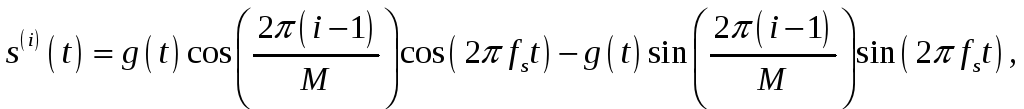
где

Решение. Легко проверить, что векторы 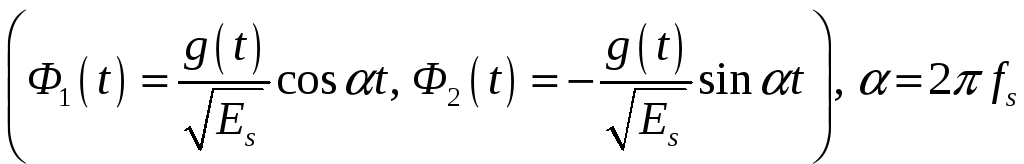образуют ортонормированный базис линейной оболочки . Очевидно, и в базисе его координаты . Вектор имеет координаты в том же базисе, а координаты вектора в базисе , суть

Нетрудно проверить далее, что скалярный квадрат Отсюда следует, что все векторы принадлежат окружности с центром в начале координат радиуса . Более того, они лежат в вершинах правильного М-угольника, одной из вершин которого является точка с координатами В самом деле, если  – угол между векторами и , и , то 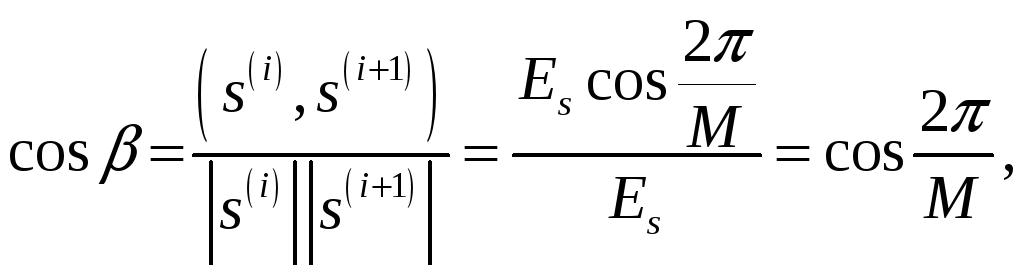откуда следует, что . Таким образом, не зависит от i, откуда и следует наше утверждение, касающееся структуры созвездия S. На рис. 4 изображено созвездие S, отвечающее числу М = 8.

Рис. 4