Загальні вказівки

Розв’язування задач з механіки потребує від студента вміння правильно вибрати систему відліку, виконати рисунок у вибраній системі координат та застосувати закони і формули фізики для фізичних величин, які потрібно знайти у даній задачі. Приблизний алгоритм розв’язання задач з механіки такий:

1. записати коротку умову задачіта та перевести всі величини в систему СІ;

2. вибрати тіло відліку, відносно якого буде розглядатись рух тіл у даній задачі;

3. вибрати систему координат (Ох або Ох-Оy) і виконати рисунок, на якому зобразити:

• вектори швидкостей і прискорень усіх тіл, що входять до умови задачі,

• вектори сил, що діють на ці тіла, і проекції векторів на координатні осі;

4. у задачі з кінематики записати кінематичні рівняння руху вздовж координатних осей;

5. у задачі з динаміки записати другий і третій закони Ньютона cпочатку у векторному вигляді, а потім у проекціях на координатні осі або використати основне рівняння динаміки обертального руху ;

6. використати закони збереження, якщо система тіл є замкненою;

7. використовуючи зв’язки між фізичними величинами задачі, які виходять з умови і геометрії задачі, написати додаткові рівняння таким чином, щоб число рівнянь дорівнювало числу невідомих величин;

8. розв’язати отриману систему рівнянь, записавши відповідь у загальному вигляді (тобто у вигляді формули);

9. підставити числові значення величин, що входять до відповіді, виконати обчислення й отримати числове значення відповіді; виділити відповідь у загальному вигляді (взяти в рамку, підкреслити) і числове її значення;

10. проаналізувати відповідь, оцінити її реальність, за необхідності перевірити розмірність отриманого результату.

Приклади розв’язування типових задач

Кінематика і динаміка поступального руху

№ 1. З вежі в горизонтальному напрямку кинули тіло з початковою швидкістю V_о = 10 м/с. Нехтуючи опором повітря, визначте для моменту часу t = 2 с після початку руху: 1) швидкість тіла; 2) радіус кривизни його траєкторії.

Дано:

V_о = 10 м/с

g = 9,8 м/с

t = 2 c

V, R – ?

Тіло бере участь у двох взаємно перпендикулярних рухах: рівномірному прямолінійному русі вздовж осі 0х (зі швидкістю V_х = V₀ = 10 м/с) та вільному падінні вздовж осі 0у (зі швидкістю V_у = gt) (рис. 1). Отже, швидкість тіла в точці А: .

Тіло рухається з прискоренням вільного падіння , яке може бути представлене сумою нормального і тангенціального прискорення: .

З рисунку видно, що нормальне прискорення тіла

.

З іншого боку, . Звідки: .

Обчислюючи, одержуємо:

 22 (м/с),  110 (м).

№ 2. Тіло обертається навколо нерухомої осі за законом:   = А+Вt+Сt², де A = 10 рад, В = 20 рад/c, С = –2 рад/c². Знайти повне прискорення точки, яка знаходиться на відстані r = 10 cм від осі обертання, у момент часу t = 4 c.

A = 10 рад

В =20 рад/c

С = –2 рад/c²

r = 10 cм = 0,1 м

t = 4 c

а – ?

Повне прискорення a точки, що рухається по кривій лінії, є векторною сумою тангенціального прискорення , напрямленого по дотичній до траєкторії, і нормального прискорення , напрямленого до центра кривизни траєкторії (рис. 2): . Оскільки вектори і взаємно перпендикулярні, то величина прискорення: . (1)

Модулі тангенціального і нормального прискорення точки обертового тіла виражаються за формулами

a_τ = εr, a_n = ω²r,

де ω – кутова швидкістьі тіла;

 – кутове прискорення.

Підставляючи ці вирази для а_τ і а_n до формули (1), знаходимо

. (2)

Кутову швидкість знайдемо, взявши першу похідну кута повороту  за часом:

ω = dφ/dt = B + 2Ct.

На момент часу t = 4 c модуль кутової швидкості

ω = (20 + 2∙(–2)∙4) рад/с = 4 рад/с.

Кутове прискорення знайдемо, взявши першу похідну від кутової швидкості за часом:

 = dω/dt = 2C = –4 рад/с².

Підставляючи значення ω, , r до формули (2), одержимо

а = 0,1  0,57 (м/с²).

№ 3. Вантаж масою 10 кг рухається по горизонтальній площині під дією сили 50 Н, яка прикладена під кутом =30 до горизонту. Коефіцієнт тертя 0,1. Визначити шлях, що пройде вантаж за 5 с після початку руху, і його швидкість.

Дано:

m = 10 кг

F = 50 H

 = 0,1

 = 30

g  10 м/с²

t = 5 c

V_o =0 Показуємо на рисунку всі сили, що діють на тіло: силу тяжіння, N -? силу нормальної реакції опори і силу тертя, і виберемо дві коор-динатні осі: вісь Ох спрямовуємо вздовж напряму руху тіла, вісь Оy – перпендикулярно до неї (рис. 3). Згідно з другим законом Ньютона:

.

Проектуємо це векторне рівняння на осі Ох і Оy і записуємо кінематичне рівняння руху в проекції на вісь Ох (шлях, який пройшло тіло за час t у рівноприскореному русі без початкової швидкості). Звідси, ураховуючи зв’язок сили тертя із силою реакції опори, маємо систему рівнянь:

ураховуючи, що F_x=FCos, F_y=FSin, та розв’язавши систему, знаходимо:

N = mg - FSin (з другого і третього рівняння),

F_тр= (mg - FSin) (з четвертого рівняння),

(з першого рівняння) і отримуємо відповіді:

, .

Підставляємо числові значення величин і знаходимо шлях, який пройшло тіло:

 44,8 (м).

 17,9 (м/с).

№4. За який час тіло зісковзне з похилої площини завдовжки 10 м, кут нахилу якої до горизонту =30, а коефіцієнт тертя 0,2? Знайти швидкість тіла внизу похилої площини.

Дано:

l = 10 м

 = 30

 = 0,2

g  10 м/с²

t - ? V - ?

На тіло діють: сила тяжіння, сила нормальної реакції опори і сила тертя (рис. 4). Покажемо на рисунку всі ці сили і виберемо дві координатні осі: вісь Ох спрямовуємо вздовж похилої площини, вісь Оy – перпендикулярно до неї. Вектори прискорення і швидкості направлені вниз уздовж похилої площини. Спроектуємо силу тяжіння на координатні осі: .

Запишемо другий закон Ньютона спочатку у векторному вигляді:

,

а потім таким самим чином, як і в попередній задачі, проектуємо це векторне рівняння на осі Ох і Оy, записуємо кінематичні рівняння руху в проекції на вісь Ох (шлях, який пройшло тіло за час t в рівноприскореному русі, та його швидкість), ураховуємо зв’язок сили тертя із силою реакції опори і маємо таку

систему рівнянь:

Звідси, з другого і третього рівняння, знаходимо:

N = mgCos,

F_тр =  m g Cos.

Підставляємо до першого рівняння і знаходимо:

,

.

Тепер з останнього рівняння системи виходить: . Підставляючи знайдене прискорення, записуємо у загальному вигляді: .

З останнього рівняння системи знаходимо швидкість, з якою рухається тіло внизу похилої площини: =.

Підставляємо числові значення величин і робимо обчислення:

2,5 (с).

2,6 (м/с).

№5. Автомобіль рухається по мосту зі швидкістю 72 км/год. Маса автомобіля 1000 кг. Знайти нормальне прискорення і силу тиску автомобіля на міст на його середині, якщо міст опуклий з радіусом кривизни 100 м.

Дано:

m = 1000 кг

V = 72 км/год =20 м/с²

R = 100 м

g = 9,8 м/с²

а_п, P -?

Показуємо на рисунку сили, що діють на автомобіль по вертикалі: силу тяжіння і силу нормальної реакції опо-

ри. Вісь Оy спрямовуємо вздовж радіуса вертикально вгору. Силу тиску на міст можна визначити з третього закону Ньютона: , а силу нормальної реакції опори – з другого закону Ньютона: . Урахуємо також кінематичний зв’язок прискорення зі швидкістю тіла при рівномірному русі тіла по колу): . Тепер запишемо ці рівняння у скалярному вигляді:

З останнього рівняння знаходимо нормальне прискорення: 4 (м/с²).

Підставляємо третє і четверте рівняння до другого і знаходимо силу реакції опори:

або .

Записуємо відповідь у загальному вигляді: .

Підставляємо числові значення величин і обчислюємо силу тиску автомобіля на міст: 5,810³ (Н).

№6. Визначити швидкість обертання супутника на орбіті, висота якої становить 630 км над поверхнею Землі, а також період його обертання навколо Земної кулі.

Дано:

R_з = 6370 км = 6,3710⁶ м

h = 630 км = 0,6310⁶ м

g_з = 9,8 м/с²

V-?

Згідно з другим законом Ньютона: ma_n = F_T (1),

де a_n = V²/R – доцентрове прискорення, F_T – сила тяжіння, яку знайдемо із закону всесвітнього тяжіння: . Тут G – гравітаційна стала, m – маса супутника, M – маса Землі, R = R_з+ h – радіус орбіти. Підставляючи у формулу (1), отримуємо: або (2).

Враховуючи, що , виразимо звідси масу Землі: і підставимо у формулу (2), звідки маємо: , або

Обчислюємо: 7,5410³ (м/с).

Період обертання визначимо з формули: .

Обчислюємо: 5,8310³ (c).

Закони збереження

№7. Снаряд, що летів горизонтально зі швидкістю 10 м/c, розірвався на два осколки масою 3 і 2 кг. Швидкість більшого осколка збільшилася до 25 м/с і він продовжував рухатися в тому самому напрямку. Визначити швидкість меншого осколка, напрямок його руху, а також його кінетичну енергію.

Дано:

V = 10 м/c

m₁ = 3 кг

m₂ = 2 кг

V₁ = 25 м/с

V₂ -? W₂ -? Снаряд і осколки є замкненою системою, оскільки час розриву дуже короткий і дією зовнішніх сил на цей час можна знехтувати. Тому можна застосувати закон збереження імпульсу у векторному вигляді:

.

Показуємо на рисунку вектори швидкості снаряда до розриву і осколків після розриву. Припустимо, що другий осколок після розриву рухався в тому самому напрямку, що й перший. Проектуємо вектори на горизонтальну вісь Ох і враховуємо, що маса снаряда дорівнює сумі мас осколків. Одержимо систему з двох рівнянь:

Звідси знаходимо: .

Підставивши числові значення величин і виконавши обчислення, знаходимо:

-12,5 (м). Знак “–“ перед значенням швидкості показує, що другий осколок після розриву снаряда рухається у напрямку, протилежному до того, що показаний на рисунку.

Кінетичну енергію осколка знайдемо за формулою: .

Звідси: 156,25 (Дж).

№8. Кулька масою 100 г, яка рухається зі швидкістю 5 м/с, зіштовхується з нерухомою кулькою масою 400 г. Вважаючи удар центральним і абсолютно непружним, знайти швидкість кульок після зіткнення, а також частину кінетичної енергії, яка пішла на їхнє нагрівання.

Дано:

m₁=0,1 кг

V₁=5 м/с

m₂=0,5 кг

V-? W/W₁-? Кульки є замкненою системою, оскільки час зіткнення дуже малий і дією зовнішніх сил на цей час можна знехтувати. Тому можна застосувати закон збереження імпульсу у векторному вигляді:

.

Показуємо на рисунку вектори швидкості кульок до зіткнення і після зіткнення. Проектуємо вектори на горизонтальну вісь Ох і враховуємо, що швидкість другої кульки до зіткнення дорівнювала нулю. Одержимо рівняння у скалярному вигляді:

m₁V₁+0 = (m₁+m₂)V.

Звідки: .

Енергію, яка пішла на нагрівання тіл, знайдемо як різницю між початковою кінетичною енергією першої кульки і кінетичною енергією кульок після зіткнення:

. Тепер знаходимо: .

Підставляючи числові значення, отримуємо:

1 (м/с). 0,8.

№9. У брусок масою 990 г, розташований на горизонтальній поверхні, влучає куля масою 10 г, яка летить зі швидкістю 200 м/с, і застряє в ньому. Визначити відстань, яку пройде брусок до повної зупинки, якщо коефіцієнт тертя 0,2.

Дано:

m₂ = 990 г = 0,99 кг

m₁ = 10 г = 0,01 кг

V₁ = 200 м/с

V = 0

 = 0,2 Для знаходження відстані, яку пройде брусок до повної

g  10 м/с² зупинки, використаємо теорему про зміну кінетичної енер-

S-? гії: W – W_о = А_ТР ,

де W_о= і W = 0 – відповідно, початкова і кінцева кінетичні енергії,

А_ТР = -F_TP S – робота сили тертя.

Оскільки в даному випадку F_TP=N=(m₁+m₂)g, маємо:

, звідки: .

Для визначення швидкості V_o застосуємо закон збереження імпульсу для непружної взаємодії кулі й бруска (в проекції на вісь ОХ): m₁V₁+0 = (m₁+m₂)V_o,

звідки . Тепер знаходимо: .

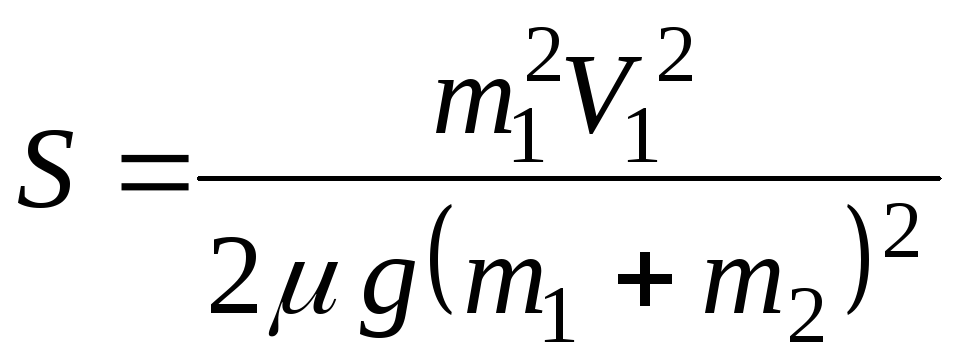Підставляємо дані з умови задачі й обчислюємо:

=1 (м/с).

№10. Знайти другу космічну швидкість для Місяця.

Дано:

g_м = 1,62 м/с²

R_м=1740 км = 1,7410⁶ м

V-?

Для знаходження другої космічної швидкості використаємо закон збереження

механічної енергії: W₁ = W₂ (1). Тут W₁ = W_1n+W_1к = – повна енергія тіла на поверхні Місяця, W₂ = W_2n+W_2к = 0 – повна енергія тіла на нескінченній відстані від поверхні Місяця. Урахуємо, що згідно із законом всесвітнього тяжіння , звідки маса Місяця: . Підставляючи у формулу (1), отримуємо: або , звідки: .

Обчислюємо: 2,3710³(м/с).

№11. Пружина розтягнута силою 2000 Н на 2 см. Визначити, яку роботу треба виконати, щоб розтягнути пружину ще на 1 см.

Дано:

F₁ = 2000 Н

l₁ = 2 см = 0,02 м

l = 1 см = 0,01 м

А – ?

За рахунок роботи зовнішньої сили змінюється потенціальна енергія пружини, тобто: А = W = W₂ – W₁ або W =. Жорсткість пружини визначимо із закону Гука: F₁ = kl₁, звідки . Підставляючи у першу формулу, знаходимо: .

Обчислюємо: 25 (Дж).

Динаміка обертального руху твердого тіла

№12. Через блок, який має форму диска радіусом R = 20 см і масою m = 200 г, перекинута мотузка. До кінців мотузки підвішені вантажі масою m₁=400 г і m₂ = 500 г. Знайти прискорення, з яким будуть рухатись вантажі, і кутову швидкість обертання блоку через 2 с після початку руху. Тертя не враховувати.

Дано:

m = 200 г = 0,2 кг Показуємо на рисунку вектори

m₁ = 400 г = 0,4 кг сил, які діють на тіла. Запишемо

m₂ = 500 г = 0,5 кг другий закон Ньютона для пер-

R = 20 см = 0,2 м шого і другого тіл в скалярному g  10 м/с² вигляді:

 -? m₁a = N₁ – F_T1 (1)

m₂a = F_T2 - N₂ (2)

Згідно з основним законом динаміки обертального руху: J = M (3)

де М = (N₂ -N₁)R – обертальний момент сил, які діють на диск,

J = mR²/2 – момент інерції диска,

 = a/R – кутове прискорення диска.

Ураховуючи, що згідно з третім законом Ньютона N₁ = N₁, N₂ = N₂ ,

маємо з рівняння (3): або (3).

Додаючи це рівняння і рівняння (1) і (2), маємо:

.

Звідки: =1 м/с².

Кутову швидкість обертання блока знайдемо з формули:

 = t =  12/0,2 = 10 (об/с).

№13. Платформа у вигляді диска масою 100 кг, у центрі якої знаходиться людина масою 60 кг, обертається з частотою 6 об/хв. З якою частотою буде обертатися платформа, коли людина перейде на її край.

Дано:

m₁ = 100 кг

m₂ = 60 кг

₁ = 6 об/хв = 0,1 об/с

₂ -?

Оскільки людина і платформа є замкненою системою, згідно із законом збереження моменту імпульсу:

(J₁+J₂)₁ = (J₁+J₂)₂,

де J₁ = m₁R²/2 – момент інерції платформи, J₂ = 0 – момент інерції людини, яка стоїть у центрі платформи, і J₂ = m₂R² – момент інерції людини на краю платформи, ₁=2₁ – початкова кутова швидкість і ₂ = 2₂ – кінцева кутова швидкість платформи з людиною. Звідси маємо:

Обчислюючи, отримуємо: 0,045 (об/с).

№14. З якою швидкістю скотиться куля з похилої площини заввишки 1 м? Куля котиться без проковзування.

Дано:

h =1 м

g = 9,8 м/c²

V_c -?

Для розв’язання задачі використаємо закон збереження механічної енергії: W₁ = W₂. Тут W₁ = mgh – потенційна енергія кулі нагорі, W₂ – кінетична енергія кулі внизу похилої площини. Кінетична енергія має дві складові – кінетичні енергії поступального руху і обертального руху:

W₂ = W_пост + W_об = .

Тут J_c = – момент інерції кулі відносно центральної осі. У випадку кочення без проковзування V_пост = V_об, де V_пост = V_с – швидкість поступального руху, V_об = R – швидкість обертального руху кулі. Звідси і повна кінетична енергія .

Підставляючи до початкової формули, отримуємо: mgh = , звідки

. Обчислюючи, знаходимо: 3,7 (м/с).

Механіка рідин і газів

№15. Вода тече у горизонтально розташованій трубі змінного перерізу. Швидкість води у широкій частині труби дорівнює 30 см/с. Визначити швидкість води у вузькій частині, діаметр якої у 2 рази менший, ніж діаметр широкої частини.

Дано:

₁ = 30 см/с = 0,3 м/с

d₁/d₂ = 2

₂ – ?

Виходячи з рівняння нерозривності та враховуючи, що і _, маємо .

Звідси: _.

Підставляючи числові значення, отримуємо: 1,2 (м/с).

Елементи спеціальної теорії відносності

№16. З якою швидкістю рухається протон у прискорювачі, якщо його збільшення маси дорівнює 5%?

Дано: Залежність маси тіла від швидкості визначається за m/m₀ = 0,05 формулою: . c = 310⁸ м/с Звідси: . Після перетворень  –? отримуємо: .

Обчислюючи, знаходимо:  0,22с  0,6510⁸ м/с .