31

Министерство образования Республики Беларусь

Учреждение образования

«МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ПРОДОВОЛЬСТВИЯ»

Кафедра прикладной механики

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

Задания для расчетно-графических и контрольных работ студентам специальностей 1-36 09 01 «Машины и аппараты пищевых производств» и 1-36 20 01 «Низкотемпературная техника» специализации 1-36 20 01 01 «Холодильные машины и установки»

дневного и заочного обучения по динамике

Могилев 2007

УДК 531(076)

Рассмотрены и рекомендованы к изданию кафедрой ПМ Протокол № 8 от 16 декабря 200 6 г.

Составитель к.т.н., доцент А.Я.Протас

Рецензент к.т.н., доцент В.П.Пахадня

Протас А.Я. Теоретическая механика. З а д а н и я для расчетно-графических и контрольных работ студентам специальностей 1-36 09 01 «Машины и аппараты пищевых производств» и 1-36 20 01 «Низкотемпературная техника» специализации 1-36 20 01 01 «Холодильные машины и установки» дневного и заочного обучения по динамике. – Могилев: УО МГУП, 2007. - 32с.

Настоящее пособие включает задания для контрольных работ № 3 и № 4 студентам-заочникам МАПП и ХМУ, часть из которых одновременно может использоваться для расчетно- графической работы по динамике студентами дневного обучения. Приведены условия, исходные схемы, необходимые таблицы данных, а также таблица для выбора вариантов задач по заданному шифру. Особенность пособия – большое количество вариантов заданий и возможность использования через Интернет в электронном виде.

Таблиц 17, рис. 80, библ. 4 названия.

© Протас Анатолий Яковлевич, 2007

© УО «Могилевский государственный университет продовольствия», 2007

Методические указания

Согласно программе курса теоретической механики, утвержденной в 2005г., студенты- заочники специальностей 1-36 09 01 «Машины и аппараты пищевых производств» и 1-36 20 01 «Низкотемпературная техника» специализации «Холодильные машины и установки» выполняют 4 контрольные работы:

№ 1,2 – по статике и кинематике– задачи С1-С4, К1-К4 [1];

№ 3 – по динамике – задачи Д1, Д2, Д3, Д4;

№ 4 – по динамике – задачи Д5, Д6, Д7, Д8.

Аналогичные расчетно-графические задания, но в меньшем объеме, выполняют студенты дневного обучения, поэтому пособие может быть использовано и теми и другими вместо [2], [3], [4].

Каждая задача в качестве заданных имеет 10 схем и таблицу с 10 вариантами условий. Поэтому студенту-заочнику для выбора исходных данных по каждой задаче нужно знать две цифры. По первой он выбирает схему, по второй - номер условия . Откуда взять эти две цифры? Во время сессии преподаватель, ведущий занятия со студентами-заочниками, присваивает каждому из них трехзначный шифр, согласно которому из специальной таблицы Д9 студенты выбирают отдельные двухзначные варианты к каждой задаче всех четырех контрольных работ. Ни шифр, ни варианты задач никакого отношения к номеру зачетной книжки не имеют, а относятся только к теоретической механике.

Всего предусмотрено 100 двухзначных вариантов задач, но, по усмотрению преподавателя, они могут быть преобразованы в трехзначные. Для этого к каждой задаче приведены дополнительные данные, представленные в таблицах Д1.2, Д2.2 и т.д. Количество вариантов в этом случае возрастает до 1000. Схема преобразования двухзначного варианта в трехзначный выбирается преподавателем.

Оформление контрольных работ осуществляется по общепринятым правилам, при этом в самом начале должен быть указан выданный трехзначный шифр по дисциплине, а также варианты каждой задачи. В обязательном порядке должны быть приведены исходные схема и данные. Излишние пояснения к решению не требуются, в то же время приводимых данных должно быть достаточно для свободной проверки работы. Рисунки должны быть четкими, с соблюдением правил черчения, а записи - ясными и не допускающими двойного толкования. Приведение одних ответов без расчетов неприемлемо, т.к. практически исключает возможность проверки выполненного решения.

Задача Д1

Динамика материальной точки

Зерно подается в хранилище по закрытому лотку АВД(АВ), представленному на рис. Д1.0-Д1.9 и имеющему один прямолинейный участок и второй – закругленный по радиусу R=0,8м. После схода с лотка оно продолжает движение в воздухе и, преодолев по вертикали и горизонтали расстояния b и a, попадает в точку К, т.е. касается стенки со скоростью V_к. Прямолинейный участок лотка наклонен к горизонту под углом α, а криволинейный соответствует центральноу углу β=90⁰ (для двухзначных вариантов). Имея в начальный момент в точке А скорость V₀, зерно преодолевает оба участка и в точке Д отрывается от него, при этом на преодоление прямолинейного участка длиной l затрачивается время t=1с, а на свободное движение в воздухе - t₁. Коэффициент трения скольжения на прямолинейном участке f=0,1, силами сопротивления трения скольжения на криволинейном участке пренебречь, а для участка свободного падения считать, что сопротивление воздуха отсутствует. Определить величины, указанные в таблице Д1.1 по вариантам.

Таблица Д1.1

Вариант	*0		*1	*2	*3	*4	*5	*6	*7	*8	*9
Задано
V0, м/с	6	8		10	4	5	4	9	6	8	5
α, град	60		30	40	70	50	70	40	60	30	50
a, м			3	4		2		3	2
b, м	2				3		4			3	2
Найти
l	+					+	+		+
b			+	+		+		+	+
a	+				+		+			+	+
Vк			+		+					+
t1				+				+			+

В таблице Д1.2 приведены дополнительные данные по углу β и времени t, с помощью которых варианты задач по усмотрению преподавателя могут быть превращены в трехзначные.

Таблица Д1.2- Дополнительные данные для расчетов при трехзначных вариантах

Вариант	**0		**1	**2	**3	**4	**5	**6	**7	**8	**9
β, град	90	30		90	30	20	90	30	20	90	90
t, с	1,0		0,8	0,4	1,2	0,6	1,0	0,8	0,4	1.2	0,6

Задача Д2

Исследование относительного движения материальной точки

Капсула М массой 40г, имея начальную скорость V₀=2м/с, движется в пазу блока прямоугольной формы массой 4кг, который, в свою очередь, перемещается по плоскости или вертикально с постоянным ускорением а=3м/с² (для двухзначных вариантов), направленным в сторону, указанную на рис. Д2.0-Д2.9. Наклон плоскости к горизонту и наклон паза к основанию блока определяются углами α и β. При этом угол α задан в таблице Д2.1 по вариантам, а угол β=30⁰. Отсутствие угла β на схеме означает, что его величина равна нулю. Движение блока происходит под действием сил, не рассматриваемых в этой задаче, а на движении капсулы внутри паза сказываются не только силы тяжести и силы инерции, но и силы трения скольжения, определяемые коэффициентом f, который задан в таблице Д2.1 по вариантам. Размер капсулы несколько меньше размера паза, поэтому под действием сил она может быть прижата или к одной, или к другой стенке паза. В начальный момент движения капсула находится посредине паза АВ и ее скорость V₀ направлена от А к В. Для трехзначных вариантов ее направление оговаривается особо. Считая, что движение блока и капсулы началось одновременно, определить закон относительного движения капсулы в пазу и ее положение относительно середины паза в момент времени t=0,8с.

Таблица Д2.1

Вариант	*0	*1	*2	*3	*4	*5	*6	*7	*8	*9
α,град	20	0	10	20	20	10	0	20	10	10
f	0,1	0,2	0,05	0,15	0,05	0,2	0,1	0,2	0,15	0,1

В таблице Д2.2 приведены дополнительные данные по ускорению а и направлению начальной скорости V₀, с помощью которых варианты задач по усмотрению преподавателя могут быть превращены в трехзначные.

Таблица Д2.2 - Дополнительные данные для расчетов при трехзначных вариантах

Вариант	**0	**1	**2	**3	**4
а,м/с2	3	2,5	1	2	1,5
Направление V0	АВ	АВ	ВА	АВ	ВА
Вариант	**5	**6	**7	**8	**9
а,м/с2	1,5	2	1	2,5	3
Направление V0	АВ	ВА	АВ	ВА	ВА

Задача Д3

Исследование поступательного и вращательного движений твердого тела

Груз массой m₁ буксируется по наклонной плоскости с помощью каната, наматываемого на барабан редуктора, который представляет собой два шестеренчатых блока, находящихся в зацеплении или соединенных тросом, как показано на рис. Д3.0 – Д3.9. Радиусы блоков R₂=24, r₂=18, R₃=22, r₃=8см, а радиусы инерции ρ₂=20, ρ₃=16см. Масса блоков составляет: m₂=32, m₃=36кг. Движущий момент М от электродвигателя передается на блок 3, а к блоку 2 приложен постоянный или зависящий от угловой скорости блока 2 момент сопротивления М_с. Угол наклона плоскости к горизонту α для двухзначных вариантов составляет 30⁰ (на рисунках показан положительный), а коффициент трения скольжения по ней груза f=0,1. Движущий момент М, момент сопротивления М_с и масса груза 1 заданы в таблице Д3.1 по вариантам. В начальный момент скорость буксируемого груза составляла 0,2м/с.

Определить закон изменения угла поворота ведущего блока 3 как функцию времени, а для момента времени t=1с также усилия, действующие в зацеплении блоков (или соединительном тросе) и в канате, с помощью которого осуществляется буксировка груза 1.

Таблица Д3.1

Вариант	*0	*1	*2	*3	*4
М, Н·м	700	650+30t	670	720	570+20t
Мс, Н·м	30ω2	25	50ω2	20ω2	40
m1	160	220	100	150	140
Вариант	*5	*6	*7	*8	*9
М, Н·м	680+50t	750	600+40t	690	610+60t
Мс, Н·м	30	60ω2	20	40ω2	35
m1, кг	190	170	120	200	180

В таблице Д3.2 приведены дополнительные данные по углу наклона плоскости α, коэффициенту трения f и моменту времени t, с помощью которых варианты задач по усмотрению преподавателя могут быть превращены в трехзначные.

Таблица Д3.2 - Дополнительные данные для расчетов при трехзначных вариантах

Вариант	**0	**1	**2	**3	**4
α,град	30	0	-20	60	0
f	0,1	0,05	0,1	0,05	0,1
t,с	1	1,5	3	2	2,5

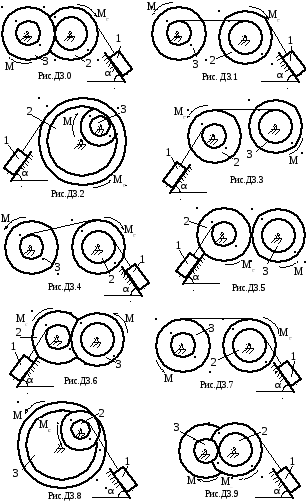
Таблица Д3.2(Продолжение)

Вариант	**5	**6	**7	**8	**9
α,град	90	30	-15	90	60
f	0	0,05	0,05	0	0,1
t, с	3	2,5	1	1.5	2

Задача Д4

Применение теоремы об изменении кинетической энергии к изучению движения механической системы

Механическая система состоит из нескольких тел, соединенных между собой с помощью тросов, как показано на рис. Д4.0 – Д4.9. Под действием сил тяжести она приходит в движение из положения покоя, при этом преодолеваются силы трения скольжения и качения по наклонной плоскости, определяемые коэффициентами f и δ. Кроме этого, движению препятствует момент сопротивления М_с на ступенчатом блоке 2, обусловленный трением в подшипниках или действием спиральной пружины, связанной с этим блоком. Плоскости наклонены к горизонту под углами α и β, а масса тел составляет m₁=200, m₂=30, m₄=10, m₅=8кг. Радиусы колес и блоков соответственно равны R₂=20, r₂=10, R₃=15см. Радиус инерции ρ₂=16см, а масса тела 3 равномерно распределена по его ободу. Длину l стержня 4 принять равной 80см, а угол наклона плоскости β - 30 градусам. Масса тела m₃, момент сопротивления М_с, угол α и коэффициент трения качения δ заданы в таблице Д4.1 по вариантам.

Пренебрегая массой соединительных тросов и считая, что коэффициент трения скольжения f=0,1, определить величину и направление скорости тела 1 и угловой скорости блока 2 в момент времени, когда он повернется на угол φ₂=1,5π. Считать, что момент сопротивления М_с направлен против движения независимо от того, в какую сторону будет перемещаться система, а качение катков (блоков) 3 происходит без проскальзывания.

Таблица Д4.1

Вариант	*0	*1	*2	*3	*4
Мс,Н·м	5φ+5	6	2φ+4	5	4φ+6
m3,кг	250	120	280	140	210
α,град	30	45	60	90	30
δ,м	0,02	0,03	0,04	0,02	0,04

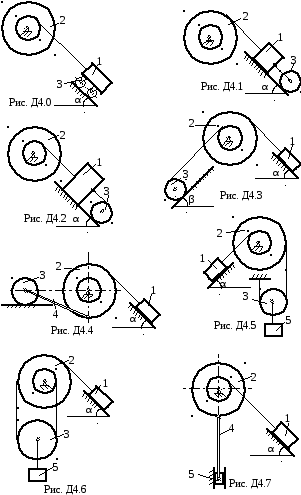
Таблица Д4.1(Продолжение)

Вариант	*5	*6	*7	*8	*9
Мс,Н·м	3φ+5	6	3φ+4	5	4
m3,кг	180	160	230	240	150
α,град	40	60	50	35	45
δ,м	0,03	0,02	0,03	0,03	0,04

В таблице Д4.2 приведены дополнительные данные по массе тела m₁, углу поворота ступенчатого блока φ₂ и коэффициенту трения скольжения груза 1 по плоскости f, с помощью которых варианты задач по усмотрению преподавателя могут быть превращены в трехзначные.

ТаблицаД4.2 - Дополнительные данные для расчетов при трехзначных вариантах

Вариант	**0	**1	**2	**3	**4
m1,кг	200	180	240	140	220
φ2,рад	1,5π	2π	π	3π	2,5π
F	0,1	0,15	0,05	0,2	0,1
Вариант	**5	**6	**7	**8	**9
m1,кг	170	150	210	160	230
φ2,рад	1,5π	3π	2π	2,5π	π
f	0,05	0,15	0,2	0,2	0,1