Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Южный Федеральный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Алгебра модуль2..doc

Скачиваний:

Добавлен:

05.11.2018

Размер:

854.53 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

2.6 Отыскание обратной матрицы методом Гаусса

Для отыскания обратной матрицы методом Гаусса достаточно в уравнение (2.8) положить . Если матрица обратима, тогда уравнение

имеет единственное решение

В этом случае матрица л‑эквивалентна матрице . Если же матрица необратима, тогда в силу предложения 1.6. л‑эквивалентная ей матрица будет иметь нулевую строку.

В результате, алгоритм выяснения обратимости матрицы и отыскания матрицы методом Гаусса принимает следующий вид.

Составляем матрицу и строчными элементарными преобразованиями приводим её к виду .

1) Если указанные преобразования осуществить удаётся, матрица обратима и .

2) Если указанные преобразования осуществить не удаётся (в процессе преобразований появляется нулевая строка), матрица необратима.

Пример 7. Выяснить, является ли матрица обратимой, и в случае её обратимости найти матрицу ,

◄ Применяя только что изложенный алгоритм, получаем

. ►

Упражнения

При решении систем линейных алгебраических уравнений, в особенности, на первых парах у решающих часто появляются вычислительные ошибки. В связи с этим полезно использовать вычислительную схему методы Гаусса с контрольным столбцом. Контрольный столбец является суммой всех столбцов расширенной матрицы СЛАУ и выписывается справа от неё. Элементарные преобразования метода Гаусса применяются к контрольному столбцу наравне с остальными столбцами. Контроль за правильностью вычислений состоит в том, что после каждого элементарного (строчного) преобразования измененный элемент контрольного столбца должен равняться сумме всех предыдущих элементов соответствующей строки. Если это условие нарушается ,следует искать вычислительную ошибку!

Пример 8. Решить методом Гаусса следующую систему уравнений.

◄ Выписываем расширенную матрицу системы с добавленным контрольным столбцом

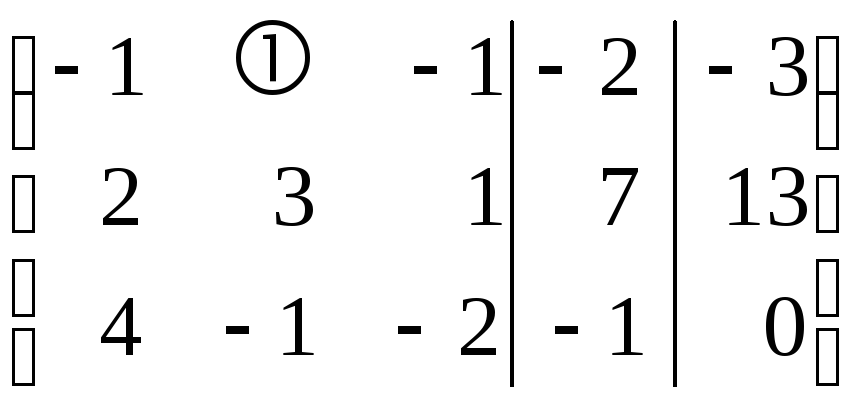В качестве ведущего выбираем второй элемент первой строки и проводим элементарные преобразования . Получаем матрицу

Проводим контроль вычислений второй и третьей строк:

Следовательно, при вычислении второй строки допущены ошибки. Действительно, в первом столбце второй строки после преобразования должно быть . Остальные вычисления правильны: . Проведем исправления, продолжаем вычислительный процесс:

Вновь проводя вычислительный контроль для первой и второй строк, получаем:

Вновь ошибка вычислений во второй строке, вместо 16 следует записать 18. Далее,

Проводя последний вычислительный контроль замечаем, что в первой строке допущена ошибка внимания, в четвертом столбце элемент не преобразован: . Наконец, матрица

является приведенной

Поскольку ошибки внимания преследуют неопытного вычислителя на каждом шагу, следует убедиться в правильности полученного результата. Для этого нужно сделать проверку, подставив полученные значения неизвестных в исходную систему и убедиться, что после этого её уравнения превращаются в числовые равенства. ►

Следующие системы уравнений решить методом Гаусса, указав общее и одно частное решения.

1. 2.

3. 4.

5. 6.

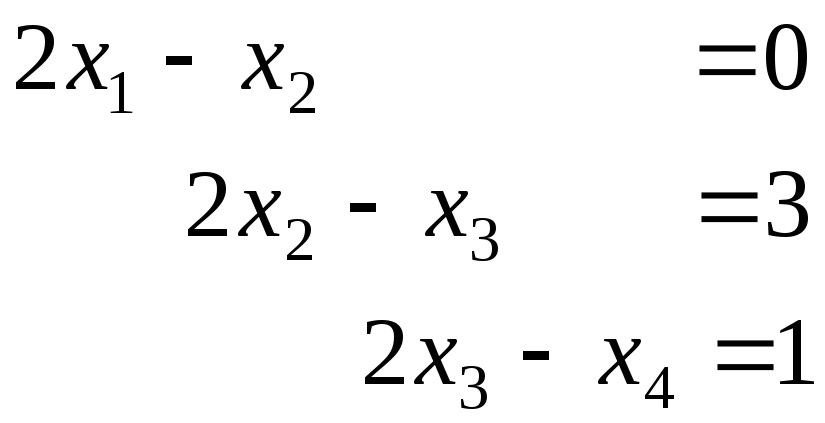
7. 8.

9. 10.

11.

Если коэффициенты системы уравнений зависят от параметров, то задача решения такой системы сводится к определению тех значений параметров, при которых система имеет решения и нахождению этих решений.

Если параметр входит в один коэффициент системы, целесообразно при использовании метода Гаусса проводить такие элементарные преобразования, которые не приводят к «расползанию» параметра по матрице.

Пример 9.

◄

На этом этапе мы замечаем, что при , т.е. при , система несовместна, а при система является определенной, так как проводя преобразование , мы получаем, что

и, следовательно, единственное решение системы имеет вид:

Например, при . Предлагаем читателю для вычислительного контроля проверить, что при вектор действительно удовлетворяет исходной системе уравнений.

Наличие параметра в СЛАУ не обязательно приводит к существованию таких его критических значений, как в примере 9, при которых СЛАУ меняет своё качество.

Пример 10.

◄

Таким образом, рассматриваемая СЛАУ при любых значениях является определенной, а её единственное решение имеет вид:

►

Пример 11.

Предлагаем читателю убедиться, что при любых значениях данная СЛАУ является несовместной.

Если параметр входит в несколько коэффициентов рассматриваемой системы уравнений, прежде чем применять метод Гаусса, часто целесообразно, провести вспомогательные преобразования, учитывающие структуру матрицы СЛАУ.

Пример 12.

◄ Проведем следующее вспомогательное преобразование:

Ясно, что при () система несовместна. Полагая , проводим преобразование , после этого следуем стандартному алгоритму метода Гаусса.

Из вида последней матрицы следует, что мы обнаружили еще одно критическое значение параметра .

Если , мы можем провести элементарное преобразование .

И тогда, применяя стандартный ход метода Гаусса, получаем, что:

то есть СЛАУ является определенной, а её единственное решение имеет вид

(2.12)

Если же , мы получаем СЛАУ

которая совместна и неопределенна, а её общее решение имеет вид:

, где . (2.13)

Таким образом, при исходная СЛАУ несовместна, при и она определена и имеет решение вида (2.12), а при и она совместная, неопределенная и имеет общее решение вида (2.13).►

Пример 13.

◄

Для того, чтобы эта система была совместна, необходимо, чтобы , т.е. . Тогда общее решение имеет вид:

или

.►

Пример 14. При каких значениях параметра система

имеет ненулевые решения?

◄

Пусть (случай исследуем отдельно). Сократим во втором уравнений на . Получим:

так как

Аналогично, если , то имеем систему с матрицей

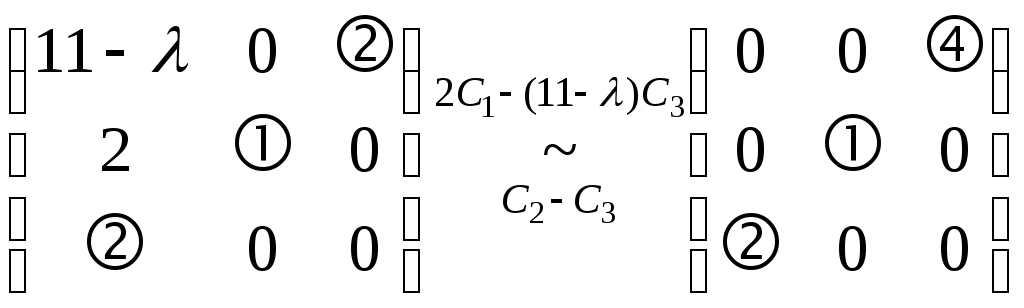Следовательно, если , система имеет лишь тривиальные решения. При имеем систему:

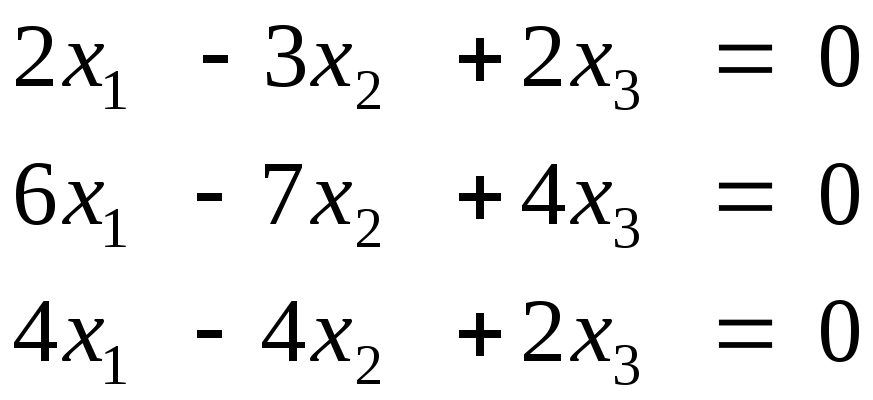Используя предыдущие выкладки, получаем:

Так как является свободной переменной, то общее решение СЛАУ в этом случае имеет вид

При имеем систему

Используя предыдущие выкладки, получаем

В этом случае общее решение СЛАУ имеет вид

.►

Исследовать систему уравнений в зависимости от параметра . Найти общее и одно частное решения.

12. 13.

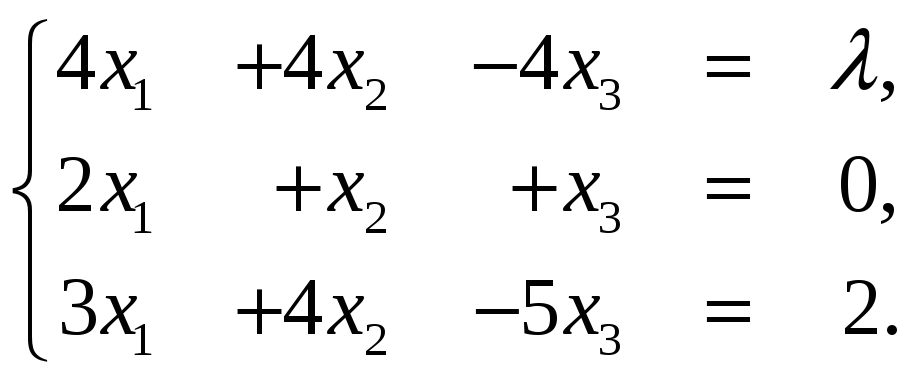
14. 15.

16.

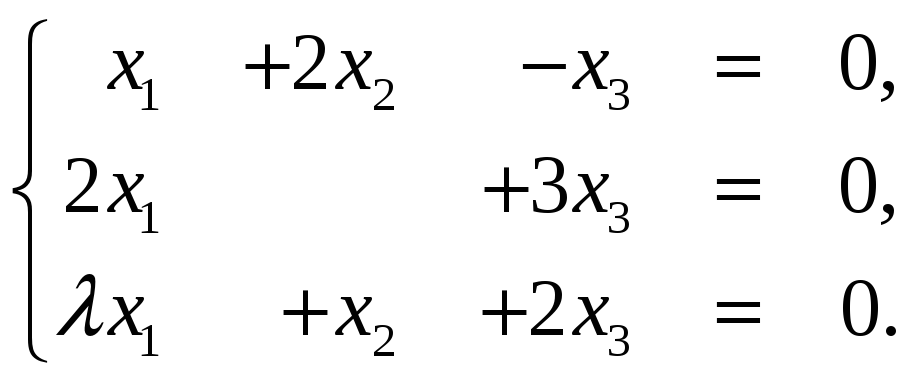
17. Найти матрицу , воспользовавшись методом Гаусса, если матрица имеет вид:

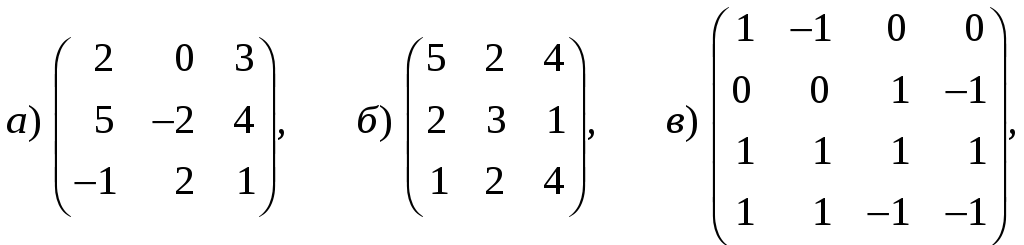При решении матричных уравнений вида (1.24)-(1.26) можно использовать модификации вычислительных схем, рассмотренных в примерах 5 и 6.

Пример 15. Решить матричное уравнение , где

, .

◄ Составим блочную матрицу и столбцовыми элементарными преобразованиями, совершаемыми над этой матрицей, приведем блок к виду . Тогда на месте блока появится решение нашего уравнения,

Проверим, что матрица является решением рассматриваемого уравнения,

. ►

Пример 16. Решить матричное уравнение , где

, , .

◄ Применим следующую вычислительную схему.

1) Вводим обозначение , тогда .

2)Составляем блочную матрицу и приводим блок к виду строчными элементарными преобразованиями как при решении уравнения ,

;

блоком после этого наращиваем блок сверху и приводим блок столбцовыми элементарными преобразованиями к виду как при решении уравнения ,

После этого на месте блока появится решение исходного уравнения.

Действительно,

Таким образом,

. ►

18. Решить матричные уравнения:

а) , б) ,

в) ,

г) д)

е) .

Метод Гаусса пригоден также для решения матричных уравнений с необратимыми, в частности, неквадратными матричными коэффициентами. Пример 17. Решить матричное уравнение , где