МИНИСТЕРСТВО ОБРАЗОВАНИЯ и НАУКИ РФ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное образовательное учреждение

высшего профессионального образования

«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Факультет математики, механики и компьютерных наук

Ростовский-на-Дону государственный университет

В.Б. Дыбин

Алгебра

Лекции и практика

Методическое пособие первокурснику

Часть 1

Модуль 2

Системы линейных алгебраических уравнений

2008 г.

Гл. 2. Системы линейных алгебраических уравнений

Матричное исчисление, построенное в лекциях I-V, позволяет провести первичное исследование систем линейных алгебраических уравнений (СЛАУ), опирающееся на метод, носящий имя великого немецкого математика Карла Гаусса (1777-1855).

Поскольку СЛАУ можно трактовать как матричное уравнение специального вида, обоснование метода Гаусса даётся на языке элементарных матриц и матричных уравнений. В свою очередь, метод Гаусса позволяет построить удобный алгоритм решения ряда матричных уравнений, в частности, алгоритм вычисления обратной матрицы.

Лекция VI.

План

2.1 Классификация СЛАУ

2.2 Метод Гаусса решения СЛАУ

2.1 Классификация слау

Системы линейных алгебраических уравнений составляют основной аппарат линейной алгебры, а их исследование основано на алгебре матриц.

Общий вид системы линейных уравнений с неизвестными даётся формулами

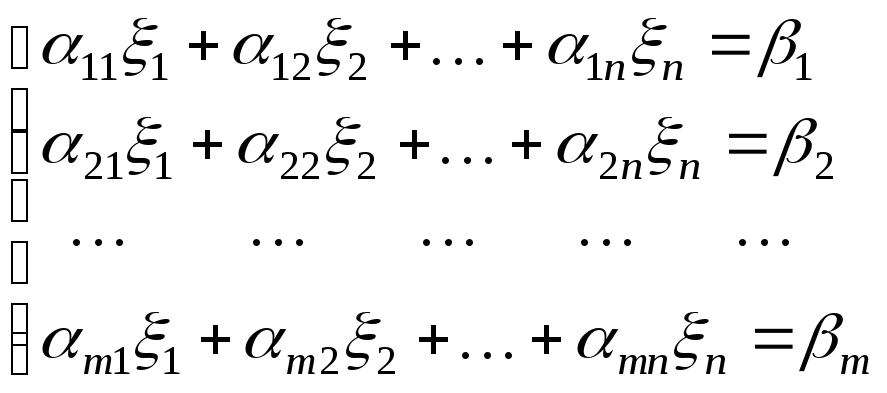(2.1)

В этих формулах называются неизвестными, – коэффициентами при неизвестных, – свободными членами (или правыми частями). Коэффициенты порождают матрицу

, (2.2)

которая называется матрицей (или основной матрицей) СЛАУ (2.1), . Неизвестные , порождают столбец неизвестных

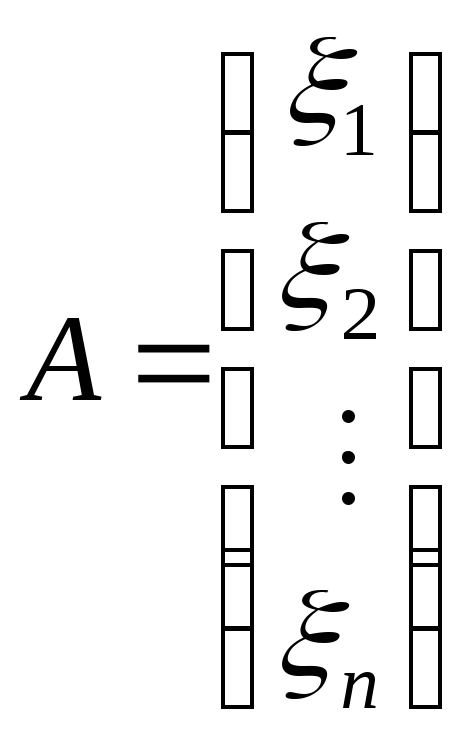, (2.3)

а правые части – столбец правых частей

. (2.4)

Матрица

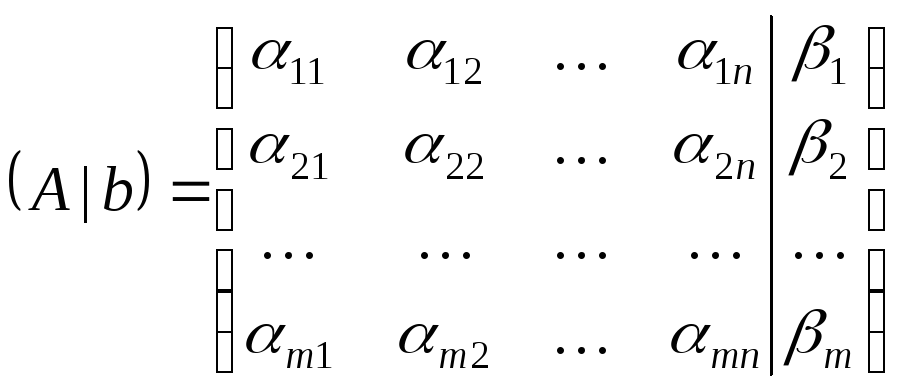(2.5)

называется расширенной матрицей СЛАУ (2.1).

Арифметический вектор

.

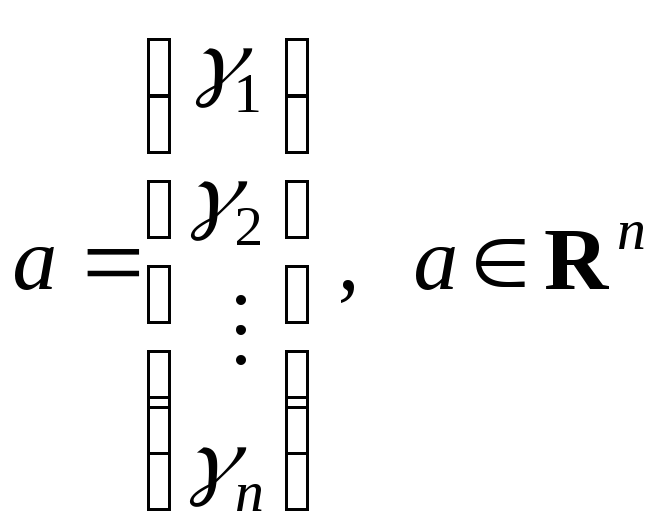называется решением СЛАУ (2.1), если при подстановке чисел в уравнения (2.1) соответственно вместо мы получаем систему верных числовых равенств.

СЛАУ называется совместной, если она имеет хотябы одно решение, и несовместной, если она не имеет ни одного решения. Если СЛАУ имеет только одно решение, она называется определённой, а если число решений больше 1 – неопределённой.

В результате мы получаем следующую классификацию СЛАУ. Пусть

– множество решений СЛАУ, а – мощность (число элементов) множества

. Тогда

Если все правые части СЛАУ равны нулю, , она называется однородной, в противном случае СЛАУ называется неоднородной. Однородная СЛАУ всегда совместна, т.к. имеет нулевое решение

.

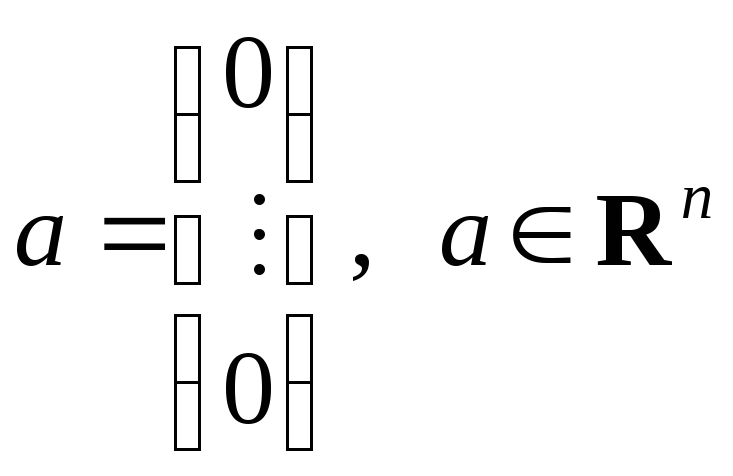Множество всех решений СЛАУ будем называть её общим решением, а одно фиксированное решение – частным решением. СЛАУ вида (2.1) иногда удобно представлять в виде матричного уравнения

. (2.6)

где – матрица вида (2.2), – вектор-столбец вида (2.3), а – вектор-столбец вида (2.4). Для того чтобы убедиться, что уравнения (2.6) и СЛАУ (2.1) равносильны (т.е. одновременно неразрешимы или разрешимы, причём в последнем случае их решения совпадают), достаточно в левой части равенства (2.6) провести умножение матрицы на вектор-столбец . Применив после этого принцип равенства матриц, получаем, что матричное равенство (2.6) эквивалентно системе равенств (2.1).

2.2 Метод Гаусса решения слау

Метод последовательного исключения неизвестных часто применяется при решении всевозможных систем уравнений, в частности, тех, которые встречаются в школьном курсе математики. Если выразить, например, из первого уравнения системы (2.1) и подставить это выражение в остальные уравнения, потом выразить из второго “нового” уравнения, подставив это выражение в остальные “новые” уравнения и т.д., то через конечное число шагов мы получим уравнение, содержащее только . Найдя решение этого уравнения, путём обратной подстановки его в предыдущие “новые” уравнения можно найти значения всех неизвестных . Такова идеальная схема которая молчаливо опирается на целый ряд допущений (например, на то, что , иначе для отыскания не хватит уравнений).

Метод Гаусса в современном изложении представляет собой, во-первых, такую модификацию метода исключения неизвестных, которая позволяет исследовать любые системы вида (2.1). А, во-вторых, алгоритм Гаусса, используя аппарат алгебры матриц, даёт такую формализацию метода исключений, которая позволяет существенно сократить объём выкладок, резко возрастающий вместе с ростом числа уравнений и числа неизвестных .

Прежде чем приступить к изложению метода Гаусса в общем случае, продемонстрируем его на простом примере.

Пример 1. Рассмотрим систему уравнений

.

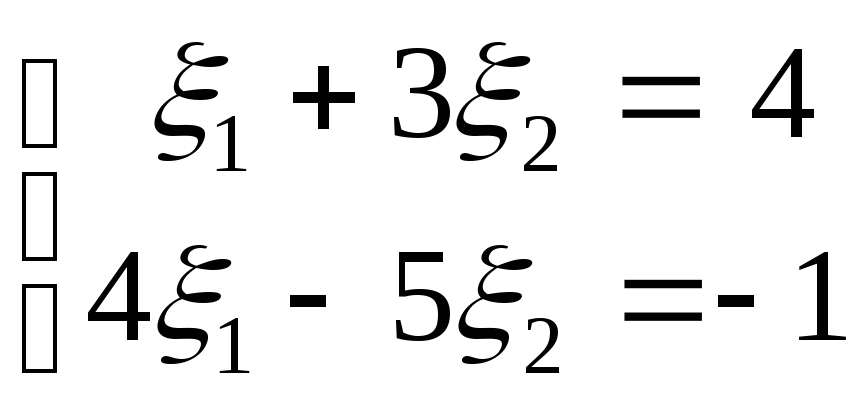Вычитая из второго уравнения 4 первых, получаем систему

.

Разделив обе части второго уравнения на (-17), приходим к системе

.

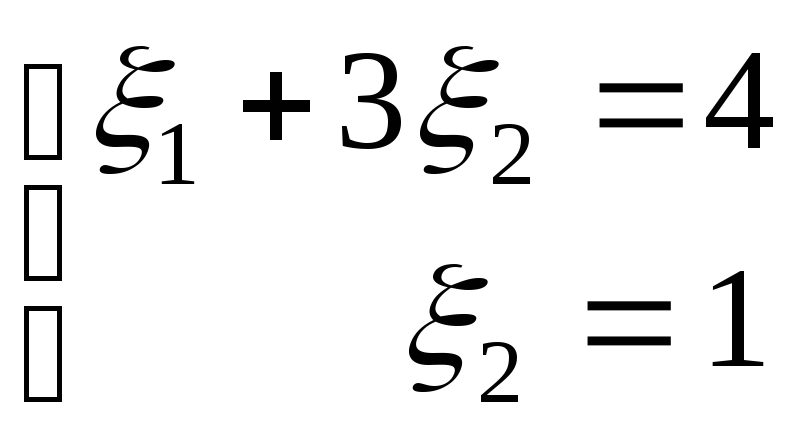Наконец, вычитая из первого уравнения 3 вторых, получаем систему уравнений

,

которая определяет единственное решение исходной системы

.

Теперь повторим проделанные преобразования на расширенной матрице исходной СЛАУ, заменяя каждое преобразование соответствующим строчным

элементарным преобразованием:

.

Заметим, что итогом проведённых преобразований явилось поученное из основной матрицы системы матрицы приведённого вида, которая в данном случае совпала с единичной матрицей . Кроме того, в данном случае правые части последней системы уравнений образуют единственное решение исходной системы.

Перейдём к изложению метода Гаусса в общем случае.

Элементарными преобразованиями СЛАУ называются: перемена местами двух её уравнений, умножение обеих частей какого-либо уравнения СЛАУ на число, отличное от нуля, добавление к левой и правой частям какого-либо уравнения соответственно левой и правой частей другого уравнения, умноженных на произвольное число.

Метод Гаусса решения СЛАУ состоит в последовательном выделении в каждом уравнении неизвестного, которое после этого элементарными преобразованиями СЛАУ исключается из всех её остальных уравнений.

Поскольку каждой СЛАУ вида (2.1) можно поставить в соответствие её расширенную матрицу (2.5) и это соответствие взаимооднозначно, т.е. каждая матрица вида (2.5) является расширенной матрицей некоторой СЛАУ, вместо элементарных преобразований СЛАУ удобно проводить строчные элементарные преобразования её расширенной матрицы. Нетрудно заметить, что после выделения в одном уравнении некоторого неизвестного (это неизвестное называется ведущим в данном уравнении) и последующего его исключения из остальных уравнений СЛАУ, соответствующая строка её основной матрицы будет иметь приведённый вид. Поэтому будем говорить, что и уравнение, отвечающее этой строке матрицы, имеет приведённый вид. Если же каждое уравнение СЛАУ, содержащее хотя бы один ненулевой коэффициент, имеет приведённый вид, будем говорить, что СЛАУ имеет приведённый вид.

Ясно, что в этом случае основная матрица СЛАУ тоже имеет приведённый вид.

Алгоритм метода Гаусса распадается на 3 этапа:

1. построение СЛАУ приведённого вида, равносильной исходной СЛАУ;

2. анализ СЛАУ приведённого вида;

3. описание общего решения.

Следующее предложение является обоснованием применимости метода Гаусса к любой СЛАУ.

Предложение 2.1. Для любой СЛАУ вида (2.1) существует равносильная ей СЛАУ приведённого вида.

◄ В силу предложения 1.3 найдётся конечное число строчных элементарных преобразований, применяя которые к матрице , мы получим матрицу приведённого вида. По свойству 5) элементарных преобразований существует такая матрица , что . Заметим, что матрица является произведением элементарных матриц, отвечающих указанным выше элементарным преобразованиям. Применив те же самые элементарные преобразования к расширенной матрице системы уравнений (2.1), получаем матрицу системы уравнений приведённого вида

.

Переходя к соответствующим матричным уравнениям и , замечаем, что в силу предложения 1.9 они равносильны. Следовательно, равносильны и отвечающие им системы уравнений. ►

Лекция VII.

План

2.3 Анализ СЛАУ приведённого вида и описание общего решения

2.4 Однородные СЛАУ

2.5 Решение матричных уравнений методом Гаусса

2.6 Отыскание обратной матрицы методом Гаусса