2.4 Однородные слау

Общий вид однородной СЛАУ, состоящей из уравнений с неизвестными, даётся формулами

Как уже отмечалось выше, однородная СЛАУ всегда совместна, так как имеет нулевое решение

.

Поэтому исследование такой СЛАУ сводится к выяснению существования у неё нулевого решения. Если нулевого решения не существует, однородная СЛАУ является определённой и подчиняется предложению 2.3. Если же ненулевое решение существует, то однородная СЛАУ является неопределённой и подчиняется предложению 2.4.

Следующие утверждения вытекают непосредственно из предложений 2.3 и 2.4.

Предложение 2.5. (Критерий определённости однородной СЛАУ). Для того, чтобы однородная СЛАУ была определённой, необходимо и достаточно, чтобы любая равносильная ей СЛАУ приведённого вида не содержала свободных неизвестных.

Предложение 2.6 .(Критерий существования у однородной СЛАУ ненулевого решения). Для того, чтобы однородная СЛАУ имела ненулевое решение, необходимо и достаточно, чтобы любая равносильная ей СЛАУ приведённого вида имела свободные неизвестные.

Если последнее условие выполнено, СЛАУ имеет бесконечное множество решений, зависящее от произвольных постоянных , количество которых совпадает с числом свободных неизвестных.

Приведём ещё одно достаточное условие для существования у однородной СЛАУ ненулевого решения.

Предложение 2.7. Если число уравнений однородной СЛАУ меньше числа её неизвестных , тогда СЛАУ имеет ненулевое решение.

◄ Если , тогда, как следует из метода Гаусса, можно построить СЛАУ приведённого вида, равносильную исходной СЛАУ, у которой число уравнений не превосходит . Следовательно, у этой СЛАУ приведённого вида число уравнений также меньше числа неизвестных. Так как каждое уравнение этой СЛАУ, имеющее хотя бы один ненулевой коэффициент, имеет точно одну связанную неизвестную, то у приведённой СЛАУ обязательно будут свободные неизвестные. Остаётся применить предложение 2.6. ►

2.5 Решение матричных уравнений методом Гаусса

Рассмотрим матричное уравнение

(2.8)

в предложении, что . В силу предложения 1.7 единственное решение этого уравнения имеет вид

В то же время матричное уравнение (2.8) ввиду правила умножения матриц эквивалентно системе матричных уравнений

, (2.9)

каждое из которых, являясь уравнением типа (2.6), равносильно определённой СЛАУ с расширенной матрицей

. (2.10)

Единственное решение этой системы уравнений имеет вид

,

и, как следует из 2.4, получается в результате приведения основной матрицы системы к виду ,

.

Однако, ничто не мешает нам решать системы уравнений с матрицами вида (2.10) одновременно для всех значений . Вводя расширенную матрицу и приводя строчными элементарными преобразованиями основную матрицу к виду , мы получим, что

.

На практике обычно возникает более общая задача решения матричного уравнения (2.8) для произвольных матриц , , . Изложенное выше позволяет сформулировать следующий алгоритм решения этой задачи.

Составляем матрицу и строчными элементарными преобразованиями приводим её к виду , где – приведённая матрица, л‑эквивалентная матрице .

1) Если (в этом случае, конечно, – квадратная матрица), уравнение (2.8) разрешимо для любой , а – его единственное решение.

2) Если , тогда для разрешимости уравнений (2.8) необходимо и достаточно, чтобы у матрицы не было нулевых строк, либо при наличии нулевой строки, например, выполнялось условие (для каждой такой строки).

3) Если и уравнение (2.8) разрешимо, то для того, чтобы его решение было единственным, необходимо и достаточно, чтобы у приведённой СЛАУ с матрицей не было свободных неизвестных. Если последнее условие нарушено, то уравнение (2.8) имеет бесчисленное множество решений, а его общее решение определяется способом, описанным в пункте 2.4.

Пример 5. Решить матричное уравнение (2.8), если

.

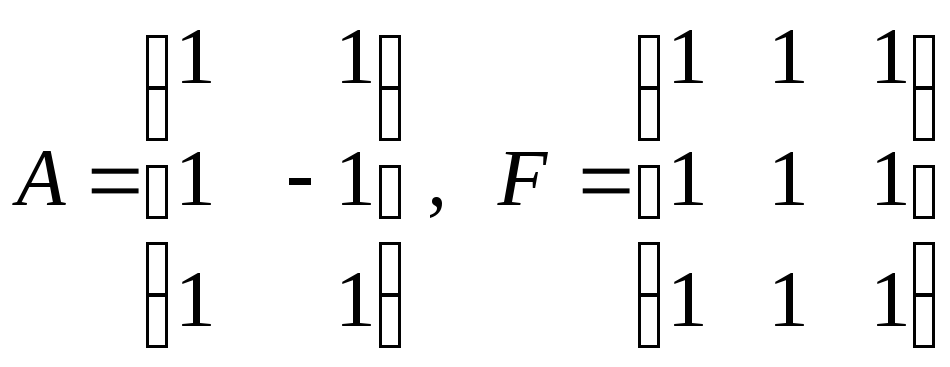◄ Применяя метод Гаусса к расширенной матрице , получаем, что

.

Откуда следует, что матрица и , то есть уравнение (2.8) разрешимо. Так как у приведённой СЛАУ нет свободных переменных, то его решение единственно и имеет вид

. ►

Предлагаем читателю самостоятельно убедиться, что уравнение (2.8) с той же самой матрицей , но с другой правой частью

неразрешимо.

Пример 6. Решить матричное уравнение (2.8), если

.

◄ Применяя метод Гаусса к расширенной матрице , получаем, что

. (2.11)

Откуда следует, что матрица и не имеет нулевых строк, но у приведённой СЛАУ есть одна свободная неизвестная . Таким образом, уравнение (2.8) разрешимо и имеет бесчисленное множество решений. Общее решение находим из системы (2.11), определяя и соответственно из систем и . Именно полагая из системы

или

получаем, что

.

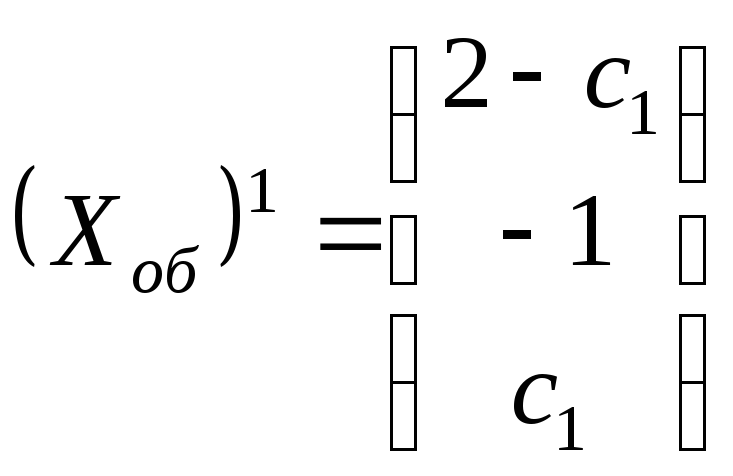Полагая из системы

или

получаем, что

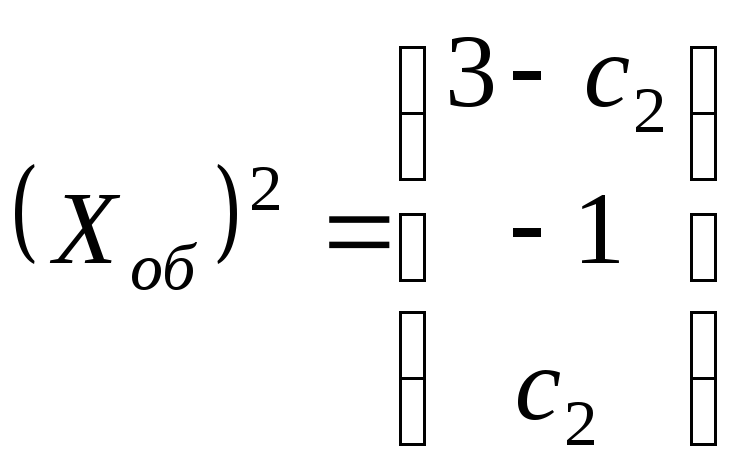, то есть .

Наконец, заметим, что матричное уравнение вида

применением к нему операции транспонирования сводится к уравнению вида (2.8)

.

Оба эти уравнения разрешимы или неразрешимы одновременно, а их решения взаимнотранспонированны. ►