2.3 Анализ слау приведённого вида

Исследование СЛАУ приведённого вида распадается на три случая.

1)Система уравнений приведённого вида содержит “плохое” уравнение, т.е. уравнение вида

, (2.7)

где . Так как это уравнение не имеет решений, система уравнений приведённого вида, а с ней и исходная система уравнений несовместны.

Пример 2. Решить СЛАУ методом Гаусса и найти её общее решение

.

◄ Переходя к матричной записи системы и применяя подходящие строчные элементарные преобразования, получаем систему приведённого вида, равносильную исходной системе уравнений:

.

Мы остановили процесс получения системы приведённого вида, так как последняя система (а с ней и исходная система) уравнений несовместна. ►

2) Система уравнений приведённого вида не содержит “плохих” уравнений. Все неизвестные в системе уравнений приведённого вида делим на две группы: неизвестные, являющиеся ведущими в своих уравнениях, называем связанными, а остальные неизвестные – свободными. (Случай отсутствия свободных неизвестных рассмотрим отдельно). Объявляя свободные неизвестные параметрами и т.д., принимающими произвольные действительные значения, выражаем связанные неизвестные через свободные. Полученные в результате этого формулы определяют общее решение СЛАУ. Если свободным неизвестным придать конкретные значения, а после этого вычислить по найденным формулам значения связанных неизвестных, мы получаем некоторое частное решение рассматриваемой системы уравнений.

Таким образом, в данном случае система уравнений приведённого вида, а с нею и исходная система уравнений совместны, неопределенны и имеют бесчисленное множество решений.

Пример 3. Следующую систему уравнений решить методом Гаусса, найти её общее и одно частное решения

.

◄ По аналогии с предыдущим примером

.

Полученная система уравнений имеет приведённый вид и не имеет “плохих” уравнений. Её свободными неизвестными являются и , а связанными неизвестными и . Полагая , находим и из уравнений приведённой системы,

.

Из второго уравнения , из первого уравнения . Поэтому общее решение рассматриваемой системы уравнений имеет вид

.

Полагая и равными, например, 1, получаем частное решение

. ►

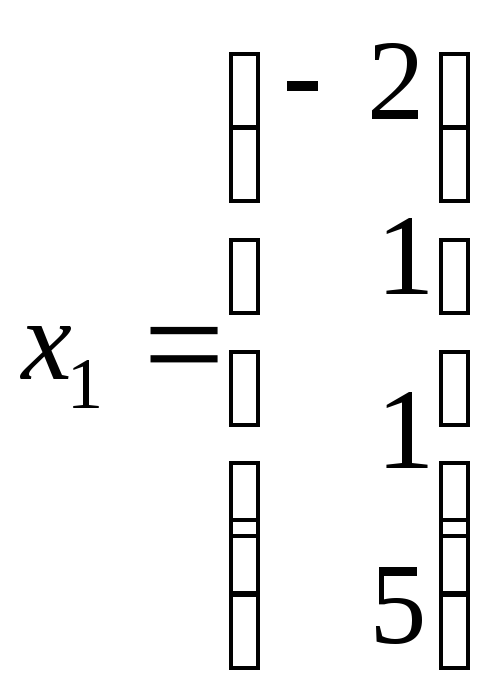Замечание. В случае неопределённых СЛАУ выбор свободных и связанных неизвестных осуществляется неоднозначно и зависит от элементарных преобразований, применённых в алгоритме Гаусса. В связи с этим и общее решение таких систем уравнений может иметь различную форму.

3) Система уравнений приведённого вида не содержит “плохих” уравнений и свободных неизвестных. Поскольку в этом случае все неизвестные связанные, расширенная матрица приведённой СЛАУ, возможно, после перемены местами некоторых уравнений принимает вид

.

Ясно, что данная система уравнений является определённой, а е единственное решение имеет вид

.►

Пример 4. Следующую систему уравнений решить методом Гаусса

.

◄ Находим расширенную матрицу системы приведённого вида, равносильной данной системе уравнений:

.

Полученная приведённая система уравнений является определённой, а её единственное решение имеет вид

. ►

Итоги изучения систем линейных алгебраических уравнений методом Гаусса сформулируем в виде ряда предложений.

Предложение 2.2. (Критерий совместности СЛАУ). Для того, чтобы СЛАУ была совместной, необходимо и достаточно, чтобы любая равносильная ей СЛАУ приведённого вида не содержала уравнений вида (2.7).

Предложение 2.3. (Критерий определённости СЛАУ). Для того, чтобы СЛАУ была определённой, необходимо и достаточно, чтобы любая равносильная ей СЛАУ приведённого вида не содержала уравнений вида (2.7) и свободных неизвестных.

Предложение 2.4. (Критерий неопределённости СЛАУ). Для того, чтобы СЛАУ была неопределённой, необходимо и достаточно, чтобы любая равносильная ей СЛАУ приведённого вида не содержала уравнений вида (2.7) и имела свободные неизвестные.

Если последние два условия выполнены, СЛАУ имеет бесконечное множество решений, зависящее от произвольных постоянных , количество которых совпадает с числом свободных неизвестных.