1.3. Язык блок-схем для представления алгоритмов

Существует несколько способов представления алгоритмов. Мы рассмотрим язык блок-схем, это наиболее простой и наглядный способ, пригодный для алгоритмов любой сложности.

Блок-схема - это графическое представление алгоритма, где все инструкции пишутся в некоторых геометрических фигурах, я стрелками указывается последовательность выполнения операций.

Рассмотрим составляющие блок-схему блоки.

Операторы ввода и вывода помещаются в параллелограмм (см. рис. 2 а).

Если это оператор ввода, то после его выполнения, все перечисленные в нем переменные получат значения, введенные в момент выполнения алгоритма с устройства ввода. Если это оператор вывода, то в момент выполнения алгоритма, на устройство вывода будут выведены взятые из памяти значения переменных, перечисленных в операторе.

Вычислительные операторы записываются в прямоугольных блоках (рис. 2 б).

В названные блоки может входить сколько угодно стрелок и выходить - только одна.

Следующий блок в виде ромба (рис. 2 в) имеет две выходящие стрелки, но это не нарушает однозначности алгоритма, т.к. в таком блоке записывается условие и, в зависимости от результата его проверки, выполнение алгоритма продолжается по стрелке с надписью “да”, если условие выполнено, или - с надписью “нет”, если условие не выполнено.

И наконец в овале записывается оператор STOP, останавливающий процесс вычисления.

Блок-схема алгоритма может состоять из любого числа блоков, только для наглядности они должны помещаться на одной странице. Блок схемы рисуют сверху вниз и, если есть стрелки идущие вверх, то на них не должно быть блоков.

1.4. Базовые структуры алгоритмов

Наложим еще некоторые ограничения на структуру блок-схемы. Будем строить алгоритм, используя только три фрагмента определенной конфигурации. Назовем их базовыми структурами алгоритмов.

Первая базовая структура - следование состоит из цепочки блоков без разветвлений.

Вторая базовая структура - ветвление имеет вид, представленный на рис. 3. Смысл этой конструкции состоит в выборе, в зависимости от результатов проверки условия, одной из двух альтернативных групп операторов S или P, либо, в частном случае, - выполнение или невыполнение группы операторов R.

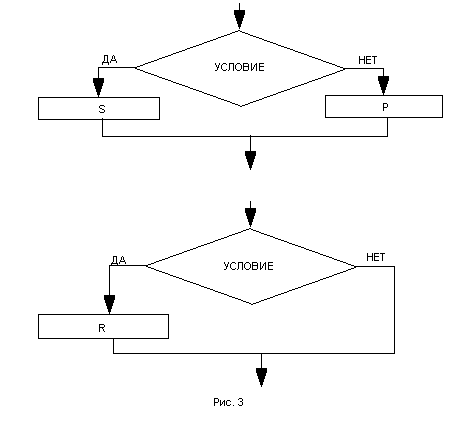
Третья базовая структура - цикл.

Смысл цикла в многократном выполнении группы операторов, называемых телом цикла. Для завершения работы цикла необходимо осуществить проверку некоторого условия выхода из цикла. В зависимости от того, расположена ли эта проверка до тела цикла или после него, различают цикл с предусловием (рис. 4 а) и цикл с постусловием (рис. 4б).

Важной особенностью всех этих структур является наличие одного входа и одного выхода. Это дает возможность вкладывать одни базовые конструкции в другие, т.е. строить иерархию таких структур. При этом некоторый прямоугольный блок заменяется одной из базовых структур.

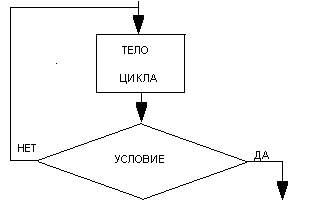
Рис. 4 а)

Рис. 4 б)

Рассмотрим пример простейшего циклического алгоритма. Пусть надо посчитать факториал числа N. Как известно факториал числа N равен произведению всех целых положительных чисел меньших и равных числу N, т.е. N! = 1*2*...*N. Ясно, что для подсчета факториала необходимо многократно повторять умножение, следовательно, алгоритм должен содержать цикл. Конструируя алгоритм надо выбрать структуру цикла с предусловием или с постусловием. Перед циклом следует поставить блоки подготовки цикла, в них задаются начальные значения переменных, встречающихся в правой части операторов тела цикла. Естественно в начале алгоритма необходимо ввести исходные данные, в рассматриваемом примере - значение числа N.

На рис. 5 представлены блок схемы алгоритма подсчета факториала числа N.

На рис. 5 использован цикл с предусловием, а на рис.6. - с постусловием.

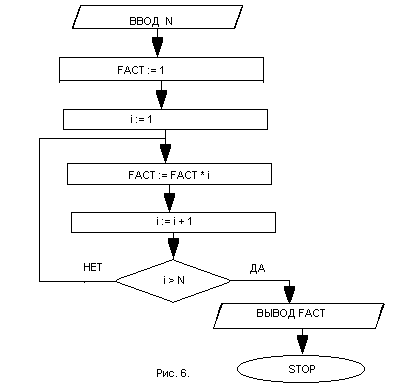
В обоих алгоритмах переменная i содержит текущий сомножитель для подсчета факториала, с точки зрения структуры цикла i это параметр цикла. Блок, находящийся в теле цикла и содержащий оператор i := i + 1, подготавливает следующий шаг выполнения тела цикла. Для этого к значению переменной i прибавляется единица (правая часть оператора) и полученное новое значение приписывается переменной i, т.е. значение переменной i изменяется на единицу.