3.3.1. Розв’язок типових прикладів завдань 6, 7 ргр

1. Привести до канонічного виду рівняння кола . Знайти координати його центра і радіус. Побудувати коло.

Розв’язок. Приведемо рівняння кола до канонічного виду: додамо і віднімемо з нього квадрати половин

коефіцієнтів при невідомих і ,

тобто і , а

потім виділимо повні квадрати

;

,

Отже, центр кола знаходиться

в точці , а радіус .

Відповідь: .

2. Скласти рівняння геометричного місця точок, відношення відстаней яких до точки та до прямої дорівнює числу . Отримане рівняння привести до канонічного виду. Знайти півосі і , координати фокусів і побудувати криву.

Розв’язок. Побудуємо точку і пряму . Нехай довільна точка шуканого геометричного місця точок. Опустимо перпендикуляр на прямую і визначимо координати точки . Так як точка лежить на вказаній прямій, то її абсциса дорівнює 6, а ордината – ординаті точки (рис. 3.10). За умовою задачі .

; .

Підведемо обидві частини останньої рівності в квадрат:

– канонічне рівняння еліпса.

; ;

Рис. 3.10

Відповідь: Еліпс ; , ;

3. Скласти канонічне рівняння геометричного місця точок, відношення відстаней яких до точки та до прямої дорівнює . Знайти координати фокусів , вершин ; ексцентриситет , і рівняння асимптот кривої. Визначити точки перетину кривої з колом, центр якого знаходиться в початку координат, а коло проходить через її фокуси. Побудувати асимптоти, криву і коло.

Розв’язок. 1) Побудуємо точку і пряму . Нехай довільна точка шуканого геометричного місця точок (рис.3.11).

З’єднаємо точки і , а потім проведемо перпендикуляр до прямої . Так як точка лежить на вказаній прямій, то її абсциса , а ордината дорівнює ординаті точки , тобто .

За умовою задачі _{Отримуємо:}

; .

Підведемо обидві частини отриманої рівності в квадрат і виконаємо перетворення:

– канонічне рівняння гіперболи.

Значить, півосі гіперболи: ;

Знайдемо координати фокусів гіперболи і радіус кола

.

Визначимо координати вершин гіперболи ; .

Обчислимо ексцентриситет гіперболи: .

Знайдемо рівняння асимптот ; .

Запишемо рівняння кола .

Для знаходження точок перетину кола з гіперболою розв’яжемо систему рівнянь:

.

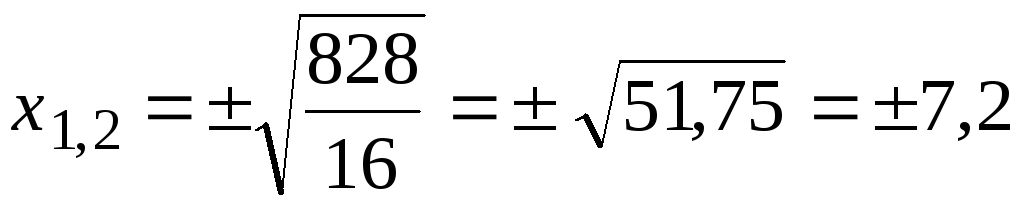Підставляючи отримане значення в рівняння кола, знаходимо:

.

Побудуємо коло і гіперболу

Рис. 3.11

4. Привести рівняння кривої до канонічного виду. Найти параметр кривої, координати вершини , фокуса и рівняння директриси. Побудувати криву і її директрису.

Привести рівняння кривої до канонічного вигляду. Знайти параметр кривої, координати вершини , фокуса і рівняння директриси. Побудувати криву і її директрису.

Розв’язок. Додамо і віднімемо в лівій частині рівняння квадрат половини коефіцієнта перед і перетворимо отримане рівняння

.

Порівнюючи отримане рівняння з канонічним рівнянням параболи (3.34) , находимо ; ; .

Координати фокуса визначаються, як

; , тобто .

Рівняння директриси ; .

Рис.3.12