Умова паралельності прямих

або . (3.14)

Умова перпендикулярності прямих

або . (3.15)

2. Точка перетину двох прямих, заданих загальними рівняннями

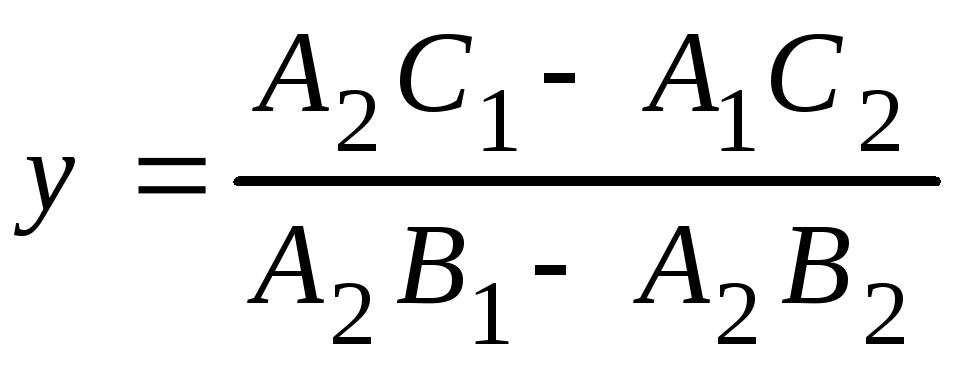; . (3.16)

3. Рівняння пучка прямих.

Пучком прямих, які проходять через задану точку , називають сукупність всіх прямих, які проходять через цю точку

. (3.17)

Рівняння пучка прямих, що проходять через точку перетину двох прямих має вигляд

. (3.18)

Тут параметр невизначений.

4. Відстань від заданої точки до прямої

. (3.19)

3.2.1. Розв’язок типових прикладів завдання 5 ргр

Задано координати вершин трикутника : , , . Знайти: 1) довжину сторони ; 2) рівняння сторін і ВС та їх кутові коефіцієнти; 3) кут в градусах; 4) рівняння висоти і її довжину; 5) рівняння медіани і координати точки , перетину цієї медіани з висотою ; 6) рівняння прямої , яка проходить через точку , паралельно стороні .

Розв’язок. 1. Відстань між точками і дорівнює

.

В нашому випадку , і довжина сторони

15 Од. Довжини.

2. Запишемо рівняння прямої, яка проходить через і

; . .

Розв’язавши останнє рівняння відносно у, знаходимо:

; , звідки .

Підставивши в (3.10) координати точок і , отримаємо рівняння :

; .

Шуканий утворюється прямими і , кутові коефіцієнти яких , , , . Підставивши значення кутових коефіцієнтів в (3.12), отримаємо

; рад , або .

4. Висота перпендикулярна стороні . Щоб знайти її кутовий коефіцієнт, скористаємося умовою перпендикулярності прямих

.

Підставивши в рівняння пучка прямих (3.23) координати точки і знайдений кутовий коефіцієнт, отримаємо рівняння висоти :

.

Довжину висоти знайдемо, як відстань від до прямої за формулою (3.19), де , , , ,

(од. довжини).

5. Знайдемо координати точки , яка належить медіані :

.

Підставивши в (3.10) координати точок і , знаходимо рівняння медіани:

; .

Координати точки перетину висоти і медіани знайдемо, вважаючи, що в даному випадку , , ; , ,

; ; .

6. Так як шукана пряма паралельна стороні , то її кутовий коефіцієнт дорівнює кутовому коефіцієнту прямої _:

.

Трикутник , висота , медіана , пряма побудовані в системі координат на рис.3.4.

Рис. 3.4

3.3. Криві другого порядку в прямокутній системі координат

Колом називають геометричне місце точок, рівновіддалених від даної точки, яка називається центром кола.

Канонічне рівняння кола має вигляд

, (3.20)

де координати її центра, радіус кола.

Еліпсом називається геометричне місце точок, сума відстаней яких до двох даних точок цієї площини, які називаються фокусами, є величина стала і більша відстані між фокусами , const (рис. 3.5).

Рис. 3.5

Канонічне рівняння еліпса має вигляд

, (3.21)

де велика і мала півосі еліпса.

Якщо , то фокуси еліпса розташовані на осі , їх координати ; і фокусна відстань зв’язана з півосями еліпса співвідношенням . (3.22)

Еліпс перетинає вісь в точках , , вісь в точках , . Ці точки називаються вершинами еліпса. Величини і називаються відповідно великою і малою осями еліпса.

Міра відхилення еліпса від кола характеризується величиною , яка називається ексцентриситетом еліпса і дорівнює відношенню його фокусної відстані до довжини великої півосі

. (3.23)

Оскільки у еліпса , то ексцентриситет еліпса .

Чим менше значення , тим ближче еліпс за формою до кола.

Директрисами еліпса називаються прямі , які паралельні його малій осі і віддалені від неї на відстані .

Гіперболою називається геометричне місце точок, абсолютна величина різниці відстаней яких до двох даних точок площини, що називаються фокусами, є величина стала і менша відстані між фокусами , const (рис. 3.6).

Рис. 3.6

Канонічне рівняння гіперболи має вигляд:

, (3.24)

де дійсна піввісь; уявна піввісь гіперболи.

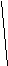
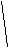
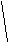Точка рухаючись по гіперболі, нескінченно віддаляючись від вершини, необмежено наближається до однієї з прямих, які проходять через центр симетрії, і називаються асимптотами гіперболи.

Рівняння асимптот гіперболи . (3.25)

Якщо фокуси гіперболи розташовані на осі , то їх координати і , і фокусна відстань зв’язана з дійсною і уявною півосями співвідношенням . (3.26)

Гіпербола перетинає вісь в точках , . Ці точки називаються вершинами гіперболи.

Ексцентриситетом гіперболи називається відношення фокусної відстані гіперболи до її дійсної півосі

. (3.27)

Оскільки у гіперболи , то ексцентриситет гіперболи .

Директрисами гіперболи називаються прямі , паралельні уявній осі і віддалені від неї на відстані .

Параболою називається геометричне місце точок, рівновіддале-них від даної точки, яка називається фокусом і від даної прямої, яка називається директрисою і не проходить через фокус (рис. 3.7).

Рис. 3.7.

Канонічне рівняння параболи, віссю симетрії якої є вісь а вершина співпадає з початком координат, має вигляд:

, (3.28)

де параметр параболи, рівній відстані від фокуса до директриси.

Фокальний радіус довільної точки параболи обчислюється за формулою

. (3.29)

Ексцентриситет параболи дорівнює відношенню відстані довільної її точки до фокуса та до відповідної директриси. На підставі визначення, ексцентриситет параболи дорівнює одиниці .

Рівняння , , є канонічним рівнянням параболи з вітками, що направлені вгору (рис. 3.24, а), а рівняння , – рівнянням параболи, з вітками, що направлені вниз(рис. 3.8, б).

Рис. 3.8

Парабола, канонічне рівняння якої , , симетрична осі і розташована справа від осі , , (рис. 3.8, в), а парабола , – зліва від осі (рис. 3.8, г).

Якщо парабола симетрична прямій, паралельній осі , а координати вершини параболи , то рівняння має вигляд:

. (3.30)