
- •3. Аналітична геометрія на площині|площині| …………………….. 23
- •1. Лінійна алгебра
- •1.1. Визначники. Обчислення|підрахунок| визначників
- •1.2. Матриці і їх властивості
- •1.3. Розв’язок систем лінійних рівнянь
- •1.4. Розв’язок типового прикладу|зразків| завдання|задавання| 1 ргр
- •2. Векторна алгебра
- •2.1. Векторні і скалярні величини. Розкладання вектора за координатними осями
- •2.2. Скалярний добуток двох векторів
- •. Умова паралельності і перпендикулярності векторів
- •. Механічний зміст скалярного добутку
- •2.2.1. Розв’язок типового прикладу завдання 2 ргр
- •Знайдемо косинус кута між векторами за формулою
- •2.3. Векторний добуток двох векторів
- •2.3.1. Розв’язок типового прикладу завдання 3 ргр
- •2.4. Мішаний добуток трьох векторів
- •2.4.1. Розв’язок типового прикладу завдання 4 ргр
- •Тоді об’єм тетраедра
- •3.1. Довжина і напрям відрізка. Поділ відрізка в заданому відношенні. Площа трикутника
- •3.2. Пряма лінія на площині
- •. Рівняння прямої з заданим кутовим коефіцієнтом
- •. Рівняння прямої в відрізках на осях
- •Умова паралельності прямих
- •2. Точка перетину двох прямих, заданих загальними рівняннями
- •3. Рівняння пучка прямих.
- •3.2.1. Розв’язок типових прикладів завдання 5 ргр
- •15 Од. Довжини.
- •3.3. Криві другого порядку в прямокутній системі координат
- •3.3.1. Розв’язок типових прикладів завдань 6, 7 ргр
- •3.4. Криві другого порядку в полярній системі координат. Параметричні рівняння плоских кривих
- •Деякі типи кривих на площині, заданих
- •4. Аналитическая геометрия в пространстве
- •4.1. Плоскость
- •4. Аналітична геометрія в просторі
- •4.1. Площина . Основні рівняння площини
- •Загальне рівняння площини
- •3. Де відрізки, які відтинає площина на координатних осях
- •3. Умова паралельності площин
- •4.1.1. Розв’язок типового прикладу завдання 8 ргр
- •4.2. Пряма лінія в просторі. Взаємне розташування прямої і площини
- •4.2.1. Розв’язок типових прикладів завдань 9, 10 ргр
- •Завдання до розрахунково-графічної роботи Завдання 1
- •Завдання 2
- •Завдання 3
- •Завдання 4
- •Завдання 5
- •Завдання 6
- •Завдання 7
- •Завдання 8
- •Завдання 9
- •Завдання 10
- •ФормулИ з ЕлементарноЇ математикИ
- •7. Формули подвійного кута
- •8. Формули зниження степені
- •9. Відношення в довільному трикутнику
- •Додаток 4 Номери індивідуальних завдань Дві останні цифри номера залікової книжки
- •Дві останні цифри номера залікової книжки
2.4.1. Розв’язок типового прикладу завдання 4 ргр
П риклад
2.3. Обчислити об’єм тетраедра
риклад
2.3. Обчислити об’єм тетраедра
![]()
і площу грані
![]() ,
якщо
,
якщо![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Розв’язок. Зробимо схематичний рисунок
(2.7). Об’єм тетраедра, згідно (2.18)
 .
.
Знайдемо вектори
![]() ;
;
![]() ;
;
![]() .
.
Тоді об’єм тетраедра

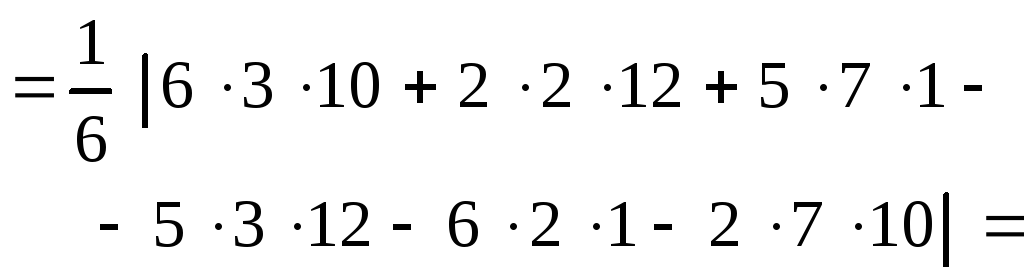
= (куб. од.).
(куб. од.).
Площа грані
![]() дорівнює половині площі паралелограма,
побудованого на векторах
дорівнює половині площі паралелограма,
побудованого на векторах
![]() і
і
![]() .
Позначимо векторний добуток
.
Позначимо векторний добуток
![]() через
через
![]() .
Тоді модуль вектора
.
Тоді модуль вектора
![]() дорівнює площі паралелограма
дорівнює площі паралелограма


![]() .
.

![]() (кв. од.).
(кв. од.).
Відповідь:
![]() куб. од.;
куб. од.;
![]() кв. од.
кв. од.
3.1. Довжина і напрям відрізка. Поділ відрізка в заданому відношенні. Площа трикутника
![]()
 Довжина відрізка на площині
Довжина відрізка на площині
(рис. 3.1), заданого координатами свого
початку
![]() і кінця
і кінця
![]() дорівнює
дорівнює
![]() .
(3.1)
.
(3.1)
Якщо початок відрізка співпадає з
початком координат, то формула (3.1)
має вигляд
![]() . (3.2)
. (3.2)
![]() Нехай
Нехай
![]() і
і
![]() – кути, які утворює відрізок з додатними
напрямами осей
– кути, які утворює відрізок з додатними
напрямами осей
![]() і
і
![]() ,
тоді напрями відрізка визначаються
завданням косинусів їх кутів
,
тоді напрями відрізка визначаються
завданням косинусів їх кутів
 ;
;
 (3.3)
(3.3)
![]() Координати точки
Координати точки
![]() ,
яка ділить відрізок
,
яка ділить відрізок
![]() в відношенні
в відношенні
 ,
знаходяться за формулами
,
знаходяться за формулами
 ;
;
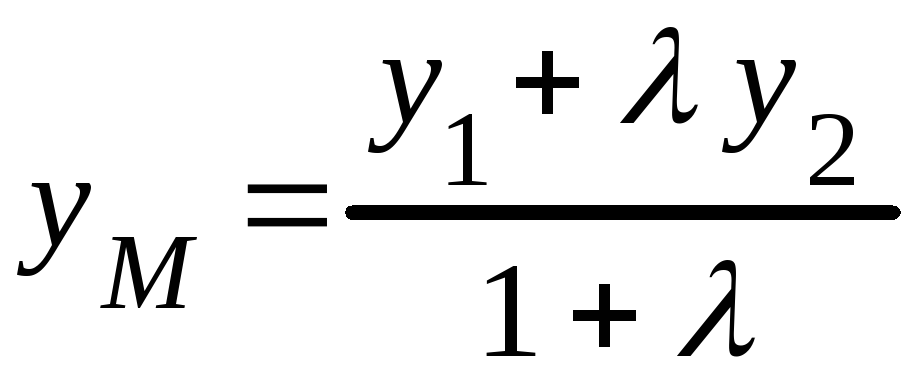 . (3.4)
. (3.4)
Якщо точка
![]() ділить відрізок
ділить відрізок
![]() пополам, то
пополам, то
![]() і координати точки
і координати точки
![]() дорівнюють
дорівнюють
 ;
;
 . (3.5)
. (3.5)
Якщо
![]() число від’ємне, то точка
число від’ємне, то точка
![]() знаходиться на продовженні відрізка
знаходиться на продовженні відрізка
![]() і поділ називається зовнішнім.
і поділ називається зовнішнім.
![]() Площа трикутника з вершинами
Площа трикутника з вершинами
![]() ,
,
![]() ,
,
![]() обчислюється за формулою
обчислюється за формулою
 . (3.6)
. (3.6)
Оскільки площа трикутника – величина додатна, то права частина формули (3.6) береться за абсолютною величиною.
3.2. Пряма лінія на площині
Пряму лінію на площині відносно системи прямокутних декартових координат можна задати різними способами і в результаті отримати різні види рівняння прямої.
![]() .
Загальним
рівнянням
прямої
на площині
називається рівняння виду
.
Загальним
рівнянням
прямої
на площині
називається рівняння виду
![]() . (3.7)
. (3.7)
. Рівняння прямої з заданим кутовим коефіцієнтом

![]() ,
(3.8)
,
(3.8)
д
Рис. 3.1![]() кутовий коефіцієнт прямої,
кутовий коефіцієнт прямої,
![]() кут нахилу прямої до додатного напря-
кут нахилу прямої до додатного напря-
му осі
![]() ,
,
![]() величина відрізка, який
величина відрізка, який
відтинає пряма на осі
![]() (рис.3.2).
(рис.3.2).
. Рівняння прямої в відрізках на осях
 ,
(3.9)
,
(3.9)
де
![]() відрізки, які відтинає пряма на осях
координат (рис. 3.2).
відрізки, які відтинає пряма на осях
координат (рис. 3.2).
Рис. 3.1![]() .
.
![]() и
и
![]()
![]() . (3.10)
. (3.10)
![]() .
Нормальне рівняння прямої
.
Нормальне рівняння прямої
![]() , (3.11)
, (3.11)
де
![]() довжина перпендикуляра, опущеного на
пряму з початку координат,
довжина перпендикуляра, опущеного на
пряму з початку координат,
![]() кут, який відраховується від додатного
напряму осі
кут, який відраховується від додатного
напряму осі
![]() проти
проти
годинникової стрілки до перпендикуляра
![]() (рис. 3.2).
(рис. 3.2).
![]() .
Основні задачі для прямої лінії
.
Основні задачі для прямої лінії
1. Якщо прямі задані загальними рівняннями
![]() і
і
![]() ,
то кут між цими прямими знаходиться
за формулою
,
то кут між цими прямими знаходиться
за формулою
 .
(3.12)
.
(3.12)
Якщо прямі задані рівняннями
![]()

![]() и
и
![]() ,
,
![]()
(рис. 3.3) то формула (3.12) має вигляд
 ,
(3.13)
,
(3.13)
де
![]() ,
,
![]() ,
,
![]() кут, який
кут, який
відраховується від прямої
![]() до прямої
до прямої
![]() за годинниковою стрілкою.
за годинниковою стрілкою.
