
- •3. Аналітична геометрія на площині|площині| …………………….. 23
- •1. Лінійна алгебра
- •1.1. Визначники. Обчислення|підрахунок| визначників
- •1.2. Матриці і їх властивості
- •1.3. Розв’язок систем лінійних рівнянь
- •1.4. Розв’язок типового прикладу|зразків| завдання|задавання| 1 ргр
- •2. Векторна алгебра
- •2.1. Векторні і скалярні величини. Розкладання вектора за координатними осями
- •2.2. Скалярний добуток двох векторів
- •. Умова паралельності і перпендикулярності векторів
- •. Механічний зміст скалярного добутку
- •2.2.1. Розв’язок типового прикладу завдання 2 ргр
- •Знайдемо косинус кута між векторами за формулою
- •2.3. Векторний добуток двох векторів
- •2.3.1. Розв’язок типового прикладу завдання 3 ргр
- •2.4. Мішаний добуток трьох векторів
- •2.4.1. Розв’язок типового прикладу завдання 4 ргр
- •Тоді об’єм тетраедра
- •3.1. Довжина і напрям відрізка. Поділ відрізка в заданому відношенні. Площа трикутника
- •3.2. Пряма лінія на площині
- •. Рівняння прямої з заданим кутовим коефіцієнтом
- •. Рівняння прямої в відрізках на осях
- •Умова паралельності прямих
- •2. Точка перетину двох прямих, заданих загальними рівняннями
- •3. Рівняння пучка прямих.
- •3.2.1. Розв’язок типових прикладів завдання 5 ргр
- •15 Од. Довжини.
- •3.3. Криві другого порядку в прямокутній системі координат
- •3.3.1. Розв’язок типових прикладів завдань 6, 7 ргр
- •3.4. Криві другого порядку в полярній системі координат. Параметричні рівняння плоских кривих
- •Деякі типи кривих на площині, заданих
- •4. Аналитическая геометрия в пространстве
- •4.1. Плоскость
- •4. Аналітична геометрія в просторі
- •4.1. Площина . Основні рівняння площини
- •Загальне рівняння площини
- •3. Де відрізки, які відтинає площина на координатних осях
- •3. Умова паралельності площин
- •4.1.1. Розв’язок типового прикладу завдання 8 ргр
- •4.2. Пряма лінія в просторі. Взаємне розташування прямої і площини
- •4.2.1. Розв’язок типових прикладів завдань 9, 10 ргр
- •Завдання до розрахунково-графічної роботи Завдання 1
- •Завдання 2
- •Завдання 3
- •Завдання 4
- •Завдання 5
- •Завдання 6
- •Завдання 7
- •Завдання 8
- •Завдання 9
- •Завдання 10
- •ФормулИ з ЕлементарноЇ математикИ
- •7. Формули подвійного кута
- •8. Формули зниження степені
- •9. Відношення в довільному трикутнику
- •Додаток 4 Номери індивідуальних завдань Дві останні цифри номера залікової книжки
- •Дві останні цифри номера залікової книжки
2.2.1. Розв’язок типового прикладу завдання 2 ргр
Знайти внутрішні кути
![]() ,
,
![]() і
і
![]() трикутника, заданого вершинами
трикутника, заданого вершинами
![]() ,
,
![]() ,
,
![]() і переконатися, що їх сума дорівнює
і переконатися, що їх сума дорівнює
![]() .
.
Розв’язок. Знайдемо координати
векторів
![]() ,
,
![]() ,
,
![]() ,
і протилежні їм вектори
,
і протилежні їм вектори
![]() ,
,
![]() ,
,
![]() ,
враховуючи, що координати останніх
мають знаки, протилежні координатам
основних векторів
,
враховуючи, що координати останніх
мають знаки, протилежні координатам
основних векторів
![]() .
.
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Обчислимо довжини сторін трикутника
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
Знайдемо косинус кута між векторами за формулою
![]() .
.

![]()
![]() .
.

![]()
![]() .
.

![]()
![]() .
.
Перевірка:
![]() .
.
Відповідь:
![]() ;
;
![]() ;
;
![]() .
.
2.3. Векторний добуток двох векторів
Трійка не компланарних
векторів
![]() називається правою,
якщо при обертанні буравчика в напрямі
від вектора
називається правою,
якщо при обертанні буравчика в напрямі
від вектора
![]() до вектора
до вектора
![]() напрям поступального руху буравчика
утворює гострий кут з напрямом вектора
напрям поступального руху буравчика
утворює гострий кут з напрямом вектора
![]() .
Якщо ж кут тупий, то трійка називається
лівою.
.
Якщо ж кут тупий, то трійка називається
лівою.
![]() .
Векторним
добутком
двох векторів
.
Векторним
добутком
двох векторів
![]() називається вектор
називається вектор
![]() ,
який задовольняє наступним умовам:
,
який задовольняє наступним умовам:
1) довжина вектора
![]() дорівнює
дорівнює
![]() ,
де
,
де
 ;
(2.11)
;
(2.11)
2) вектор
![]() перпендикулярний
до кожного з векторів, тобто
перпендикулярний
до кожного з векторів, тобто
![]() і
і
![]() ;
;
3) вектор
![]() ,
має такий напрям, що вектори
,
має такий напрям, що вектори
![]() ,
,
![]() і
і
![]() утворюють праву трійку векторів.
Векторний добуток позначають одним із
символів:
утворюють праву трійку векторів.
Векторний добуток позначають одним із
символів:
![]() .
.
![]() .
Якщо вектори задані
проекціями на осі координат
.
Якщо вектори задані
проекціями на осі координат
![]() і
і
![]() ,
то векторний добуток визначається
за формулою
,
то векторний добуток визначається
за формулою
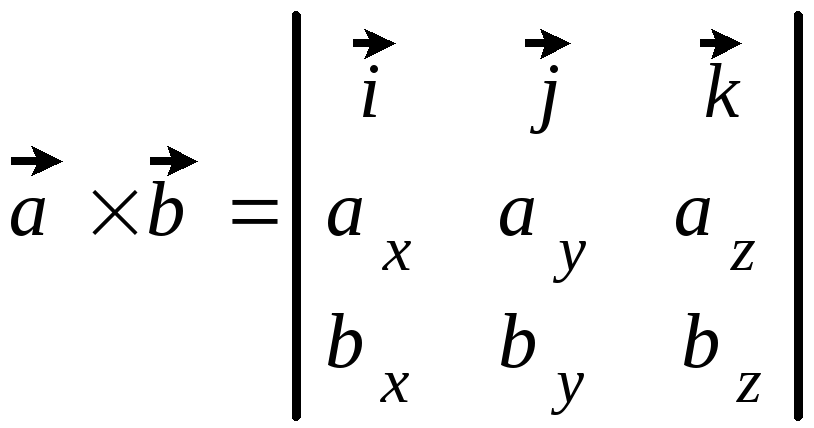 . (2.12)
. (2.12)

![]() .
Геометричний зміст векторного добутку.
.
Геометричний зміст векторного добутку.
М
![]() векторного добутку дорівнює площі
паралелограма, побудова-ного на векторах
векторного добутку дорівнює площі
паралелограма, побудова-ного на векторах
![]() і
і
![]() ,
віднесених до спільного початку, тобто
,
віднесених до спільного початку, тобто
![]() .
(2.13)
.
(2.13)

![]() .
Фізичні додатки.
.
Фізичні додатки.
-
Момент сили
 ,
прикладеної до
,
прикладеної до
точки
![]() відносно точки О, дорівнює
відносно точки О, дорівнює
векторному добутку сили
![]() на
на
вектор
![]() :
:
![]() .
.
2. Швидкість
![]() точки
точки
![]() твердого тіла, яке
обертається з кутовою швидкістю
твердого тіла, яке
обертається з кутовою швидкістю
![]() навколо нерухомої осі
навколо нерухомої осі
![]() ,
визначається формулою Ейлера
,
визначається формулою Ейлера
![]() .
.
3. Якщо електрон, з
зарядом
![]() рухається зі швидкістю
рухається зі швидкістю
![]() в магнітно-му полі постійної напруженості
в магнітно-му полі постійної напруженості
![]() ,
то на електрон діє сила
,
то на електрон діє сила
![]() Лоренца
Лоренца
 .
.
4. Площа
![]() ,
дорівнює половині площі паралелограма
,
дорівнює половині площі паралелограма
 . (2.14)
. (2.14)
2.3.1. Розв’язок типового прикладу завдання 3 ргр
Обчислити площу паралелограма,
побудованого на векторах
![]() і
і
![]() ,
якщо:
,
якщо:
а)
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
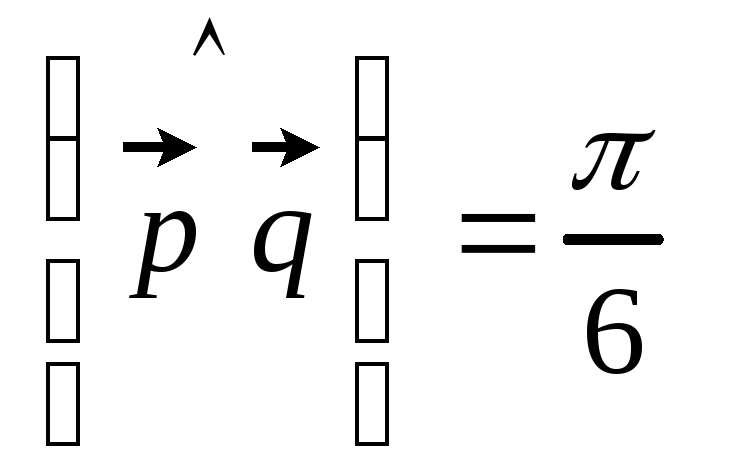 ;
;
б)
![]() ;
;
![]() .
.
Розв’язок. Площа паралелограма,
побудованого на векторах
![]() і
і
![]() ,
згідно формули (2.26) дорівнює модулю їх
векторного добутку
,
згідно формули (2.26) дорівнює модулю їх
векторного добутку
![]() .
.
Знайдемо векторний добуток векторів
![]() і
і
![]()
а)
![]()
![]()
![]() .
.
Тоді площа паралелограма
![]()

 (кв.
од.).
(кв.
од.).
Відповідь: 7 кв. од.
б) Якщо вектори задані своїми проекціями на осі координат, то в цьому випадку їх векторний добуток обчислюється за формулою (2.25)

![]() .
.
Тоді площа паралелограма
![]() (кв. од.)
(кв. од.)
Відповідь:
![]() кв. од.
кв. од.
2.4. Мішаний добуток трьох векторів
![]() .
Мішаним добутком трьох
векторів
.
Мішаним добутком трьох
векторів
![]() ,
,
![]() і
і
![]() називається число, яке дорівнює добутку
вектора
називається число, яке дорівнює добутку
вектора
![]() скалярно на вектор
скалярно на вектор
![]() :
:
![]() ,
або
,
або
![]() . (2.15)
. (2.15)
Якщо вектори задано своїми координатами, то мішаний добуток трьох векторів дорівнює визначнику третього порядку, який складається з відповідних координат векторів, що перемножуються
![]()
 . (2.16)
. (2.16)
![]() .
Властивості мішаного добутку
.
Властивості мішаного добутку
1. Якщо в мішаному добутку поміняти місцями довільні два множника, то мішаний добуток змінить знак на протилежний
![]() .
.
2. При циклічній перестановці множників мішаний добуток не змінюється:
![]()
![]() .
.
3. Вектори
![]() ,
,
![]() ,
,
![]() компланарні тоді і тільки тоді,
коли їх мішаний добуток дорівнює нулю.
компланарні тоді і тільки тоді,
коли їх мішаний добуток дорівнює нулю.
![]() .
Геометричний зміст мішаного добутку
.
Геометричний зміст мішаного добутку
М одуль
мішаного добутку
одуль
мішаного добутку
![]()
дорівнює об’єму паралелепіпеда,
побудованого на векторах
![]() ,
,
![]() і
і
![]()
віднесених до спільного початку:
![]() .
(2.17)
.
(2.17)
![]() .
Додаток
.
Додаток
Об’єм трикутної піраміди
(тетраедра), побудованої на векторах
Рис. 2.13![]() ,
,
![]() ,
,
![]() дорівнює
дорівнює
![]() .
(2.18)
.
(2.18)
