1.4. Розв’язок типового прикладу|зразків| завдання|задавання| 1 ргр

Розв’язати|розв'язання||рішати||рішати| систему алгебраїчних рівнянь

а) за формулами Крамера, б) матричним способом, в) методом Гауса.

Розв’язок.

а) Розв’яжемо систему за формулами Крамера, які мають вигляд:

, , ,

де – визначник системи рівнянь; , , – визначники невідомих, отримані|одержувати| із|із| заміною його першого, другого і третього стовпця відповідно стовпцем вільних членів.

Запишемо визначники , , , і обчислимо|обчислятимемо| їх:

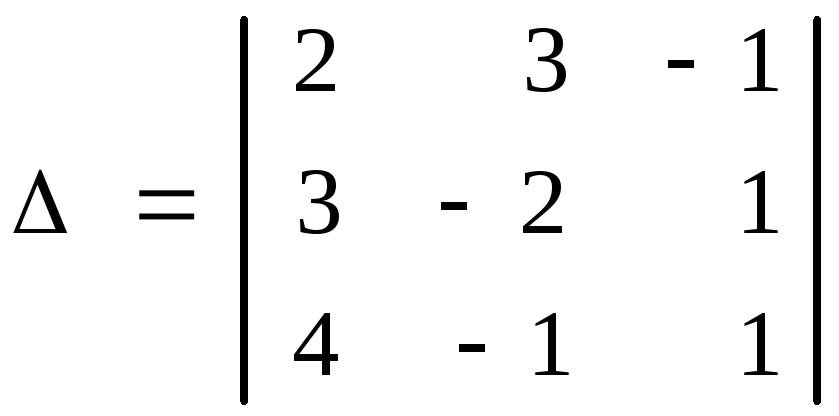
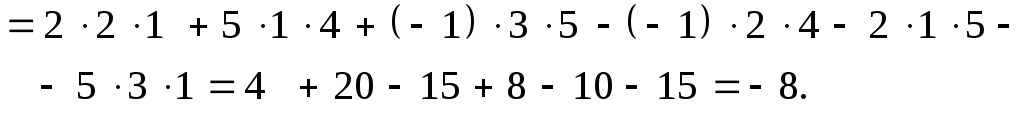
Тепер знайдемо невідомі , , за формулами (1.6)

; ; .

Відповідь: ; ; .

б) Розв’яжемо систему рівнянь матричним способом.

Позначимо через матрицю заданої|вихідної| системи рівнянь, через – матрицю-стовпець невідомих і через – матрицю-стовпець вільних членів:

, ,

Якщо система лінійних рівнянь в матричному вигляді|виді| записується|занотовує|, , то матриця невідомих знаходиться|перебуває| із|із| рівняння .

Для знаходження матриці невідомих , знайдемо обернену матрицю (див. розділ 1.2) і помножимо її на матрицю-стовпець вільних членів.

Оскільки|тому що| матриця невироджена (як було визначено раніше, ( ), то для неї існує обернена матриця .

Обернену матрицю знайдемо в наступній|слідуючій| послідовності:

1) Запишемо транспоновану матрицю – матрицю , в якій рядки матриці замінені її стовпцями з|із| тими ж номерами:

.

Обернену матрицю можна отримати|одержувати| за формулою:

,

де – визначник матриці ,

– алгебраїчні доповнення, які дорівнюють визначникам, що отримані викреслюванням -го рядка і -го стовпця транспонованої матриці, взяті із|із| знаком .

Знайдемо алгебраїчні доповнення транспонованої матриці :

; ; ;

; ; ;

; ; .

Таким чином ,

а розв’язок системи рівнянь визначається співвідношенням

.

Знайдемо значення , , :

= ;

= ;

= .

Підставляючи замість , , числові значення, отримаємо:

.

Відповідь: ; ; .

в) Розв’яжемо систему рівнянь методом Гауса.

Запишемо розширену матрицю системи

і зробимо елементарні перетворення, щоб привести її до трикутного вигляду.

Зробимо коефіцієнт рівним одиниці і обнулимо коефіцієнти , і .|

Для цього:

а) поміняємо місцями перший і другий рядки, а потім віднімемо із першого рядка другий. Результат запишемо замість першого рядка:

~

~

б) віднімемо від другого рядка перший, помножений на 2. Результат запишемо замість другого рядка:

~

~

в) віднімемо від третього рядка перший, помножений на 4. Результат запишемо замість третього рядка:

~

~

г) помножимо другий рядок на 19, а третій на 13. Потім віднімемо від отриманого третього рядка другий і результат запишемо замість третього рядка:

~

.

Здійснимо зворотний хід методу Гауса, відновивши рівносильну| систему за перетвореною розширеною матрицею:

З|із| останнього рівняння маємо .

Підставляємо значення в друге рівняння і знаходимо|находимо| :

.

Підставляючи значення і в перше рівняння, знаходимо|находимо| :

.

Відповідь: ; ; .