Деякі типи кривих на площині, заданих

в полярних координатах:

Коло ;

Кардіоїда ;

Спіраль Архімеда ;

Чотирьохпелюсткова роза ;

Лемніската Бернуллі ;

параметрично:

Коло , , ;

Еліпс , , ;

Астроїда ; , ;

Циклоїда ; , .

4. Аналитическая геометрия в пространстве

4.1. Плоскость

4. Аналітична геометрія в просторі

4.1. Площина . Основні рівняння площини

1. Загальне рівняння площини

, (4.1)

де вектор, перпендику-

лярний площині (рис. 4.1).

2. Нормальне рівняння площини

, (4.2)

де довжина перпендикуляра, прове-

деного до площини з початку координат;

кути, які цей перпендикуляр

утворює з додатними напрямами корди-

натних осей , відповідно (рис.4.2).

Для приведення загального рівнян-

ня площини (4.1) до нормального виду,

потрібно помножити його на нормую-

чий множник

, (4.3)

при цьому знак нормуючого множника

повинен бути протилежним знаку в рівнянні (4.1). Якщо , то знак може бути довільним.

2. Рівняння площини в відрізках на осях

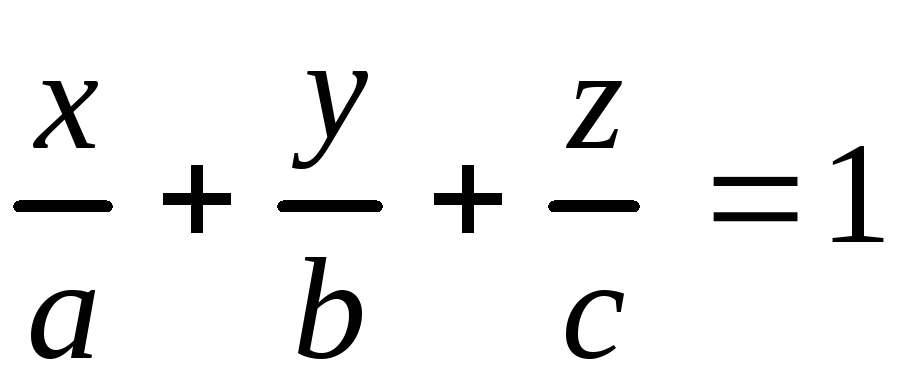, (4.4)

де відрізки, які відтинає площина на координатних осях .

3. Де відрізки, які відтинає площина на координатних осях

. (4.5)

4. Рівняння площини, яка проходить через три точки , ,

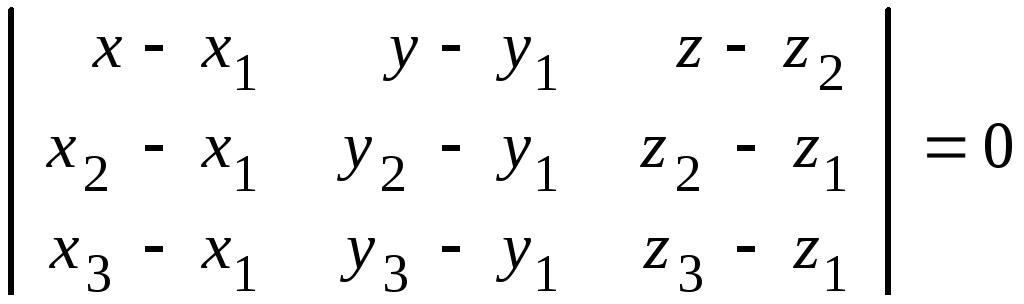. (4.6)

. Основні задачі на площину

1. Кут між двома площинами і дорівнює куту між їх векторами нормалі , :

. (4.7)

Знак « + » відповідає вибору гострого кута, знак « – » – тупого кута.

2. Напрямні косинуси нормалі визначаються по формулам

; ;

. (4.8)

Знак кореня береться протилежним знаку вільного члена рівняння (4.1). Якщо , то знак довільний.

3. Умова паралельності площин

. (4.9)

4. Умова перпендикулярності площин

. (4.10)

. Відстань від точки до площини

. (4.11)

4.1.1. Розв’язок типового прикладу завдання 8 ргр

Задано координати точок , , , . Потрібно:

1. Написати рівняння площини: а) – що проходить через точку перпендикулярно вектору ; б) – що проходить через точку пара-лельно векторам і ; в) – що проходить через точки .

2. Перевірити, чи виконується умова перпендикулярності|перпендикуляра| площин , |площини|, і паралельності площин|площини| , .

3. Знайти відстань від точки до площини .

Розв’язок. 1. а) Рівняння площини , яка проходить через точку перпендикулярно вектору має вигляд (4.6):

. (1)

За |спрямовувати|вектор нормалі приймемо вектор .

Замінивши в рівнянні пучка площин|площини| (1) коефіцієнти , , числами 4, , , і підставивши замість , , координати точки , отримаємо рівняння площини :

; .

б) Координати вектора , перпендикулярного векторам і знайдемо з обчислення їх векторного добутку.

Визначимо координати вектора :

Тоді:

Напишемо рівняння площини :

.

в) Рівняння площини, яка проходить через точки , , , має вигляд (4.7):

. (3)

Підставивши в (3) координати точок , , , отримаємо:

.

Розкладемо визначник за елементами першого рядка:

. .

2. Запишемо умову перпендикулярності площин і :

– виконується.

Умова паралельності площин і

– виконується.

3. Відстань від точки до площини , заданої рівнянням , знайдемо за формулою (4.13):

. (4)

Підставляючи в рівняння (4) знайдені значення коефіцієнтів , , , і координати точки маємо:

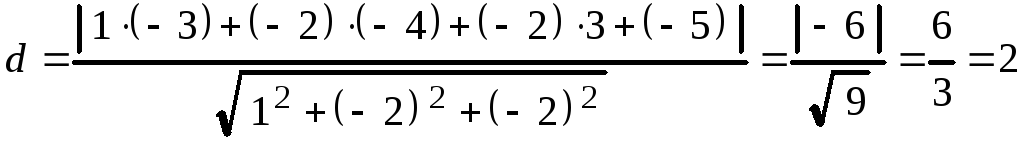(од. довжини.)

Відповідь: 1. а) ; б) ; в) ; 2. Виконується 3. од. довжини.