Лабораторные работы по механике

Лабораторная работа №7

ИЗМЕРЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ С ПОМОЩЬЮ ТРИФИЛЯРНОГО ПОДВЕСА

ЦЕЛЬ РАБОТЫ

Измерение и использование метода крутильных колебаний на трифилярном подвесе для измерения моментов инерции твердых тел. Проверка теоремы Штейнера.

ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Предварительно необходимо изучить теоретические основы работы №5.

Т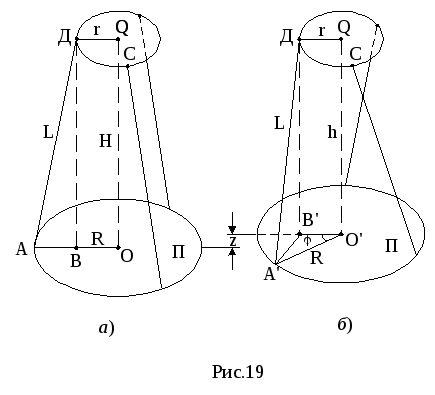 рифилярный подвес в положении равновесия показан на рис.19а. Платформа П подвешена на трех нитях, прикрепленных к платформе в вершинах равностороннего треугольника. Верхние концы нитей прикреплены к неподвижной шайбе С также в вершинах равностороннего треугольника. Треугольники вписаны в окружности, соответственно, радиусов R и r. Центры окружностей О и Q лежат на вертикальной оси. В положении равновесия расстояние между платформой П и шайбой С равно Н, а сила тяжести платформы П уравновешена силами натяжения трех нитей. При повороте платформы на угол j от положения равновесия ее нити подвеса перекручиваются и их силы натяжения создают момент сил, стремящийся повернуть платформу в положение равновесия, а сама платформа поднимается на высоту z (рис.19). В результате платформа П начинает совершать крутильные колебания.

При крутильных колебаниях платформы П ее отклонение от положения равновесия характеризует угол j. Если силами сопротивления движению можно пренебречь, то колебания становятся гармоническими:

, (1)

где j_m - амплитуда угла поворота; t - время колебаний;

Т - период колебаний; a₀ - начальная фаза.

Угловую скорость w платформы П найдем дифференцированием j по времени:

. (2)

Из формулы (2) следует, что амплитуда угловой скорости равна . (3)

При крутильных колебаниях платформы П происходит переход кинетической энергии вращательного движения платформы в потенциальную энергию подъема платформы относительно положения равновесия Е_Р = mgz и наоборот. Механическая энергия крутильных колебаний Е равна сумме кинетической и потенциальной энергий: Е = E_k + Е_р .

В момент прохождения платформы П через положение равновесия Е_Р = 0, а кинетическая энергия E_k максимальна и равна полной энергии. С учетом формулы (3) получим

. (4)

В момент отклонения платформы П на максимальный угол j_m она поднимается на максимальную высоту z_m от положения равновесия, а кинетическая энергия равна 0. Энергия колебаний Е равна максимальной потенциальной энергии:

. (5)

Обозначим длину нитей подвеса буквой L. Из DАДВ (рис.19а) следует , (6)

а из DА¢ДВ¢ и D А¢В¢О¢ (см.рис.19б) получим

. (7)

Вычитая уравнение (7) из уравнения (6), найдем

или

. (8)

При малых углах отклонения j, т.е. при выполнении условия z<<H, , , уравнение (8) принимает вид:

. (9)

Соответственно для максимальных высоты подъема z_m и угла отклонения j_m из уравнения (9) следует

. (10)

Тогда . (11)

Подставляя формулу (11) в формулу (5), получим энергию крутильных колебаний

. (12)

Приравнивая формулы (4) и (12), определяющие механическую энергию крутильных колебаний, получим уравнение

,

из которого найдем момент инерции платформы П относительно вертикальной оси OQ

, (13)

где t - время n полных колебаний платформы П.

Определяя момент инерции I по формуле (13), полуширину доверительного интервала DI (абсолютную погрешность) вычисляют с помощью формулы:

, (14)

т.е. DI = IE, где Е - относительная погрешность момента инерции I, а Dt, Dm, …, DH - абсолютные погрешности соответствующих величин.

При экспериментальном измерении момента инерции I_k тела с номером k сначала наблюдают колебания ненагруженной платформы П и по формулам (13) и (14) находят момент инерции пустой платформы I₀ и полуширину доверительного интервала DI₀. Далее испытуемое тело помещают в центр платформы П и повторяют измерения для платформы с телом, а с помощью формул (13) и (14) определяют момент инерции платформы с телом I_0k и полуширину доверительного интервала DI_0k. Тогда момент инерции одного тела равен

I_k = I_0k - I₀, к=1,2 , (15)

а полуширина доверительного интервала DI_k определяется формулой

. (16)