Механика, работа №6

Лабораторные работы по механике

Лабораторная работа № 6

ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ С ПОМОЩЬЮ КРУТИЛЬНЫХ КОЛЕБАНИЙ

ЦЕЛЬ РАБОТЫ

Экспериментальное измерение моментов инерции твердых тел с помощью крутильных колебаний.

ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

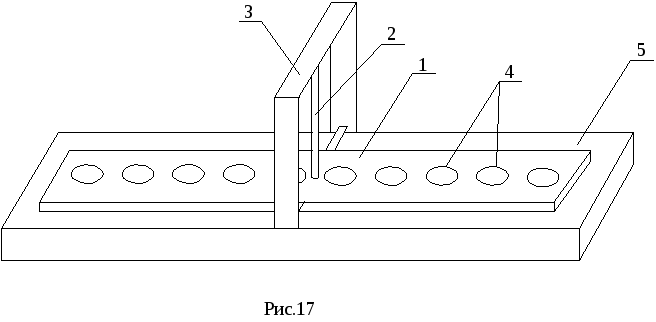
Предварительно необходимо изучить теоретические основы работы №5. Экспериментальная установка (рис.17), называемая крутильным маятником, представляет собой платформу 1, подвешенную на тонком упругом стальном стержне 2 к горизонтальной раме 3. Платформа может совершать крутильные колебания относительно вертикальной оси, проходящей вдоль тонкого стержня 2. На платформе для крепления испытуемых тел имеется 8 пар отверстий 4, расположенных симметрично относительно оси вращения. Номера отверстий увеличиваются по мере удаления от оси вращения. В таблице 1 показаны расстояния отверстий до оси. Испытуемые тела имеют штыри, которые вставляются в отверстия. Таким образом тела закрепляются на платформе. Экспериментальная установка располагается на массивном основании 5.

Таблица 1

Номер отверстия	1	2	3	4	5	6	7	8
Расстояние d от оси вращения до центра отверстия, см	2	3	4	5	6	7	8	9

При повороте платформы 1 на угол  относительно вертикальной оси происходит закручивание стального стержня 2 на этот угол. В стержне возникают упругие силы, момент которых

действует на платформу. Коэффициент k называется коэффициентом упругости. Уравнение динамики вращательного движения

пустой платформы с моментом инерции I₀ относительно вертикальной оси принимает вид:

или . (1)

Уравнение (1) является уравнением гармонических колебаний с круговой частотой и периодом колебаний .

Итак, пустая платформа совершает гармонические крутильные колебания с периодом

(2)

Располагая на платформе на одинаковых расстояниях d_i от оси вращения два одинаковых грузика с массами m, получают момент инерции системы

,

где момент инерции I_i одного грузика определяется теоремой Штейнера (см. лаб. работу № 5):

. (3)

В формуле (3) I_с - момент инерции грузика относительно вертикальной оси, проходящей через центр масс грузика. Тогда период крутильных колебаний равен

. (4)

Помещая эти же грузики на другом расстоянии d_j от оси вращения, получим формулы

,

где . (5)

В этом случае период колебаний T_j равен

. (6)

Возводя в квадрат формулы (2), (4), (6), получим систему уравнений:

, (7)

, (8)

. (9)

Вычитая уравнение (8) из уравнения (9), найдем уравнение

. (10)

Подставляя в уравнение (10) формулы (3) и (5), получим коэффициент упругости

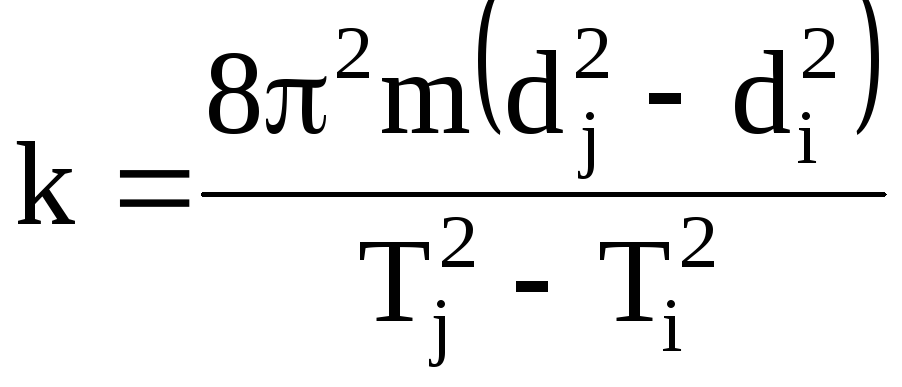. (11)

Подставляя формулу (11) в уравнение (7), найдем момент инерции I₀ пустой платформы:

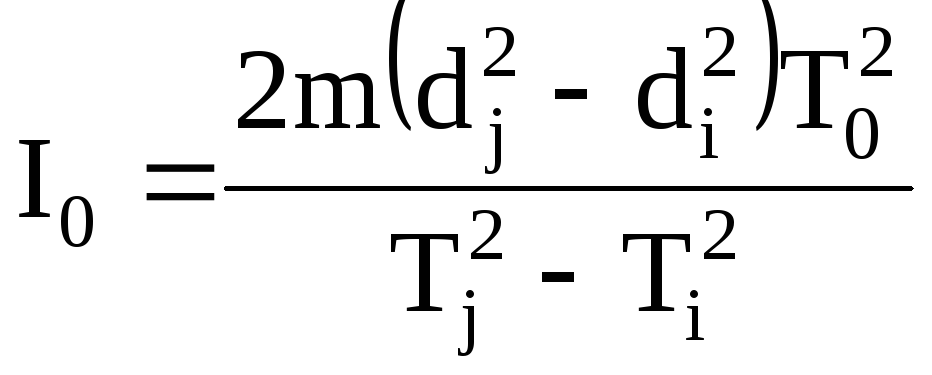, (12)

Вычитая уравнение (7) из уравнения (8) и подставляя в результат формулу (11), получим момент инерции I_i грузика, центр масс которого находится на расстоянии d_i от вертикальной оси:

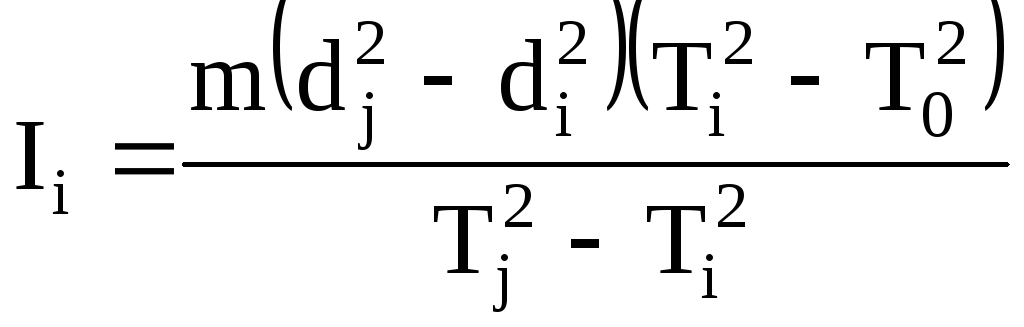. (13)

Период Т или время одного полного колебания экспериментально определяют, измеряя время t для n полных колебаний:

. (14)

Подставляя формулу (14) в формулы (12) и (13), найдем расчетные формулы для определения момента инерции I₀ пустой платформы

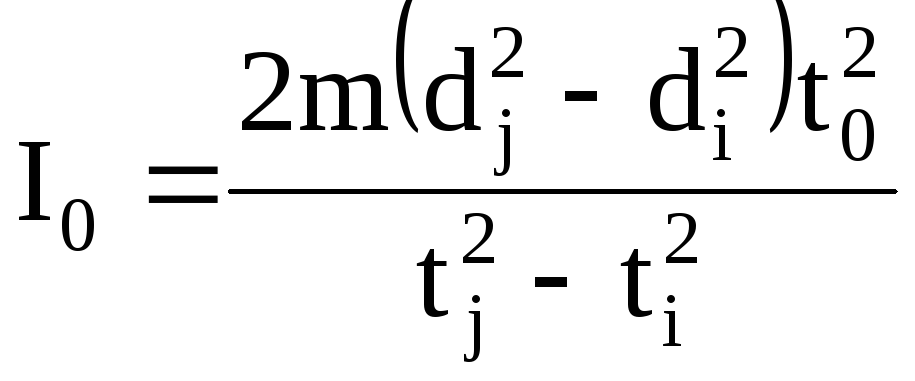. (15)

и момента инерции I_i грузика

. (16)

Сравнивая формулы (15) и (16) можно величину I_i выразить через момент инерции I₀ пустой платформы:

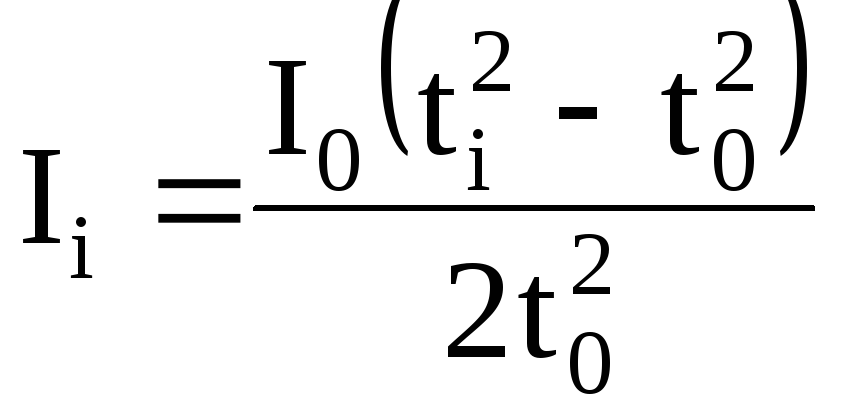. (17)

При вычислении момента инерции I₀ пустой платформы по формуле (15) полуширину доверительного интервала I₀ находят с помощью формулы:

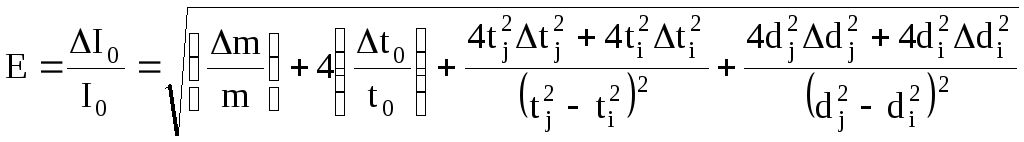. (18)

Анализ формулы (18) показывает, что относительная погрешность уменьшается с увеличением величины . Поэтому для уменьшения погрешности измерения целесообразно величину выбирать минимальной (i = 1 или i = 2), а величину максимальной (j = 7 или j = 8).

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Упражнение 1. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ПЛАТФОРМЫ

1. Измерьте время t₀ десяти (n = 10) полных колебаний пустой платформы, наблюдая величину t₀ не менее 5 раз. Результаты наблюдений занесите в таблицу 2.

2. Поместите на платформу на минимальных расстояниях d_i от оси вращения (i = 1 или i = 2) два одинаковых грузика и измерьте время t_i. Наблюдайте величину t_i не менее 5 раз. Результаты наблюдений запишите в таблицу 2.

3. Расположите грузики на платформе на максимальных расстояниях от оси вращения (j = 8 или j = 7) и измерьте время t_j десяти полных колебаний платформы с грузиками. Наблюдайте величину не менее 5 раз. Результаты наблюдений запишите в таблицу 2.

4. Найдите средние значения величин , , , их выборочные оценки средних квадратичных отклонений S(t) и полуширину доверительных интервалов t. Результаты вычислений запишите в таблицу 2.

5. Подставляя средние значения в формулу (15), определите момент инерции I₀ пустой платформы. Учитывая, что см, по формуле (24) найдите относительную погрешность результата измерения. Полуширину доверительного интервала I₀ определите по формуле:

.

Запишите результат измерения в виде доверительного интервала: .

Таблица 2

Результаты наблюдений	Номер наблюдения
	1 2 3 4 5
Среднее значение t
Полуширина доверительного интервала t

Упражнение 2. ИЗМЕРЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ

6. Располагая на платформе два одинаковых тела (грузика) на равных расстояниях d_i (i = 1, 2, 3, … , n) от оси вращения, измерьте время t_i десяти полных колебаний нагруженной платформы для всех возможных расстояний d_i. Результаты измерений запишите в таблицу 3 (n - максимальный номер отверстия).

Таблица 3

Номер отверстия	1	2	…	n
Расстояние до оси di
Время 10 колебаний ti
Момент инерции Ii

7. Используя найденные в упражнении №1 численные значения времени 10 полных колебаний t₀ и момента инерции I₀ пустой платформы, по формуле (17) найдите моменты инерции I_i одного тела на разных расстояниях d_i от оси вращения. Результаты вычислений I_i запишите в таблицу 2.

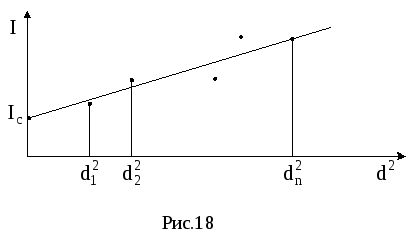
8. Откладывая по осям координат и I_i , постройте на диаграмме (рис.18) экспериментальные точки. В соответствии с теоремой Штейнера

экспериментальные точки должны лежать на одной прямой, которая пересекает ось координат в точке I_с. I_с - момент инерции тела относительно вертикальной оси, проходящей через центр масс тела.

9. Определите с помощью графика, показанного на рис.18, величину I_с и полуширину доверительного интервала I_с. Для этого через экспериментальные точки нужно провести прямую и найти точку пересечения этой прямой и оси координат. Применяя при проведении прямой метод наименьших квадратов [8], получим расчетные формулы для I_с и выборочной оценки среднего квадратичного отклонения S(I_с):

,

,

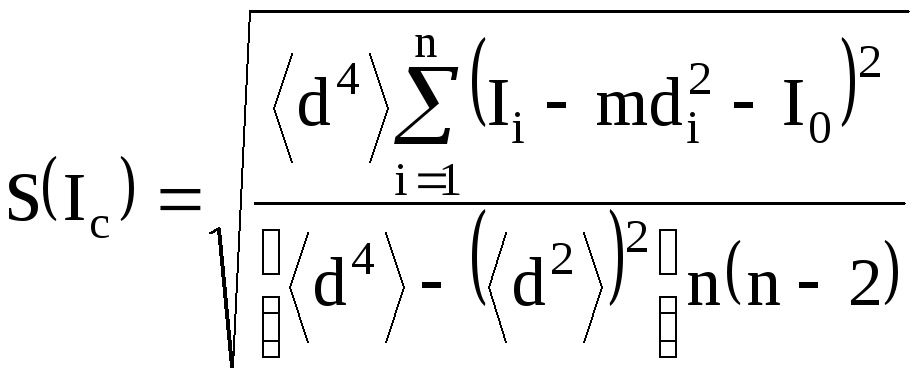где , , .

Запишите результат измерения в виде доверительного интервала: .

10. Повторите пункты 6 - 9 для другой пары тел.

11. Измерьте размеры изучаемых тел и по формулам (4) и (5) лаб. работы 5 теоретически найдите моменты инерции I_с этих тел. Сравните теоретические результаты с экспериментальными.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Укажите цель данной лабораторной работы.

2. Мерой какой величины является момент инерции тела относительно оси ?

3. По какой формуле можно вычислить момент инерции относительно оси системы материальных точек ?

4. Как вычислить момент инерции произвольного тела относительно оси?

5. Сравните моменты инерции трех тел одинаковой формы и размеров, если одно тело изготовлено из алюминия, другое - из железа, а третье - из свинца.

6. На каком расстоянии от оси находится материальная точка массой m = 10 г, если ее момент инерции относительно этой оси равен I = 410^-4 кг-м² ?

7. Моменты инерции относительно оси О₁О₂ трех тел по отдельности равны I₁ = 5 кгм²; I₂ = 3 кгм²; I₃ = 2 кгм². Найдите момент инерции системы указанных тел относительно той же оси О₁О₂ .

8. Какой радиус основания имеет прямой круглый однородный цилиндр массой m = 6,25 кг, если момент инерции цилиндра относительно оси, проходящей через его центр масс параллельно боковой поверхности, равен I =0,125 кгм² ?

9. Какую массу имеет прямой круглый однородный цилиндр высотой Н = 10 см и радиусом основания R = 5 см, если момент инерции цилиндра относительно оси, проходящей через его центр масс перпендикулярно боковой поверхности, равен I = 0,01 кгм² ?

10. Сформулируйте теорему Штейнера.

11. Как найти момент инерции тела относительно оси, не проходящей через центр масс тела ?

12. Как момент инерции однородного шара относительно оси зависит от расстояния центра шара до этой оси ?

13. Два шара, изготовленные из одного металла, имеют одинаковую массу. Сравните моменты инерции шаров относительно оси, проходящей через их центры, если один из шаров имеет внутри полость.

14. Сравните моменты инерции двух однородных шаров одинаковой массы относительно оси, проходящей через центры шаров, если плотность шаров: 1) одинакова; 2) различается в 2 раза.

15. Нарисуйте эскиз экспериментальной установки.

16. Где помещают изучаемые тела ?

17. Какая часть экспериментальной установки совершает крутильные колебания ?

18. Для чего в платформе сделаны отверстия ?

19. Как найти расстояние от грузика до оси вращения ?

20. Как изменится период крутильных колебаний платформы, если ее момент инерции увеличится в 4 раза ?

21. Как период крутильных колебаний платформы зависит от коэффициента упругости стержня, на котором она подвешена ?

22. Выведите расчетную формулу для определения момента инерции I₀ пустой платформы.

23. Какая величина определяется в упражнении 1?

24. Какие измерения проводятся при выполнении упражнения 1 ?

25. Как находят полуширину доверительного интервала при определении момента инерции пустой платформы ?

26. Какой должна быть величина 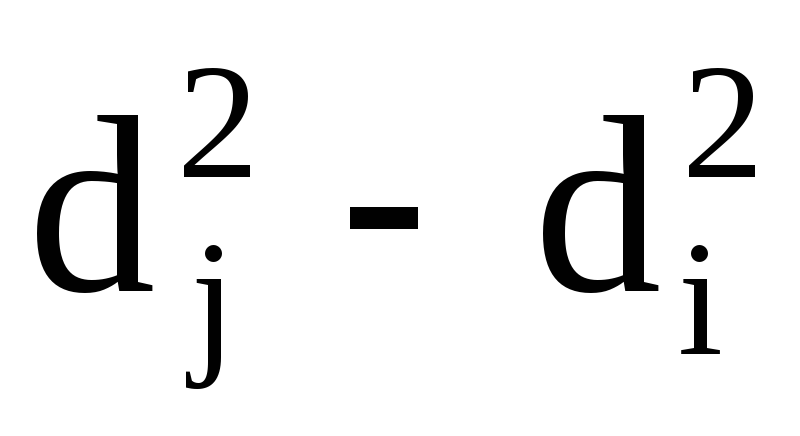, чтобы относительная погрешность результата измерения в упражнении 1 была минимальной ?

27. Изменится ли период колебаний и момент инерции платформы, если платформу подвесить не на стальной стержень, а на медный ?

28. Что измеряют в упражнении 2 ?

29. Укажите расчетную формулу для определения момента инерции грузика, центр масс которого находится на расстоянии d_i от оси вращения крутильных колебаний.

30. Какова последовательность действий при выполнении упражнения №2 ?

7

©МАТИ, 2003