4.6. Временные диаграммы
Для того чтобы полнее представить себе работу схемы счетчика, необходимо рассмотреть его временную диаграмму. На рис. 4.10 приведен пример возможной последовательности событий, происходящих в нашей схеме. Предполагается, что переходы между состояниями (изменения значений триггеров) происходят на отрицательном фронте тактирующего сигнала и что начальным состоянием счетчика является S0. Вначале х = 0. Поэтому в момент времени t0 счетчик переходит в состояние S1, затем, в момент времени t1 он переходит в состояние S2 (и на выходе z является значение 1), а затем, в момент времени t2, — в состояние S3 (на и выходе z мы снова видим 0). Далее, в момент времени t3, счетчик снова переходит состояние S0. Предположим, что в этот момент входное значение х меняется на 1, чего счетчик начинает считать в обратном порядке. Когда в момент времени t5 счетчик снова достигнет состояния S2, на выходе z опять появится значение 1
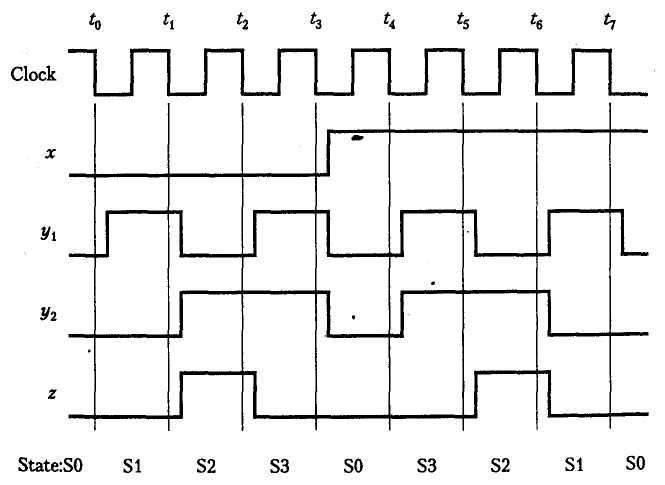
Рис. 4.10. Временная диаграмма для схемы, приведенной на рис. 4.9
Обратите внимание, что все изменения сигналов происходят сразу после появления отрицательного фронта тактового сигнала, и сигналы больше не меняются до тех пор, пока не появится отрицательный фронт следующего тактового сигнала.
Время задержки между фронтом тактового сигнала и изменением переменной уi- это время задержки на распространение сигнала в триггерах, на основе которых создана схема счетчика. Важно отметить, что вход х управляется тем же тактовым алом и изменяется в начале такта. Схемы, в которых все изменения управляются тактовым сигналом, называются синхронными последовательными схемами.
Еще одно важное наблюдение касается соответствия диаграммы состояний, представленной на рис. 4.8, временной диаграмме. Возьмем, к примеру, тактовый период между моментами времени t1 и t2. В течение этого времени схема находится в состоянии S2 и на ее входе сохраняется значение х = 0. На диаграмме состояний эта ситуация представлена исходящей из узла S2 стрелкой с надписью х = 0. Поскольку эта стрелка указывает на узел S3, на следующем фронте тактового сигнала (t2) переменные у1 и у2 принимают значения, соответствующие состоянию S3. А пока счетчик будет оставаться в состоянии S2, на выходе z будет значение 1.
4.7. Модель конечного автомата
Рассмотренный нами пример счетчика с прямым/обратным счетом, реализованного в виде синхронной последовательной схемы на основе триггеров и вентильной комбинаторной логики (рис. 4.9), легко обобщить до формальной модели конечного автомата, показанной на рис. 4.11.
В этой модели запаздывание при прохождении сигнала через элементы задержки равно длительности такта. Это время между изменениями, происходящими в точках Yi и соответствующими изменениями в точках уi. В данной модели предполагается, что через блок комбинаторной логики сигналы проходят без задержки; поэтому выходные значения z, Y1 и У2 являются мгновенными функциями входных значений х, у1 и у2
Рис. 4.11. Модель конечного автомата
. В реальной схеме все элементы, как показано на рис. 4.10, служат источниками определенных задержек. Схема будет работать правильно лишь при условии, что задержка блока комбинаторной логики не велика по сравнению с длительностью такта. Значения на выходах следующего состояния, Y1 и Y2, должны быть установлены таким образом, чтобы состояния триггеров изменились до окончания такта. Кроме того, в течение некоторого времени на выходе z требуемого значения может не быть, но оно должно появиться задолго до окончания такта.
Входы блока комбинаторной логики соединены с выходами триггеров уi предшествующих текущее состояние, и с внешним входом х. Выходы блока, обозначенные как Yi , соединены со входами триггеров и внешним выходом z. На отрицательном фронте тактового сигнала, соответствующем концу текущего такта, в триггеры загружаются значения выходов Yi которые становятся следующими значениями переменных состояния уi . Поскольку выходы триггеров соединены со входами блока комбинаторной логики, они вместе со следующим значением внешнего входа х определяют новые значения переменных z и Yi . На следующем такте значения Yi передаются на входы yi и процесс повторяется сначала. Таким образом, триггеры образуют обратную связь между выходом и входом комбинаторного блока с задержкой в один такт.
Хотя в рассмотренной нами схеме (рис. 4.11) имелся лишь один внешний вход и две переменные состояния, совершенно очевидно, что в схеме может быть нескольку переменных каждого из трех типов.