
- •Методы проецирования
- •Центральное проецирование
- •Взаимное положение прямых
- •Теорема о частном случае проецирования прямого угла
- •Плоскость
- •Следы плоскости
- •Плоскости общего положения (выше) Плоскости частного положения
- •Проецирующие плоскости
- •Теорема о принадлежности точки плоскости
- •Главные линии в плоскости
- •Линия наибольшего ската и линия наибольшего наклона плоскости
- •Взаимное положение прямых и плоскостей
- •Способы преобразования чертежа
- •Способ замены плоскостей проекции
- •Способ вращения
- •Поверхности вращения
- •Поверхности вращения
- •Пересечение фигур
- •Пересечение линии с поверхностью
- •Касание фигур
- •Пересечение поверхностей
- •3 Условия, при которых применяется этот метод:
Методы проецирования
-
Центральное проецирование
S – центр проецирования
π – плоскость проекции

 S
А, В – точки в
пространстве
S
А, В – точки в
пространстве
A', B' – проекции точек А и В на
плоскость проекции π
A B



A'
B'
π

-
Параллельное проецирование – это частный случай центрального проецирования, когда центр проецирования отнесен в бесконечность.

 S∞
S – направление
проецирования
S∞
S – направление
проецирования
А, В – точки в пространстве


 S
S S А', В' –
проекции
точек
S
S S А', В' –
проекции
точек
π – плоскость проекции
A B



 A'
B'
A'
B'
-
Ортогональное проецирование (перпендикулярное) – частный случай параллельного проецирования, когда проецирующие прямые перпендикулярны плоскости проекции.



 S
S






 A
S
B
A
S
B
A' α B' α
Инвариантные свойства ортогонального проецирования
-
Проекция прямой есть прямая;
-
Если точка принадлежит прямой в пространстве, то проекция точки принадлежит проекции этой прямой;
-
Если прямые пересекаются, то пересекаются и их проекции и точки пересечения проекций прямых являются проекции точек пересечения прямых в пространстве;
-
Если прямые параллельны, то параллельны и их проекции.
-
Если плоская фигура параллельна плоскости проекции, то проекция этой фигуры на плоскость конгруэнтна самой фигуре.
Ортогональное проецирование на 2 и 3 плоскости проекции
А – точка в пространстве
 Z
π1
– горизонтальная
плоскость
Z
π1
– горизонтальная
плоскость
π2 – вертикальная (фронтальная)

 плоскость
проекции
плоскость
проекции
π2 А' – горизонтальная проекция т.А


 A''
А'' –
вертикальная (фронтальная)
A''
А'' –
вертикальная (фронтальная)
 II
YA
проекция т.А
II
YA
проекция т.А






 ZA
A | A,
π1|=ZA;
|A, π2|=YA
ZA
A | A,
π1|=ZA;
|A, π2|=YA
X
 I
I
III Ax ZA
IV A'
π1

Y
Эпюр





A''
ZA
AX
X YA
A'
Проекция на 3 плоскости
Z

 π3
–
профильная плоскость
π3
–
профильная плоскость


 π2
|A,
π3|=XA
π2
|A,
π3|=XA



 A''
A''

 ZX
XA
π3
ZX
XA
π3



 II
I A A'''
II
I A A'''


 X
AX
ZA
O
X
AX
ZA
O

 III
IV YA
III
IV YA
 A'
AY
V
A'
AY
V

 π1
π1
VII Y
Эпюр
 Z
Z
A'' YA A'''



ZA


 X
Y
X
Y
YA
A'
Y
Чтобы построить профильную проекцию точки по имеющимся фронтальной и горизонтальной проекциям, необходимо через фронтальную проекцию точки провести прямую, перпендикулярную оси Z и на ней отложить координату Y точки вправо от оси Z , если она положительна, и влево от оси Z, если она отрицательна.
Проецирование прямой
Эпюр прямой общего положения

 A''
A''
a''
 B''
B''
 X
X
 B'
B'
a'
A'
Прямые частного положения
Прямые уровня
Горизонтальная прямая уровня Фронтальная прямая уровня
 b''
|b|=|b'| |c|=|c''|
c''
b''
|b|=|b'| |c|=|c''|
c''
 π1
=(b^π2)
α=(c^π1)
π1
=(b^π2)
α=(c^π1)
α

 X
X
X
X
 β
β
 b'
b'
c'
Профильная прямая уровня




 c
|| π3
A'' Z A'''
c
|| π3
A'' Z A'''


 B''
B'''
B''
B'''
 X
Y
X
Y

 A'
A'
 B'
Y
B'
Y
Прямые проецирующие
Горизонтально проецирующая прямая Фронтально проецирующая прямая
m | π1 n | π2

 m''
| X
n''≡k''
m''
| X
n''≡k''
A''≡m''

 X
X
X
X
n'≡k'
m'≡A'
Профильно проецирующая прямая
 A''
Z
A''
Z

 a''
A'''≡a'''
a''
A'''≡a'''

 X
a'
Y
X
a'
Y
A'
Y
Определение действительной величины отрезков прямой общего положения и наклонных углов



 B
B




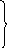
 ∆Z
A''0
B''
∆Z
A''0
B''
β ∆Z ZB




 α
α



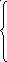
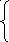
 A
ZB
A'' ZA
A
ZB
A'' ZA
X YB



 ZA
YA
∆Y B'
ZA
YA
∆Y B'
α


 B'
A'
B'0
B'
A'
B'0
 A0
α
∆Z
A0
α
∆Z
π1 A'0
Правило: чтобы определить действительную величину отрезка прямой общего положения, необходимо построить прямоугольный треугольник, у которого один катет – горизонтальная проекция отрезка. Второй катет по величине равен разности расстояний концов отрезка от плоскости отрезка π1, т.е. ∆Z. Гипотенуза этого треугольника равна действительной величине отрезка, угол между гипотенузой (действительной величиной отрезка) и катетом (горизонтальная величина отрезка) – α=([AB]^π1) угол наклона отрезка к горизонтальной плоскости отрезка π1.На основании фронтальной проекции отрезка действительная величина строится аналогично. β=([AB]^π2)
Теорема: Если точка в пространстве принадлежит прямой, то проекции точки принадлежат проекциям этой прямой.
Если точка делит отрезок в каком-то соотношении, то проекции точки делят проекции отрезка в том же соотношении.

 B''
M a => M' a' /\
M'
a''
B''
M a => M' a' /\
M'
a''
a'' [AM] [A''M''] [A'M']



 M''
[MB]
[M''B''] [M'B']
M''
[MB]
[M''B''] [M'B']
 A''
A''
 X
X

A' a'
M'
B'
Следы прямой
Следы прямой – точки пересечения прямой с плоскостями проекций.
 Ha
– горизонтальный след прямой
Ha
– горизонтальный след прямой


 Fa
– фронтальный след прямой
Fa
– фронтальный след прямой
π2

 Fa≡Fa''
Fa≡Fa''
II a''

 I
a
I
a



 Fa'
Fa'
Ha'' a'
 Ha≡Ha'
Ha≡Ha'
IV π1


 Эпюр
II
Эпюр
II
 I
Fa≡Fa''
I
Fa≡Fa''
 a''
a''
 IV
IV
Ha''

 X
X
a'
Ha≡Ha'
Правило: чтобы построить горизонтальный след прямой, необходимо продолжить фронтальную проекцию прямой до пересечения с осью X. Точка пересечения – это фронтальная проекция горизонтального следа прямой. Затем провести линию связи, перпендикулярную оси X из этой точки до пересечения с продолжением горизонтальной проекцией прямой. Получается точка – горизонтальный след прямой совпадает со своей горизонтальной проекцией. Фронтальный след прямой строится аналогично.
