Лекция №6
Многогранники
-
Классификация многогранников
Многогранной называется поверхность, образованная отсеками (частями) пересекающихся _ _ плоскостей _
Многогранник – з амкнутая многогранная поверхность. _
Элементы многогранников
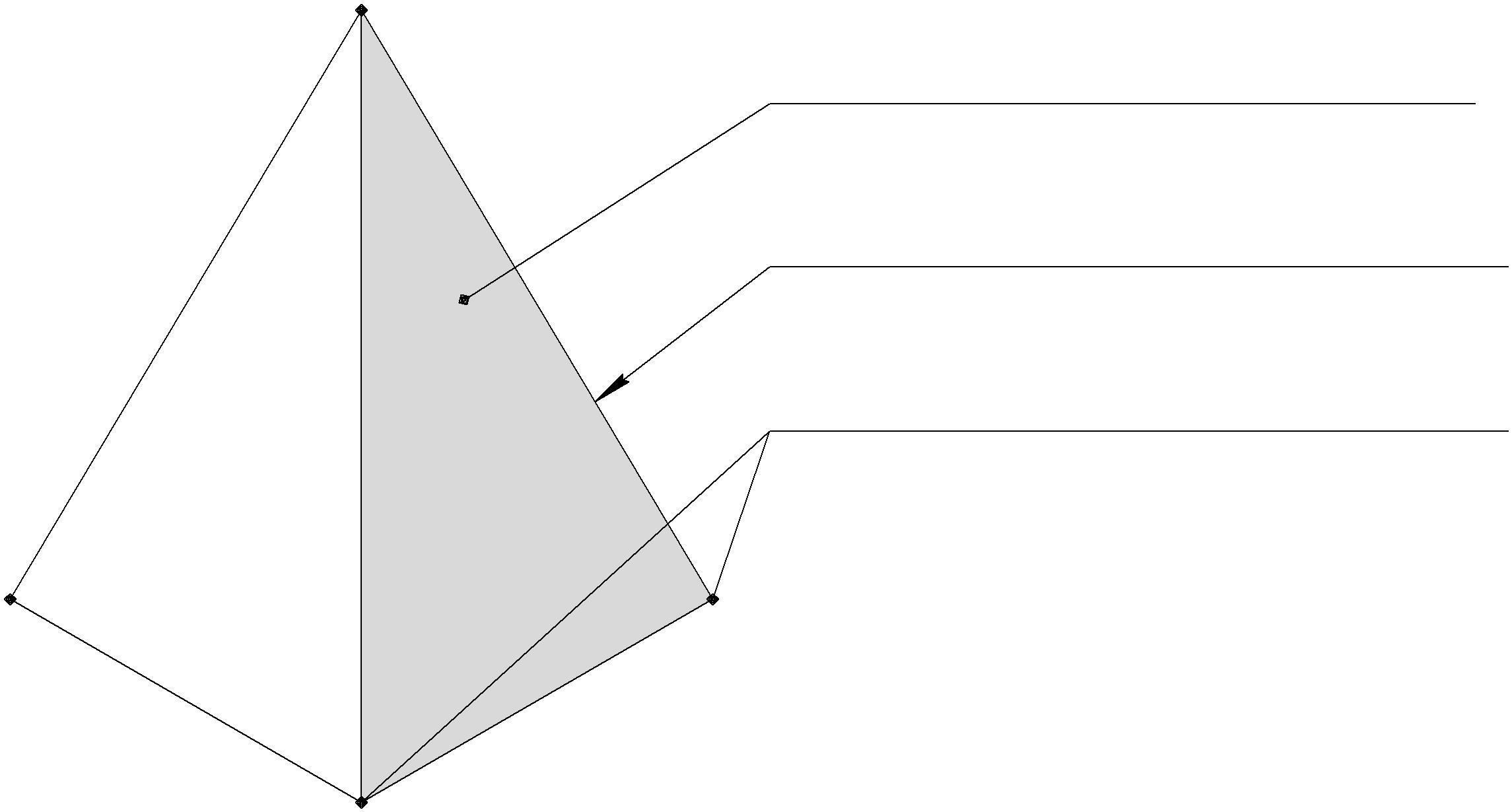
Классификация многогранников
-
Призмы - боковые рёбра параллельны между собой _
- прямые __ - наклонные ______ _
-
Пирамиды - все боковые рёбра пересекаются в одной точке _
Пирамида – всегда не проецирующий образ (общего положения). _
Правильные многогранники – многогранники, грани которых являются правильными________ ______ многоугольниками. (куб: грань – квадрат; тетраэдр: грань – правильный треугольник)_ __ ___ __ _________________ ____ _________________________________ _
-
Позиционные задачи. Пересечение многогранников плоскостью.
Сечение многогранника плоскостью – многоугольник. _
Стороны такого многоугольника – прямые пересечения граней многогранника с заданной плоскостью .
_
Вершины многоугольника – точки встречи рёбер с секущей плоскостью. _
Задачи I-го типа.
Оба ГО – частного положения – проецирующие. (имеют вырожденную проекцию _
Задача: Определить фигуру сечения призмы плоскостью. Найти н.в. фигуры сечения.
Дано:
α – фронтально проецирующая плоскость _
Призма – трёхгранная, грани – горизонтально проецирующие плоскости .
Решение:
Проекции результата есть на чертеже и лежат на вырожденных проекциях проецирующих образов _ (построения не требуются) __
В данном случае н.в. треугольника 123 находим способом плоско-параллельного перемещения. _
П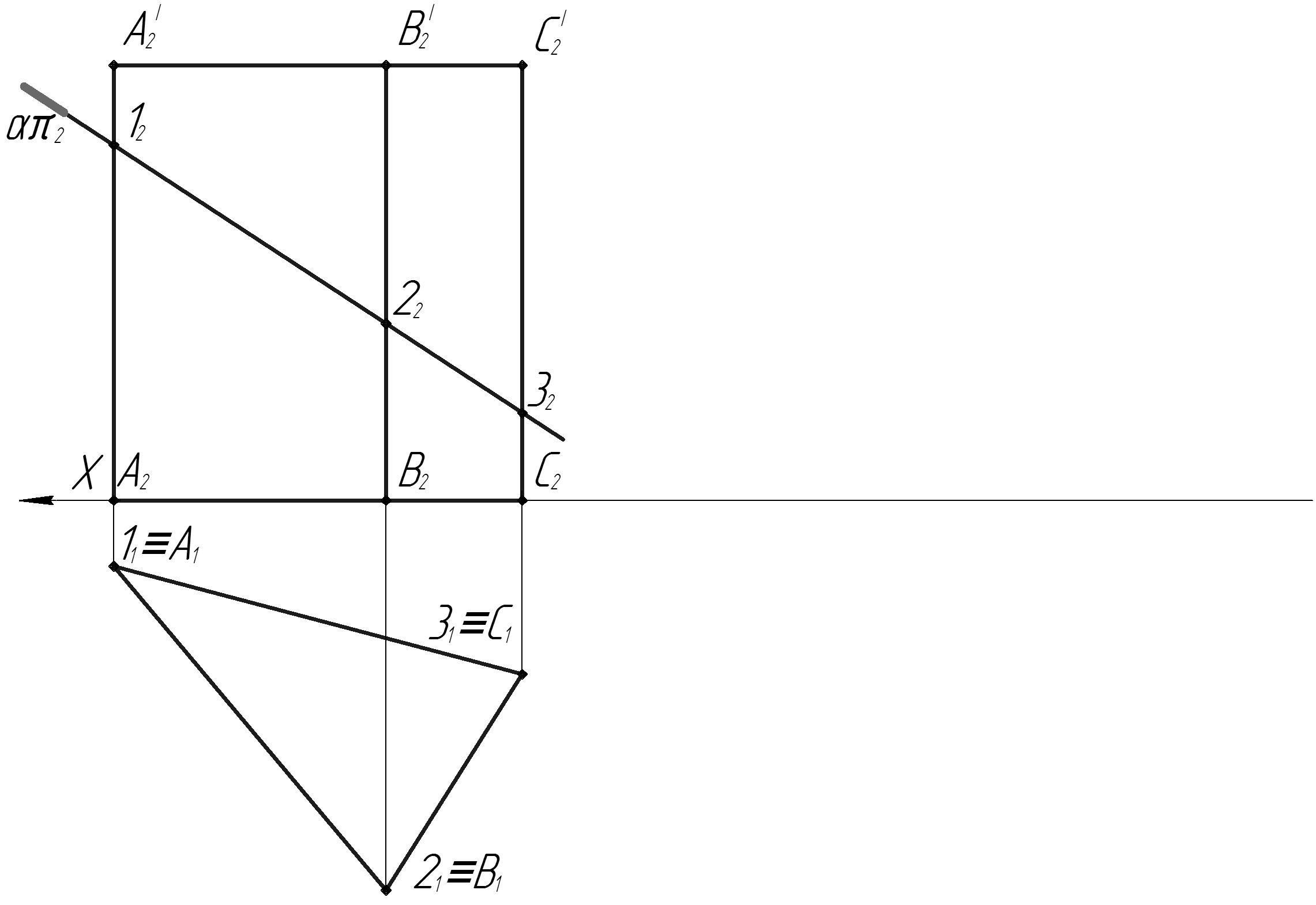
реобразовываем
проецирующую плоскость в плоскость
уровня.
_