Закон додавання швидкостей Галілея.
Принцип
відносності Галілея – рівняння механіки
Ньютона інваріантні відносно перетворень
Галілея, тобто вони залишаються незмінними
при переході від однієї інерціальної
системи до іншої. Або: ніякими механічними
дослідами, проведеними в середині
інерціальної системи відліку, неможливо
встановити – система перебуває в стані
спокою чи рхається рівномірно прямолінійно.
Закон додавання швидкостей Галілея -
Закон збереження імпульсу.
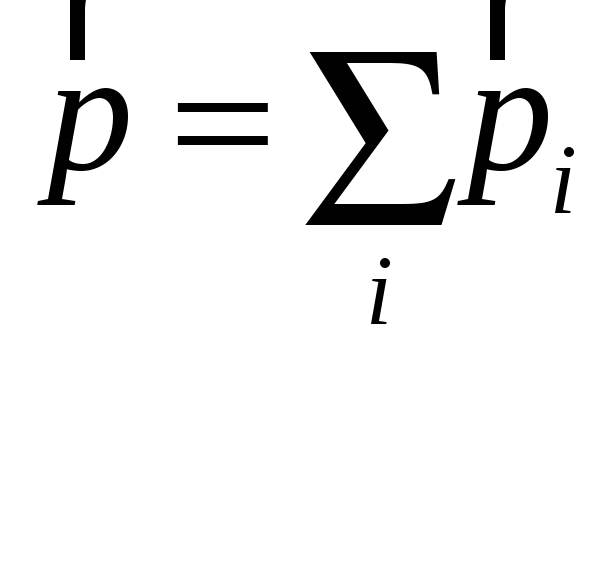
Під зовнішніми силами розуміють сили, які не входять в систему під внутрішніми – ті, що зумовлені взаємодією частинок системи.
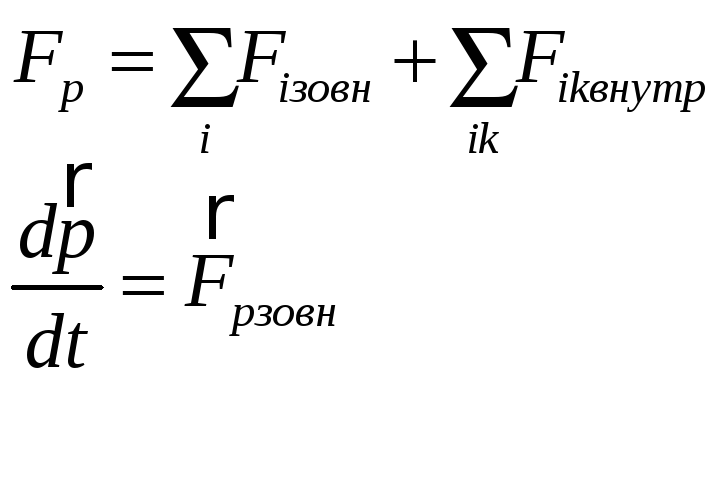
Якщо
,
то система вважається ізольованою,
звідси випливає
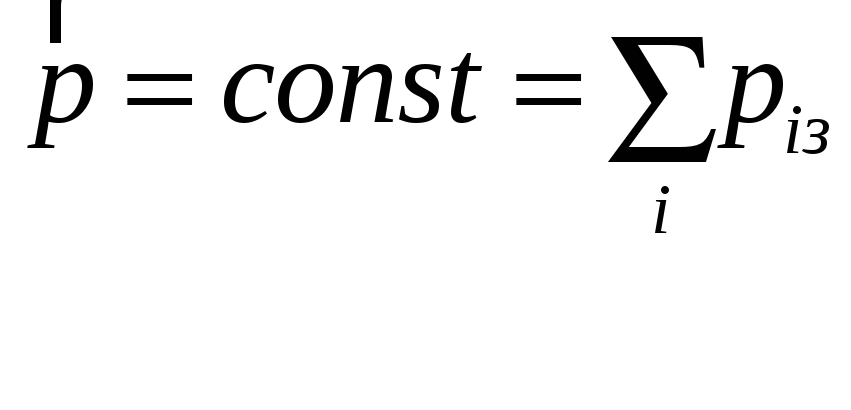
Закон збереження формулюється: у замкненій системі сумарний імпульс усіх тіл зберігається.
Центр мас системи. Рівняння руху центру мас. Це-система.
Центром
мас або центром інерції системи
називається геометрична точка С,
положення якої характеризує розподіл
мас у системі. Положення центра мас
визначається радіус вектором
,
який для системи є дискретним розподілом
мас і системи з неперервним розподілом
описується формулами
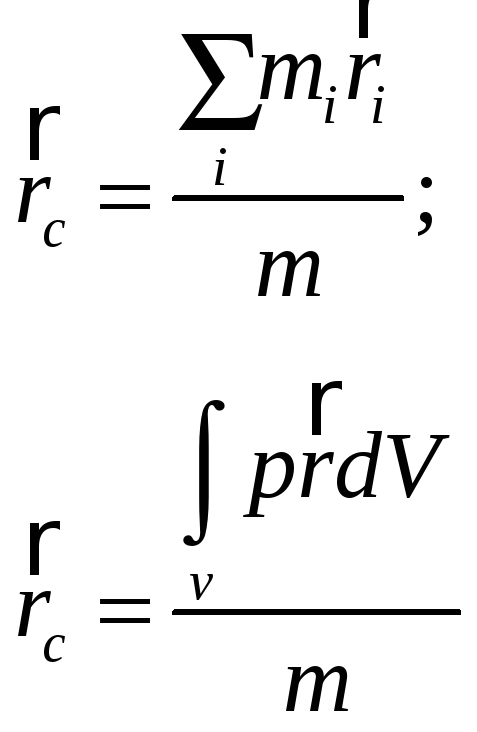
m-маса всієї системи.
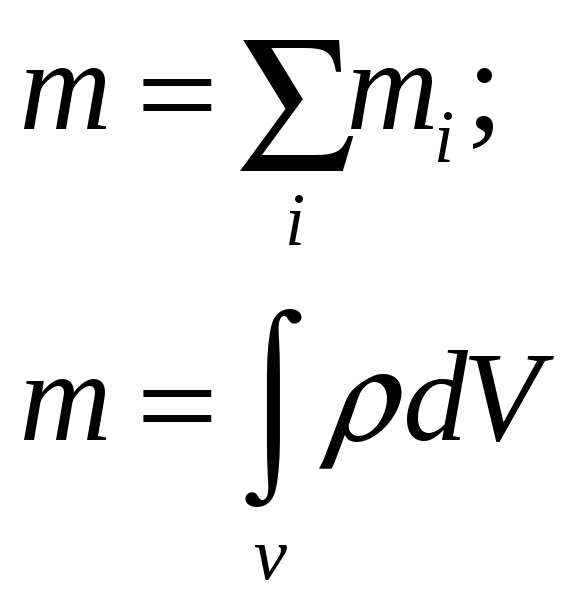
Імпульс центра мас дорівнює повному імпульсу системи. Рух центра мас тотожний з поступальним рухом системи. Якщо на систему діють зовнішні сили, то за другим законом Ньютона отримуємо рівняння руху центра мас
Рух центра мас рухається як матеріальна точка, маса якої дорівнює сумарній масі всієї системи, а діюча сила-геометричній сумі всіх зовнішніх сил, які діють на систему. У замкненій системі імпульс центра мас зберігається:між матеріальними точками системи можуть діяти будь –які сили, система може обертатися,але центр мас системи рухається рівномірно прямолінійно.
Робота сили. Потужність. Робота центральної сили.
Сила,
яка діє на матеріальну точку, та переміщує
її га деяку відстань, виконує над
матеріальною точкою роботу.
Елементарною
роботою dA
сталої
сили
на елементарному переміщенні
називається скалярний добуток сили на
переміщення
Щоб
визначити роботу, яку виконує змінна
над матеріальною точкою при скінченному
переміщенні по траєкторії із положення
до положення
необхідно умовно розбити цей шлях на
нескінченно велике число елементарних
ділянок dS,
у межах кожної з яких
можна
вважати сталою. Робота змінної
вздовж криволінійної траєкторії L
від точки
до точки
,
дорівнює сумі елементарних робіт,
виконаних силою на цьому відрізку
траєкторії, і дорівнює
Інтенсивність виконання характеризують потужністю. Потужністю називається скалярна величина, яка дорівнює роботі, виконаній за одиницю часу
або
Сила називається центральною (потенціальною або консервативною), якщо вона залежить між тілами і діє по лінії, що з’єднує ці тіла.
.
Робота
центру мас залежить тільки від виду
функції
від початкового та кінцевого положення
r,
а від того яким шляхом рухається тіло,
робота не залежить.
Потенціальна енергія. Зв'язок між силою та потенціальною енергією. Градієнт.
Робота центральної сили при переході частинки з положення 1 в положення, умовно прийняте за нульове називають потенціальною енергією. Оскільки робота центральної сили залежить лише від взаємного положення взаємодіючих тіл то потенціальна енергія є функцією від координат.
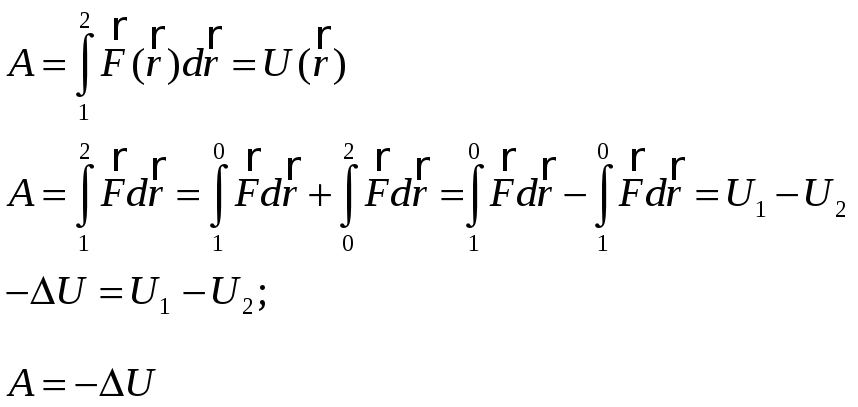
Зв'язок між сило.ю та потенціальною енергією
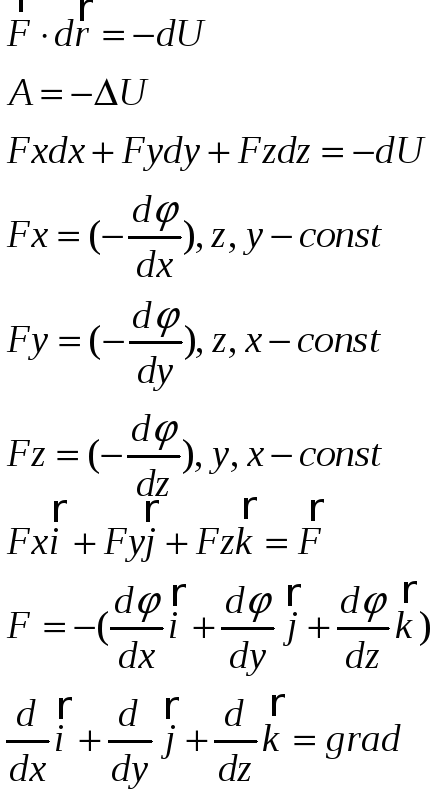(оператор
Набла). Градієнт скалярної функції
Градієнт направлений по нормалі до поверхні рівня (евкіпотеніальна поверхня) в сторону зростання скалярної функціх
