Задание на лабораторную работу №6

Задача 1. Используя табличные данные функции, полученные в соответствии со своим вариантом в лабораторной работе №5, разработать алгоритм и написать по нему программу вычисления производной функции в некоторой точке. Производную считать слева и справа. Результат вывести на экран.

Задача 2. Используя табличные данные функции, полученные в соответствии со своим вариантом в лабораторной работе №5, разработать алгоритм и написать по нему программу вычисления производной на всем интервале задания функции. Результат вывести на экран и в текстовый файл. Построить графики исходной табличной функции и ее производной.

Оформить протокол лабораторной работы.

Примечание! Алгоритмы решения задач должны содержать не только расчетную часть, но и блоки формирования входных и выходных данных, а также блоки проверки правильности вводимых данных.

Контрольные вопросы

1. Что означают термины «производная слева» и «производная справа»?

2. Если табличная функция задана на n точках, в скольких точках можно посчитать производные? Почему?

Лабораторная работа №7

Цель: усовершенствовать навыки программирования на примере решения задач численного интегрирования.

Задачи:

1) Разработать алгоритм и написать по нему программу численного нахождения значения определенного интеграла.

2) Разработать алгоритм и написать по нему программу численного нахождения функции неопределенного интеграла.

Основные теоретические сведения.

Определеный интеграл

Напомним, что интеграл — это предел суммы:

В геометрическом смысле определенный интеграл — это площадь фигуры ограниченной по вертикали кривой функции и осью абсцисс, а по горизонтали —пределами интегрирования. На рис. 20 значение определенного интеграла функции f(x) на отрезке [a,b] численно равно значению суммарной площади затемненных участков.

Рис. 20

Рассмотрим табличную функцию .

xi	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6
f(xi)	0	0.4	0.8	1.2	1.6	2	2.4	2.8	3.2

Пусть необходимо найти значение интеграла от данной функции на отрезке [0; 1.4].

Исходя из определения интеграла, необходимо в каждом частичном интервале выбрать произвольную точку . Произведение:

представляет собой площадь прямоугольника с высотой и шириной . Сумма всех даст искомую площадь под кривой, а следовательно и значение интеграла.

Для простоты, на практике точки часто выбирают равными левой или правой границе частичных интервалов. При этом метод расчет соттветственно называют методом правых и левых прямоугольников. Сказанное поясняет рис. 21

Рис. 21

Пусть точка . Мо можем сформировать прямоугольник как слева от нее, так и справа. Численно площади левого и правого прямоугольников равны. Они отличаются лишь вносимой в расчет погрешностью. Для рассамтриваемого варианта метод левых прямоугольников даст завышеный результат, а метод правых — заниженый.

Воспользуемся формулой для метода правых прямоугольников:

Тогда получим слудующие значения :

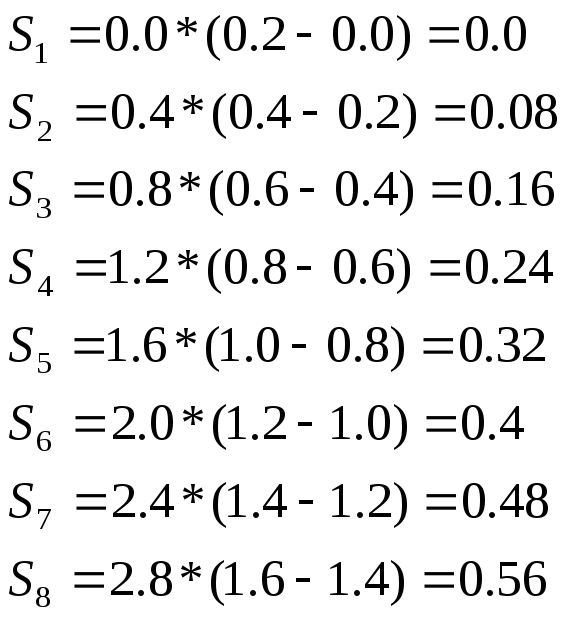
На интересующем нас интервале [0; 1.4] суммарная площадь, а следовательно и значение интеграла будут равны:

0 + 0.08 + 0.16 + 0.24 + 0.32 + 0.4 + 0.48 = 1.68

Так как нам известна исходная аналитическая функция, мы можем сравнить полученный результат с истинным значением. Для этого аналитически возьмем интеграл от функции . Это будет функция . В данном случае константа С нас не интересует. По правилам вычисления определенного интеграла на интервале [0; 1.4] получаем:

Как было отмечено ранее, результат полученный по методу правых прямоугольников оказался заниженным.

Теперь воспользуемся формулой для метода левых прямоугольников:

Тогда:

На интервале [0; 1.4] значение интеграла будет равно:

0.08 + 0.16 + 0.24 + 0.32 + 0.4 + 0.48 + 0.56 = 2.24

Как и ожидалось, результат завышен.