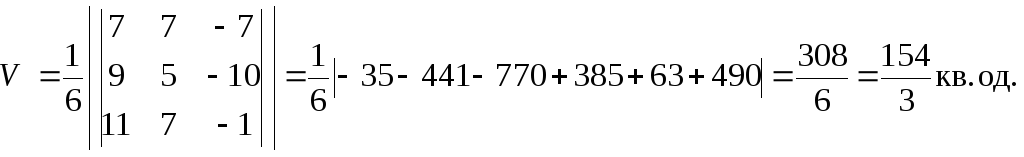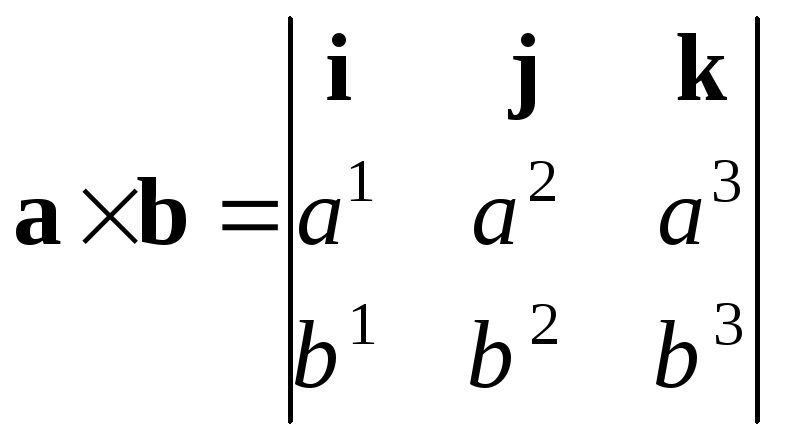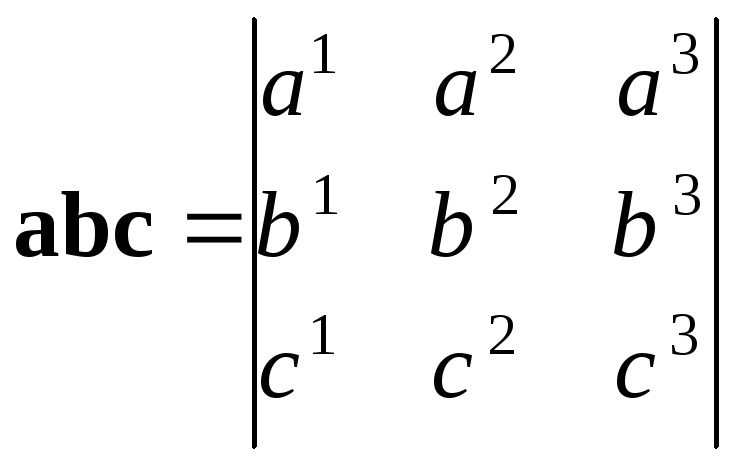- •Лекція 2. Простір геометричних векторів. Добутки векторів.
- •1. Вектори. Операції з векторами.
- •2. Лінійно залежні та лінійно незалежні системи векторів.
- •3. Властивості лінійно залежних та лінійно незалежних систем векторів.
- •4. Базис скінчено вимірного векторного простору. Координати векторів.
- •5. Системи координат в просторі геометричних векторів.
- •6. Добутки векторів.
- •6.1. Скалярний добуток векторів.
- •6.2. Векторний добуток векторів.
- •6.3. Мішаний добуток трьох векторів.
6.2. Векторний добуток векторів.
Означення
16.
Впорядкована трійка некомпланарних
векторів
![]() , приведених до спільного початку,
називається правою
(лівою),
якщо по цим векторам можна спрямувати
відповідно великий, вказівний та середній
пальці правої
(лівої) руки.
Або ж при повороті на найменший кут від
вектору
, приведених до спільного початку,
називається правою
(лівою),
якщо по цим векторам можна спрямувати
відповідно великий, вказівний та середній
пальці правої
(лівої) руки.
Або ж при повороті на найменший кут від
вектору
![]() до вектору
до вектору
![]() напрямок вектору
напрямок вектору
![]() відповідатиме руху правого
(лівого)
гвинта.
(див. мал. нижче). Зрозуміло, що при зміні
напрямку одного з векторів, або при
зміні порядку нумерації двох з векторів
трійка міняє свою орієнтацію на
протилежну. Завжди вважатимемо, що орти
ПДСК мають праву
орієнтацію.
відповідатиме руху правого
(лівого)
гвинта.
(див. мал. нижче). Зрозуміло, що при зміні
напрямку одного з векторів, або при
зміні порядку нумерації двох з векторів
трійка міняє свою орієнтацію на
протилежну. Завжди вважатимемо, що орти
ПДСК мають праву
орієнтацію.
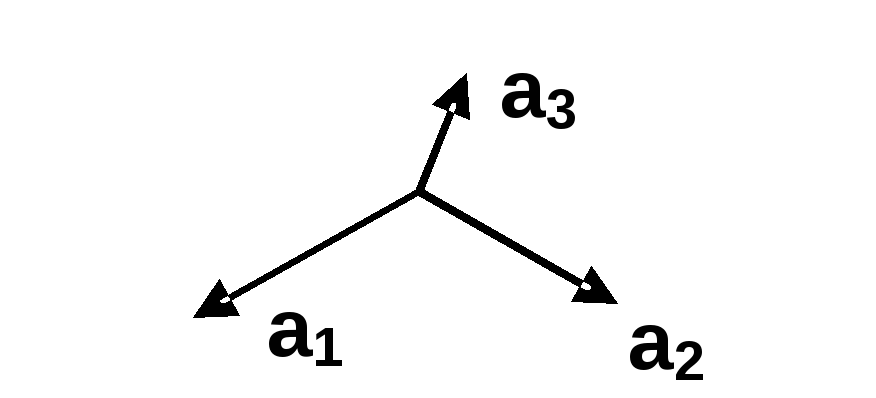
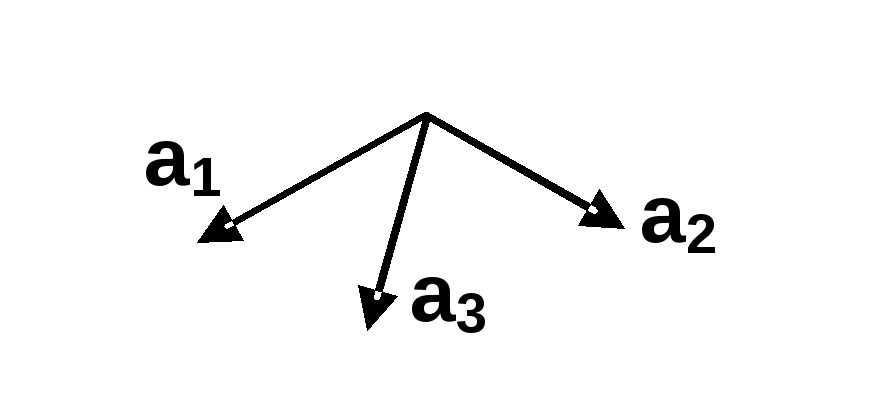
Права трійка векторів Ліва трійка векторів
Означення
17.
Векторним добутком двох векторів
![]() називається вектор
називається вектор
![]() ,
що визначається трьома умовами:
,
що визначається трьома умовами:
-
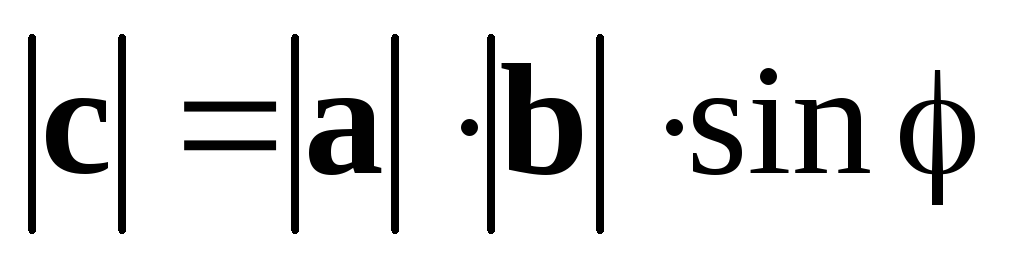 де
де
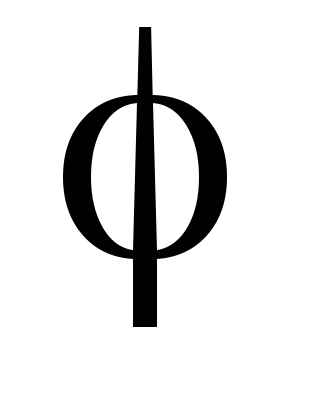 – кут утворений векторами
– кут утворений векторами
 та
та
 ;
; -
вектор ортогональний до обох векторів
 та
та
 ;
; -
вектори
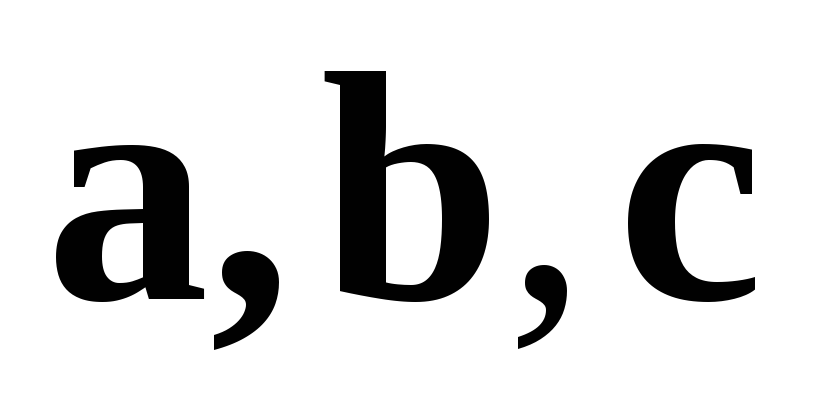 утворюють праву трійку.
утворюють праву трійку.
Для
векторного добутку використовуватимемо
позначення
![]() .
.
Властивості векторного добутку векторів.
-
 – антикомутативність
векторного добутку є наслідком зміни
орієнтації трійки векторів при зміні
їх порядку;
– антикомутативність
векторного добутку є наслідком зміни
орієнтації трійки векторів при зміні
їх порядку; -
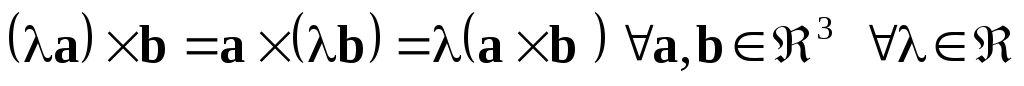 – скалярний
множник можна виносити за знак векторного
добутку (доведіть це самостійно);
– скалярний
множник можна виносити за знак векторного
добутку (доведіть це самостійно); -
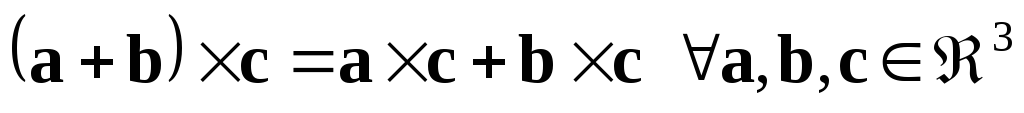 – дистрибутивність
векторного добутку буде
доведена дещо пізніше;
– дистрибутивність
векторного добутку буде
доведена дещо пізніше; -
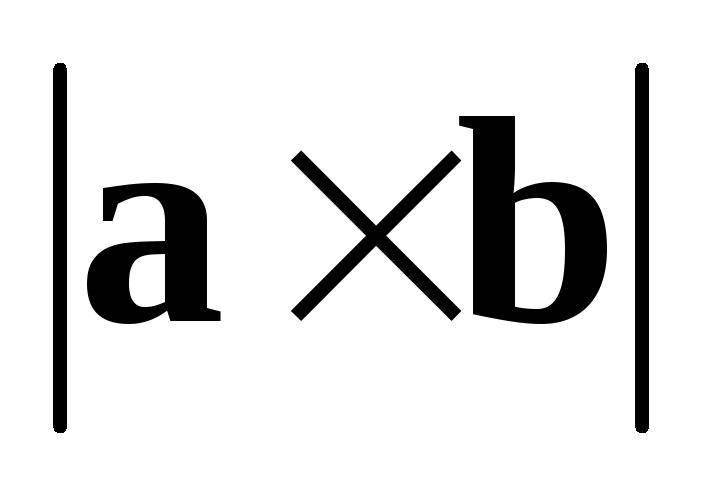 дорівнює
площі паралелограма, побудованого на
векторах
дорівнює
площі паралелограма, побудованого на
векторах
 і
і
 ;
; -
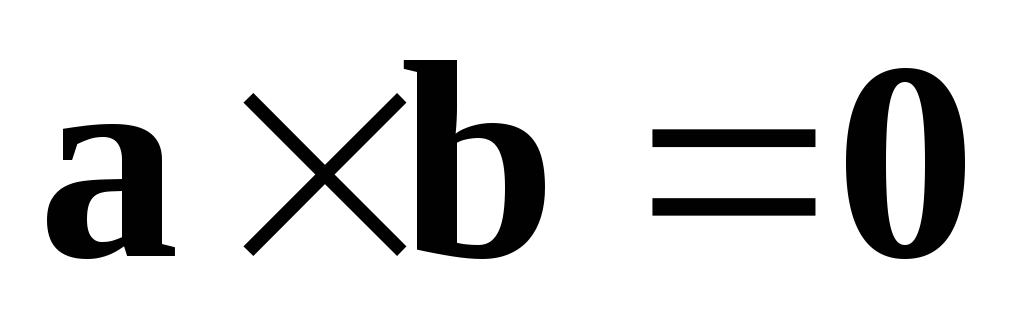 тоді
і тільки тоді, коли вектори
тоді
і тільки тоді, коли вектори
 і
і
 колінеарні або принаймні один з них
нульовий (доведіть це самостійно).
колінеарні або принаймні один з них
нульовий (доведіть це самостійно).
Знайдемо
вираз векторного добутку через координати
векторів-множників. Розглянемо вектори
![]() та
та
![]() .
Визначимо їх векторний добуток,
скориставшись властивостями векторного
добутку та врахувавши, що
.
Визначимо їх векторний добуток,
скориставшись властивостями векторного
добутку та врахувавши, що
![]() :
:
![]() (5)
(5)
Якщо пригадати вигляд формули для обчислення визначника матриці розмірності 3, то можна записати:
|
|
(6)
Приклади.
5. Знайдемо площу трикутника, побудованого на векторах з прикладу 3.
Для цього визначимо спершу векторний добуток даних векторів:
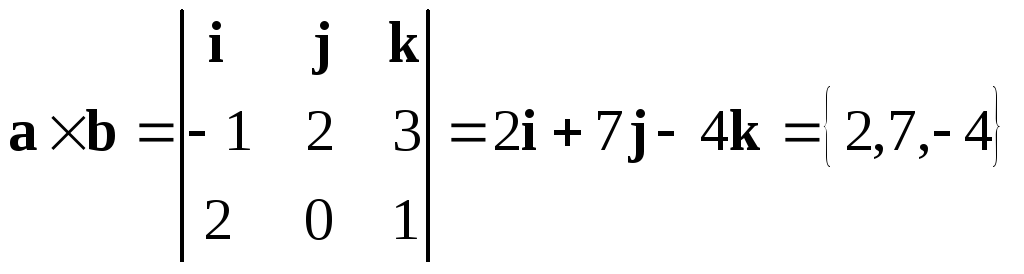
Модуль
цього вектора визначає площу паралелограма,
побудованого на векторах
![]() і
і
![]() ,
отже шукана площа трикутника складає
половину цієї величини:
,
отже шукана площа трикутника складає
половину цієї величини:
![]()
Фізичний зміст векторного добутку.
1
 .
Одним з основних понять статики є момент
сили
.
Одним з основних понять статики є момент
сили
![]() ,
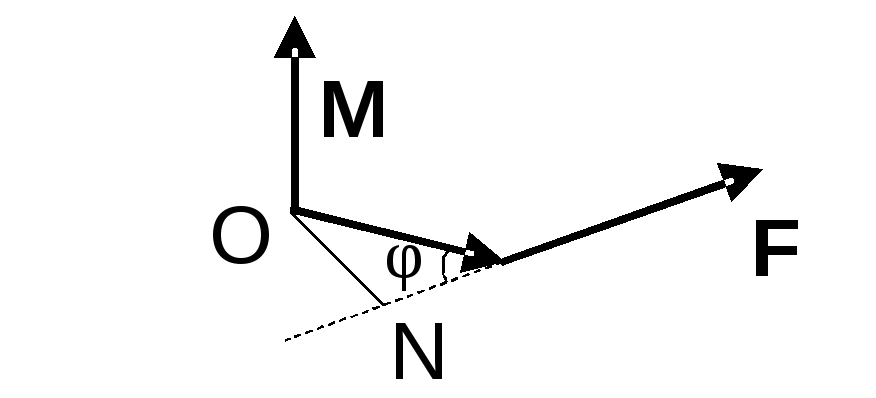
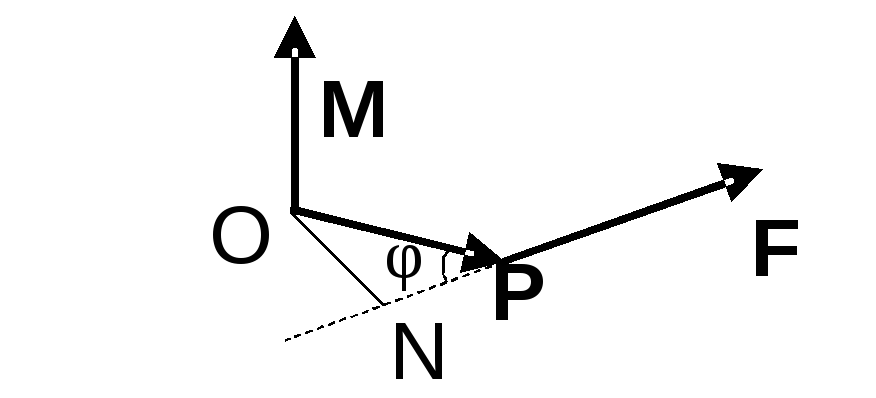
прикладеної до деякої точки Р відносно
фіксованої точки О.
,
прикладеної до деякої точки Р відносно
фіксованої точки О.
Моментом
сили
![]() ,
прикладеної до точки Р відносно фіксованої
точки О, називається вектор
,
прикладеної до точки Р відносно фіксованої
точки О, називається вектор
![]() ,
де
,
де
![]() – радіус-вектор точки Р. За величиною
момент сили рівний
– радіус-вектор точки Р. За величиною
момент сили рівний
![]() – добуток величини сили на плече.
– добуток величини сили на плече.
2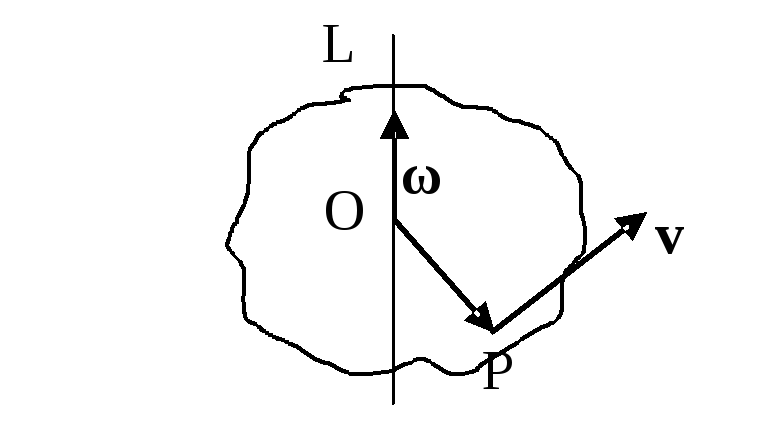 .
Якщо тверде тіло обертається навколо
нерухомої осі
.
Якщо тверде тіло обертається навколо
нерухомої осі
![]() зі сталою кутовою швидкістю
зі сталою кутовою швидкістю
![]() ,
то миттєва швидкість
,
то миттєва швидкість
![]() довільної точки Р цього тіла, як відомо,
визначається формулою
Ейлера:
довільної точки Р цього тіла, як відомо,
визначається формулою
Ейлера:
![]() , де
, де
![]() – радіус-вектор точки Р відносно полюса
О на осі обертання
– радіус-вектор точки Р відносно полюса
О на осі обертання
![]() .
Напрямлений
вектор швидкості по дотичній до кола,
по якому рухається точка Р у бік обертання.
.
Напрямлений
вектор швидкості по дотичній до кола,
по якому рухається точка Р у бік обертання.
6.3. Мішаний добуток трьох векторів.
Означення
18.
Мішаним
добутком впорядкованої трійки векторів
![]() називається число, рівне
називається число, рівне
![]() .
.
Якщо
кут між векторами
![]() та
та
![]() позначити
позначити
![]() ,
а кут між векторним добутком
,
а кут між векторним добутком
![]() та вектором
та вектором
![]() –
–
![]() ,
то значення мішаного добутку можна
обрахувати наступним чином:
,
то значення мішаного добутку можна
обрахувати наступним чином:
![]() (7)
(7)
Властивості мішаного добутку векторів.
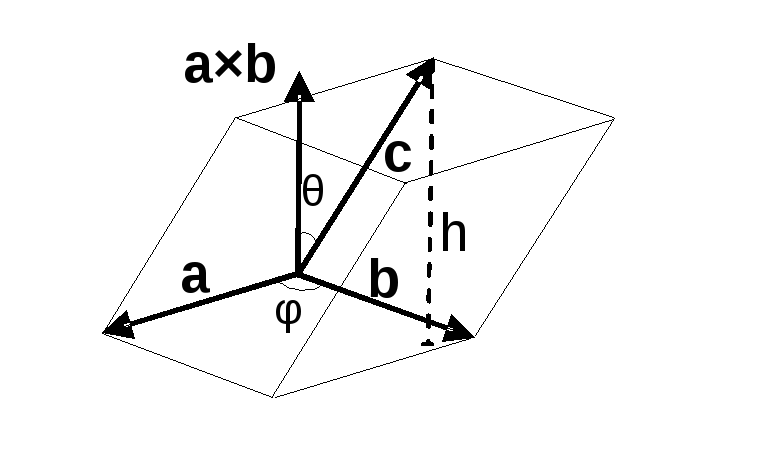
-
Мішаний добуток правої трійки векторів
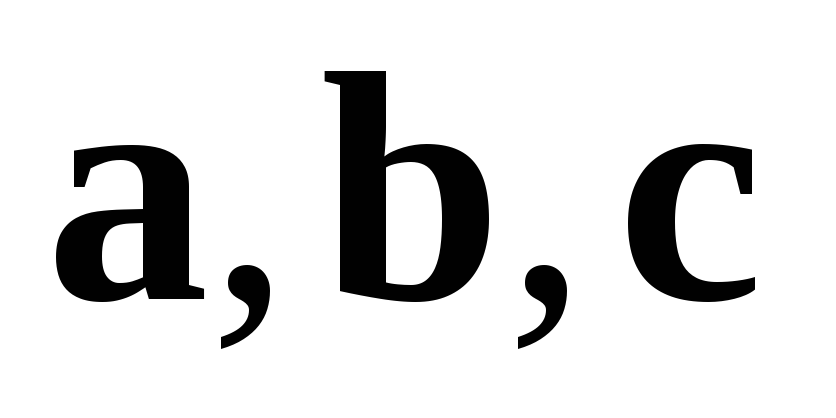 дорівнює об’єму паралелепіпеда,
побудованого на цих векторах.
Це очевидно (див.
мал.), оскільки площа основи такого
паралелепіпеда рівна
дорівнює об’єму паралелепіпеда,
побудованого на цих векторах.
Це очевидно (див.
мал.), оскільки площа основи такого
паралелепіпеда рівна
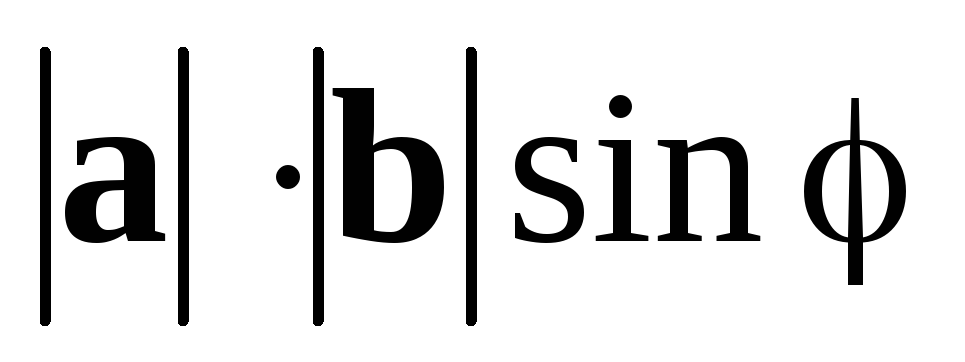 ,
а висота
,
а висота
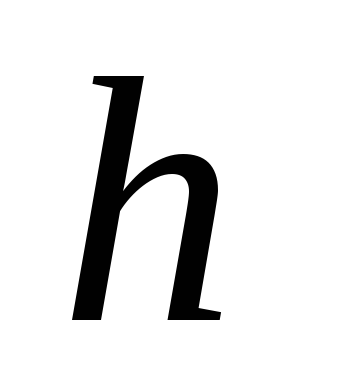 рівна
рівна
 .
Отже,
.
Отже,
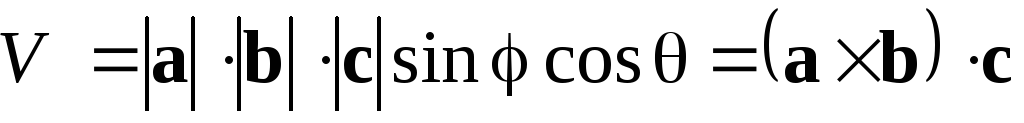 .
Проте, у випадку лівої трійки векторів
кут
.
Проте, у випадку лівої трійки векторів
кут
 виявиться тупим і для визначення об’єму
паралелепіпеда треба використовувати
модуль мішаного добутку
виявиться тупим і для визначення об’єму
паралелепіпеда треба використовувати
модуль мішаного добутку
 .
Крім того, очевидно, що знак мішаного
добутку визначає орієнтацію трійки
векторів: якщо
.
Крім того, очевидно, що знак мішаного
добутку визначає орієнтацію трійки
векторів: якщо
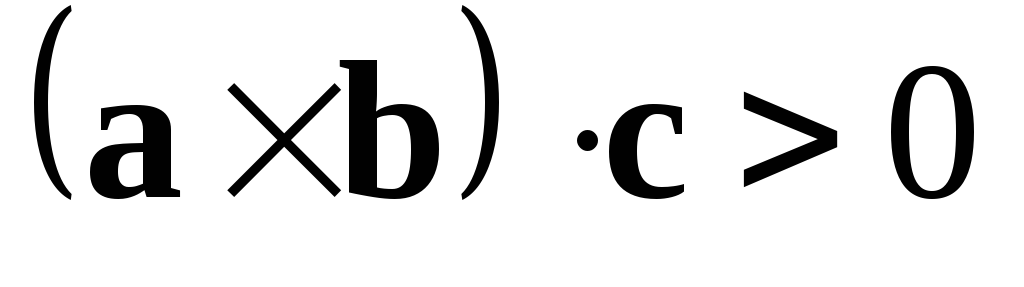 ,
то трійка векторів права, інакше трійка
ліва. Якщо ж вектори компланарні, тобто
паралельні одній площині, то висота
такого «паралелепіпеда» рівна 0, отже
нулю рівний і його об’єм.
,
то трійка векторів права, інакше трійка
ліва. Якщо ж вектори компланарні, тобто
паралельні одній площині, то висота
такого «паралелепіпеда» рівна 0, отже
нулю рівний і його об’єм.
-
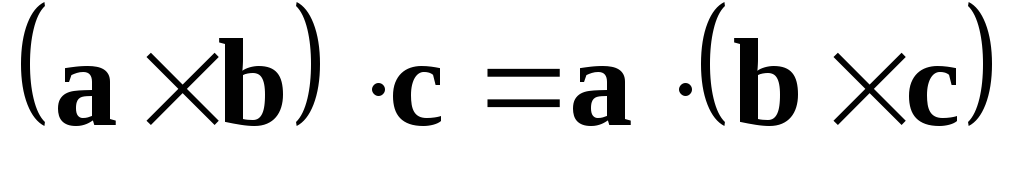 (8)
(8)
Дійсно,
площу паралелограма можна визначити,
взявши за основу іншу грань, наприклад,
утворену векторами
![]() та
та
![]() . Тоді маємо
. Тоді маємо
![]() .
А
оскільки
орієнтація трійки
.
А
оскільки
орієнтація трійки
![]() така сама, як і трійки
така сама, як і трійки
![]() ,
то таким чином, бачимо, що у мішаному
добутку векторів
,
то таким чином, бачимо, що у мішаному
добутку векторів
![]() не має значення, до якої пари множників
не має значення, до якої пари множників
![]() і
і
![]() чи
чи
![]() і
і
![]() застосовувати векторне множення. Власне
тому мішаний добуток просто позначають
застосовувати векторне множення. Власне
тому мішаний добуток просто позначають
![]() ,
оскільки важливим виявляється лише
порядок множників.
,
оскільки важливим виявляється лише
порядок множників.
-
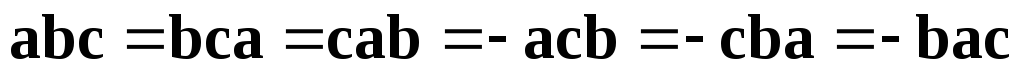 (9)
(9)
Дана властивість легко випливає із узагальнення властивості 2 та антикомутативності векторного добутку.
-
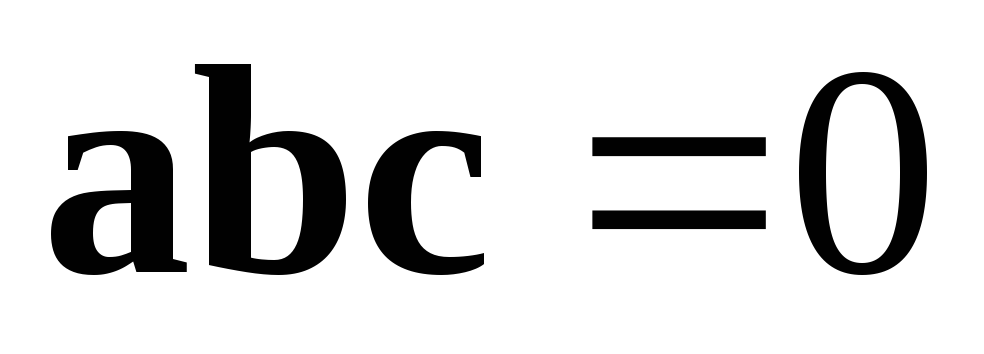 тоді
і тільки тоді, коли вектори
тоді
і тільки тоді, коли вектори
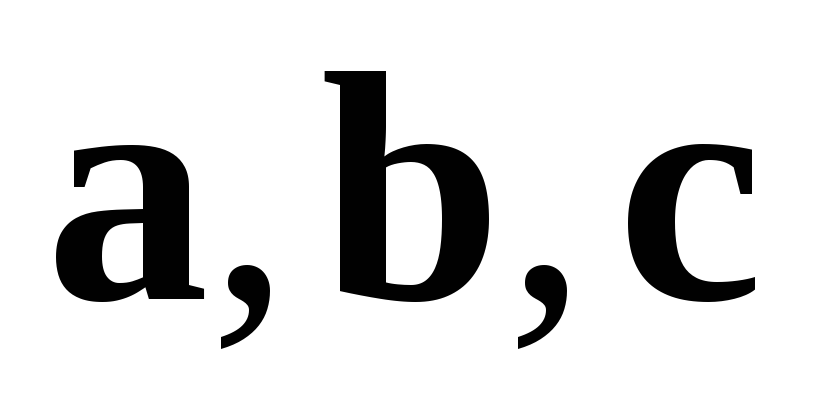 компланарні.
компланарні.
Достатність
цього твердження була обґрунтована при
доведенні першої властивості, тому
доведемо тут необхідність. Отже, нехай
![]() .
Якщо принаймні один з множників є
нуль-вектором, то трійка напевне
компланарна, тому далі вважатимемо, що
всі вектори-множникі ненульові. У такому
випадку із формули (7) випливає, що кут
.
Якщо принаймні один з множників є
нуль-вектором, то трійка напевне
компланарна, тому далі вважатимемо, що
всі вектори-множникі ненульові. У такому
випадку із формули (7) випливає, що кут
![]() – це означає компланарність векторів,
або ж кут
– це означає компланарність векторів,
або ж кут
![]() .
В цьому разі вектори
.
В цьому разі вектори
![]() і
і
![]() колінеарні, що також означає компланарність
векторів
колінеарні, що також означає компланарність
векторів
![]() .
.
Дана властивість є наслідком відповідних властивостей скалярного та векторного добутків.
![]() – дистрибутивність
мішаного добутку.
– дистрибутивність
мішаного добутку.
Знайдемо
тепер вираз мішаного добутку через
координати векторів-множників. Розглянемо
вектори
![]() ,
,
![]() та
та
![]() .
Визначимо їх мішаний добуток.
.
Визначимо їх мішаний добуток.
Оскільки
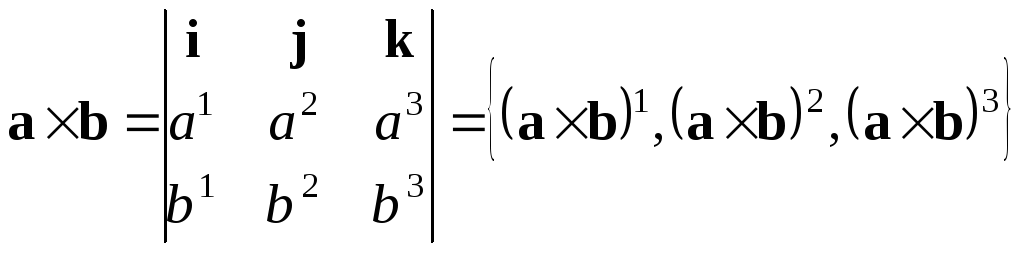 ,
а
,
а
![]() ,
то
,
то
 .
Остаточно одержуємо формулу
.
Остаточно одержуємо формулу
|
|
(10)
Зауваження. З формули (10) та властивості 3 мішаного добутку випливає, що визначник матриці розмірності 3 не зміниться при циклічній перестановці рядків і змінить знак на протилежний при перестановці двох рядків.
Приклади.
6.
Знайдемо
об’єм тетраедра з вершинами
![]() .
.
Даний
тетраедр утворений векторами
![]() .
Оскільки орієнтація цієї трійки нам
невідома, об’єм тетраедра визначатимемо
як
.
Оскільки орієнтація цієї трійки нам
невідома, об’єм тетраедра визначатимемо
як
![]() модуля мішаного добутку векторів
модуля мішаного добутку векторів
![]() :
: