
Лекція 3. Площина та пряма в геометричному просторі.
1. Площина.
П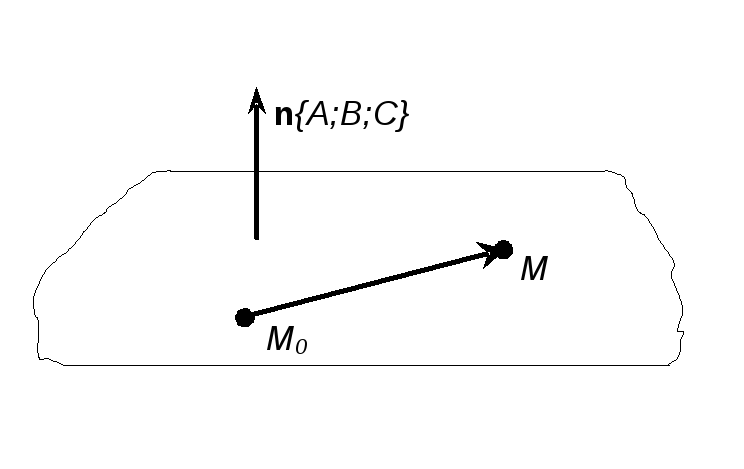
 оняття
площини є одним із первісних геометричних
понять. Вважатимемо, що у просторі обрана
та зафіксована деяка ПДСК. Якщо визначити
деякий напрямок з допомогою, наприклад,
вектора
оняття
площини є одним із первісних геометричних
понять. Вважатимемо, що у просторі обрана
та зафіксована деяка ПДСК. Якщо визначити
деякий напрямок з допомогою, наприклад,
вектора
![]() ,
то тим самим визначена множина площин,
перпендикулярних даному напрямку.
Вектор
,
то тим самим визначена множина площин,
перпендикулярних даному напрямку.
Вектор
![]() зветься нормаллю
цих площин. Щоб визначити серед цієї
множини конкретну площину, досить
вказати точку
зветься нормаллю
цих площин. Щоб визначити серед цієї
множини конкретну площину, досить
вказати точку
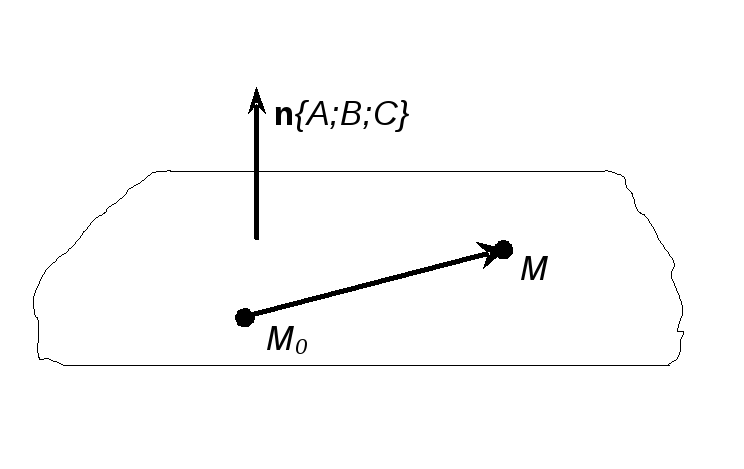
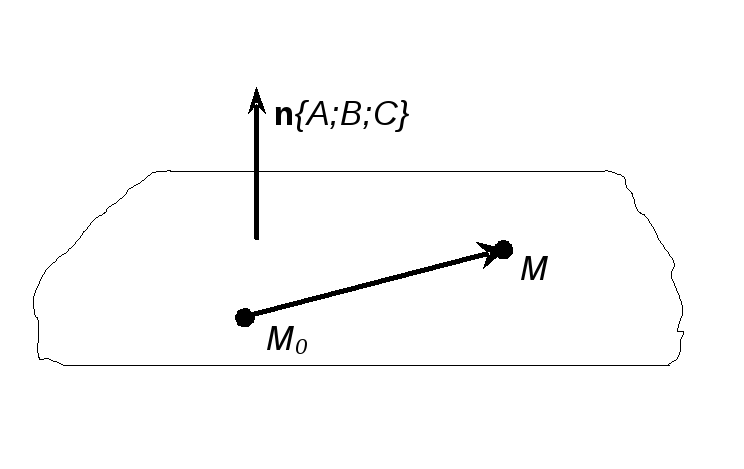
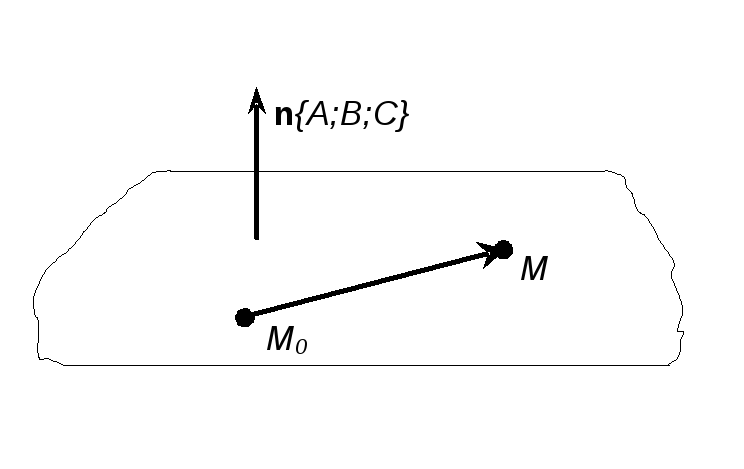
![]() на ній (див рис. 1). Позначимо
на ній (див рис. 1). Позначимо
![]() довільну точку цієї площини. Тоді вектори
довільну точку цієї площини. Тоді вектори
![]() та
та
![]() будуть ортогональними, а отже,
будуть ортогональними, а отже,
![]() (1)
(1)
є
векторним рівнянням площини. Тут
![]() та
та
![]() – відповідно радіус-вектори точок
– відповідно радіус-вектори точок
![]() та
та
![]() .
Записавши рівність (1) у координатній
формі, матимемо
рівняння
площини, заданої точкою та нормаллю:
.
Записавши рівність (1) у координатній
формі, матимемо
рівняння
площини, заданої точкою та нормаллю:
Рис.
1 ![]() (2)
(2)
Рівняння
(2), яке задає площину, є рівнянням першого
порядку виду
![]() (3)
(3)
Покажемо,
що й навпаки, будь-яке рівняння першого
порядку (3) визначає деяку площину у
просторі. З цією метою розглянемо точку
![]() ,
яка задовольняє рівняння (3). Для неї
виконана рівність
,
яка задовольняє рівняння (3). Для неї
виконана рівність
![]() .
Віднявши її від рівняння (3), одержимо
рівність (2), яка виражає умову
ортогональності вектора
.
Віднявши її від рівняння (3), одержимо
рівність (2), яка виражає умову
ортогональності вектора
![]() ,
який належить розглядуваному геометричному
об’єкту, та деякого фіксованого вектора
,
який належить розглядуваному геометричному
об’єкту, та деякого фіксованого вектора
![]() .
Отже, рівняння (3) задає деяку площину.
Воно називається загальним
рівнянням площини.
Дослідимо частинні випадки цього
рівняння, коли деякі коефіцієнти в ньому
рівні нулеві.
.
Отже, рівняння (3) задає деяку площину.
Воно називається загальним
рівнянням площини.
Дослідимо частинні випадки цього
рівняння, коли деякі коефіцієнти в ньому
рівні нулеві.
-
Припустимо, що
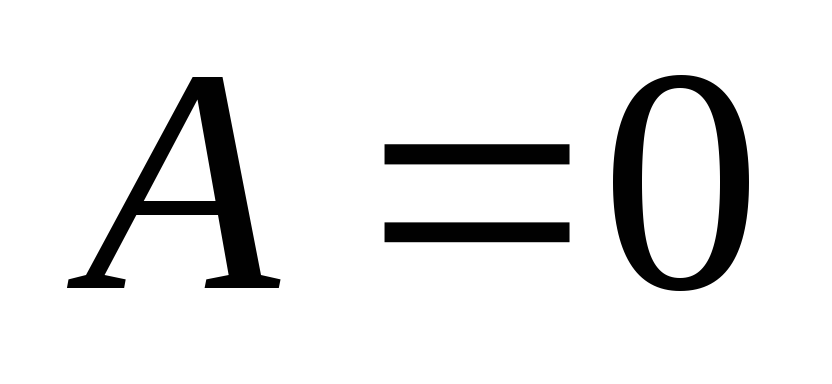 .
Тоді вектор нормалі площини, очевидно,
ортогональний до осі ОХ, а сама площина
їй паралельна.
.
Тоді вектор нормалі площини, очевидно,
ортогональний до осі ОХ, а сама площина
їй паралельна. -
Припустимо, що
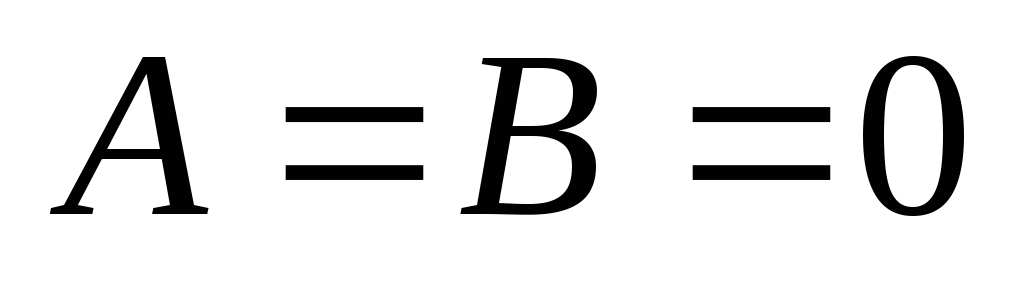 .
Тоді площина паралельна обом осям і
ОХ, і OY,
тобто паралельна координатній площині
ХOY
і перпендикулярна осі ОZ.
.
Тоді площина паралельна обом осям і
ОХ, і OY,
тобто паралельна координатній площині
ХOY
і перпендикулярна осі ОZ. -
Нехай
 .
Дана площина проходить через початок
координат – точку
.
Дана площина проходить через початок
координат – точку
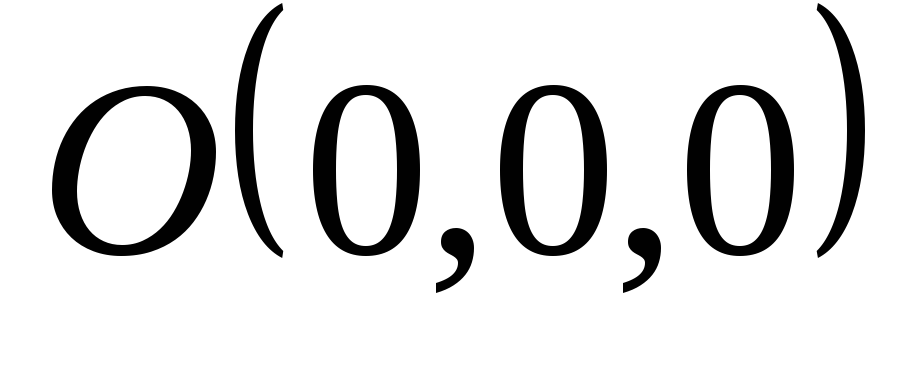 .
. -
Припустимо, що
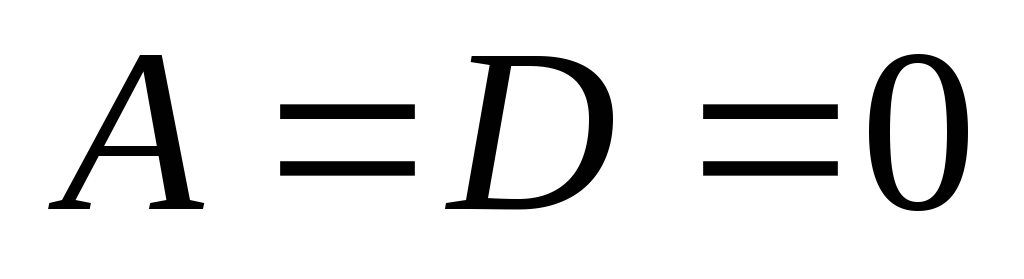 – площина паралельна осі ОХ та проходить
через початок координат, отже, вісь ОХ
належить площині.
– площина паралельна осі ОХ та проходить
через початок координат, отже, вісь ОХ
належить площині. -
Якщо
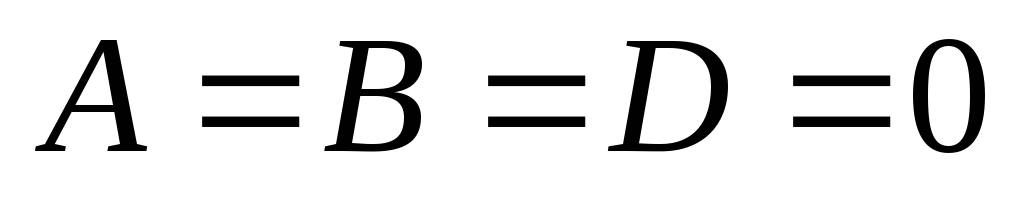 ,
то маємо рівняння
,
то маємо рівняння
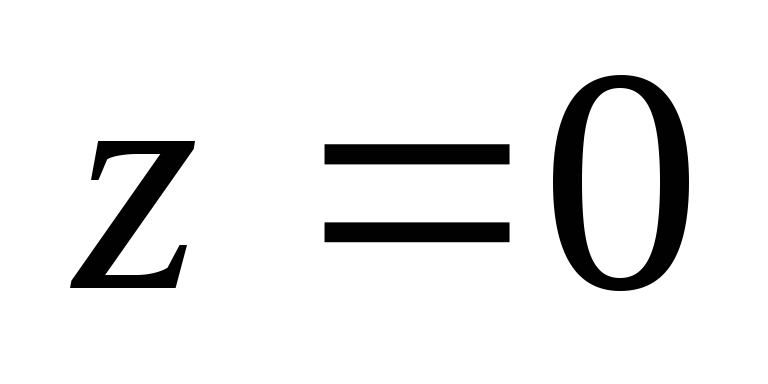 ,
яке задає координатну площину ХOY.
,
яке задає координатну площину ХOY.
П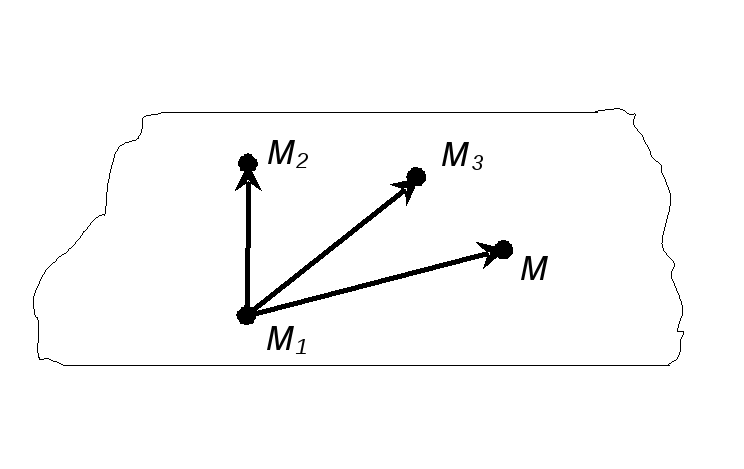 лощина
також може бути визначена трьома своїми
точками. Нехай
лощина
також може бути визначена трьома своїми
точками. Нехай
![]() ,
,
![]() та
та
![]() – три точки відповідно з радіус-векторами
– три точки відповідно з радіус-векторами
![]() ,
,
![]() та
та
![]() ,
які визначають деяку площину (див. рис.
2). Щоб записати її рівняння розглянемо
довільну точку
,
які визначають деяку площину (див. рис.
2). Щоб записати її рівняння розглянемо
довільну точку
![]() цієї ж площини.
Тоді
вектори
цієї ж площини.
Тоді
вектори
![]() ,
,
![]() та
та
![]() – компланарні, отже, їх мішаний
добуток
нульовий, тобто
– компланарні, отже, їх мішаний
добуток
нульовий, тобто
![]() (4)
(4)
Рис.
2 є
векторним рівнянням
площини, заданої трьома точками.
Відповідне рівняння у координатній
формі має вигляд: 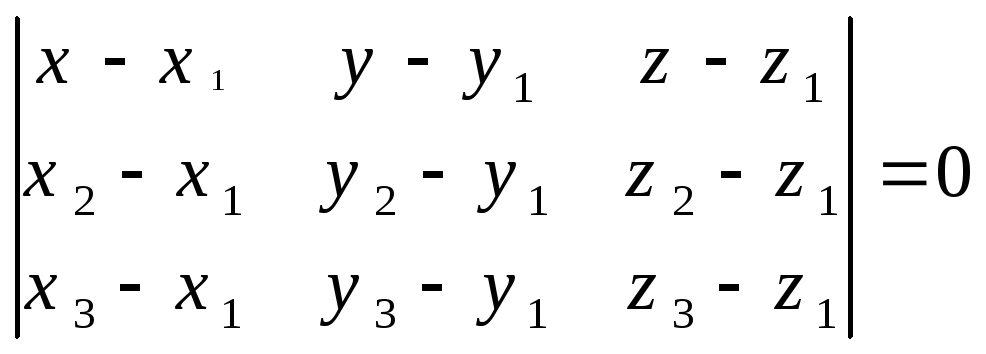 (5)
(5)
Приклад
1.
Знайти рівняння площини, що проходить
через початок координат перпендикулярно
до вектора
![]() .
.
Заданий
вектор
![]() є нормаллю даної площини, а оскільки
початок координат належить площині, в
загальному рівнянні (3) слід покласти
є нормаллю даної площини, а оскільки
початок координат належить площині, в
загальному рівнянні (3) слід покласти
![]() .
Таким чином, шукане рівняння має вигляд
.
Таким чином, шукане рівняння має вигляд
![]() .
.
Приклад
2.
Скласти рівняння площини, що проходить
через три дані точки
![]() ,
,
![]() та
та
![]() .
.
Запишемо
рівняння площини у вигляді (5):
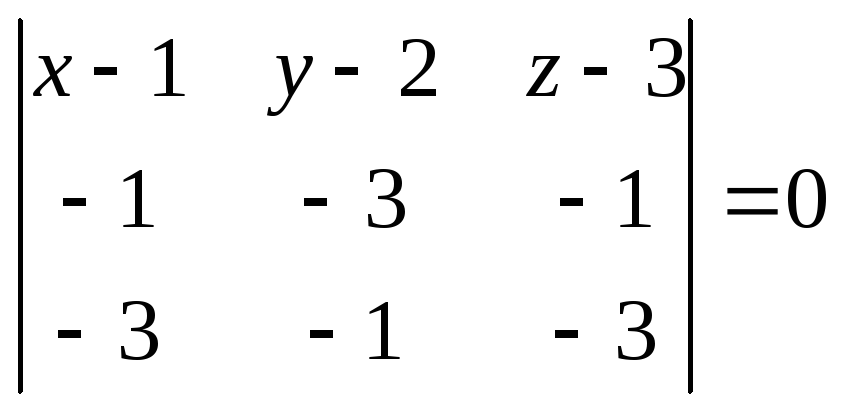 ,
або
,
або
![]() ,
або нарешті,
,
або нарешті,
![]() .
.
Припустимо,
що площина (3) не проходить через початок
координат, тобто коефіцієнт
![]() ,
тоді рівняння площини можна подати у
вигляді:
,
тоді рівняння площини можна подати у
вигляді:
![]() , або
, або ![]() ,
(6)
,
(6)
де
![]() – відповідно точок перетину площини
(3) з осями ОХ, OY
та ОZ.
Зверніть увагу, якщо, наприклад,
– відповідно точок перетину площини
(3) з осями ОХ, OY
та ОZ.
Зверніть увагу, якщо, наприклад,
![]() ,
то координату точки перетину площини
із віссю ОХ визначити неможливо –
площина їй паралельна. Рівняння (6) носить
назву рівняння площини у
відрізках на осях.
,
то координату точки перетину площини
із віссю ОХ визначити неможливо –
площина їй паралельна. Рівняння (6) носить
назву рівняння площини у
відрізках на осях.
Двогранний
кут
![]() між двома площинами, заданими рівняннями
між двома площинами, заданими рівняннями
![]()
![]() ,
можна визначити як кут між їх нормалями
,
можна визначити як кут між їх нормалями
![]() та
та
![]() :
:
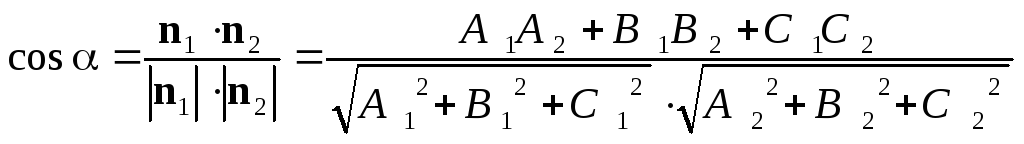 (7)
(7)
Зауваження.
Зрозуміло, що таким чином буде визначений
лише один з двох двогранних кутів, інший
рівний
![]() .
.
З
формули (7) випливає умова
перпендикулярності двох площин,
а саме: дві площини перпендикулярні
тоді і тільки тоді, коли ![]() . (8)
. (8)
Умова
паралельності двох площин
еквівалентна умові колінеарності їх
нормалей:
![]() .
(9)
.
(9)
Приклад
3.
Визначити кути між площинами
![]() та
та
![]() .
.
Нормалями
до заданих площин є вектори
![]() та
та
![]() .
Легко переконатись, що скалярний добуток
цих векторів рівний нулю, тобто виконана
умова (8):
.
Легко переконатись, що скалярний добуток
цих векторів рівний нулю, тобто виконана
умова (8):
![]() – площини перпендикулярні.
– площини перпендикулярні.
Приклад
4.
Скласти рівняння площини, що проходить
через точку
![]() перпендикулярно до площин
перпендикулярно до площин
![]() та
та
![]() .
.
Оскільки
шукана площина перпендикулярна до
площин з нормалями
![]() та
та
![]() ,
то її нормаль
,
то її нормаль
![]() є перпендикулярною до обох нормалей
є перпендикулярною до обох нормалей
![]() та
та
![]() ,
а отже, колінеарна їх векторному добутку
,
а отже, колінеарна їх векторному добутку
![]() .
Визначимо
.
Визначимо
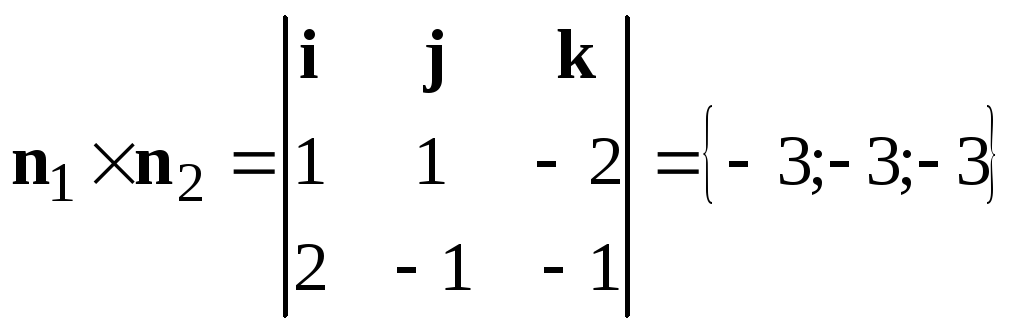 .
Таким чином, можна вважати, що
.
Таким чином, можна вважати, що
![]() .
Шукана площина тепер визначається
рівнянням (2):
.
Шукана площина тепер визначається
рівнянням (2):
![]() ,
або
,
або
![]() .
.
Приклад
5.
Знайти об’єм тетраедра, утвореного
координатними площинами та площиною
![]() .
.
Запишемо
рівняння даної площини у вигляді рівняння
(6), перенісши вільний член у праву частину
та поділивши обидві частини рівняння
на -12. Одержимо рівняння
![]() .
Отже, прямокутний тетраедр має ребра з
довжинами
.
Отже, прямокутний тетраедр має ребра з
довжинами
![]() ,
,
![]() та
та
![]() .
Його об’єм рівний 12 кубічним одиницям.
звідки
.
Його об’єм рівний 12 кубічним одиницям.
звідки
![]() .
Отже, шукана площина визначається
рівнянням
.
Отже, шукана площина визначається
рівнянням
![]() .
.
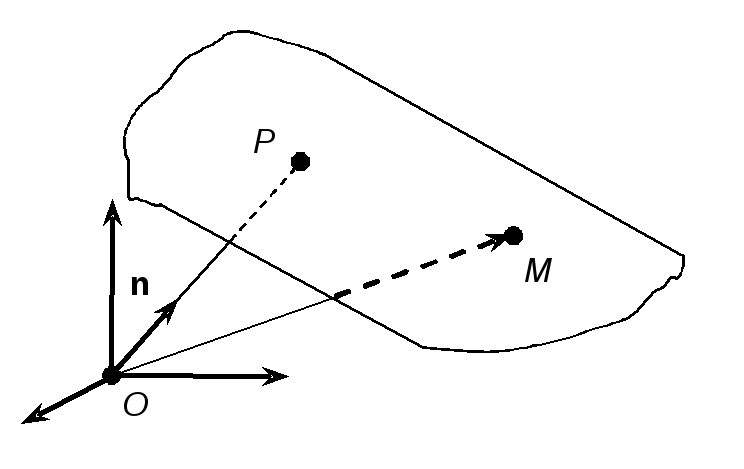
Розглянемо
далі (рис. 3) орт
![]() нормалі, проведеної
із початку координат до площини.
нормалі, проведеної
із початку координат до площини.
 Якщо
позначити через
Якщо
позначити через
![]() відстань від початку координат до
площини,
то
для довільної точки
відстань від початку координат до
площини,
то
для довільної точки
![]() площини маємо рівність
площини маємо рівність
![]() ,
або
,
або ![]() (10)
(10)
Дане
рівняння називається нормальним
рівнянням площини,
оскільки в ньому фігурує орт особливої
нормалі площини – проведеної із початку
координат. Щоб записати рівняння (3) у
нормальній
формі,
необхідно помножити обидві частини
рівняння на коефіцієнт
![]() ,
Рис. 3 підібравши знак так, щоб виконувалось
,
Рис. 3 підібравши знак так, щоб виконувалось
![]() .
.
Н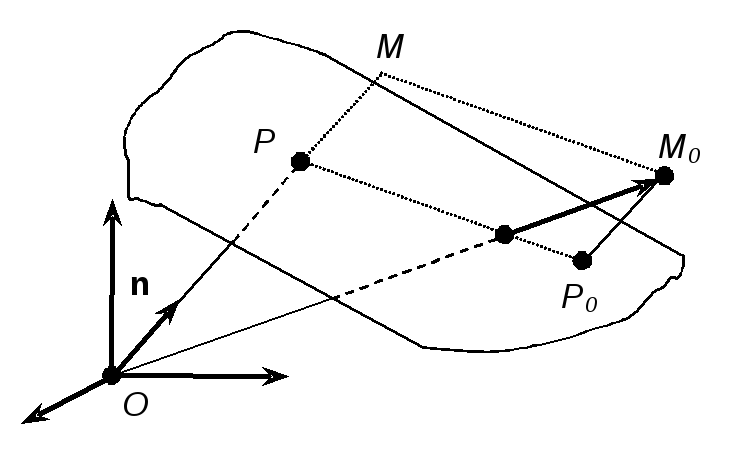 ехай
ехай
![]() – довільна точка простору, яка розташована
з протилежного боку ніж початок координат
відносно площини. Тоді для неї справджується
очевидна рівність (див рис. 4):
– довільна точка простору, яка розташована
з протилежного боку ніж початок координат
відносно площини. Тоді для неї справджується
очевидна рівність (див рис. 4):
![]() ,
де
,
де
![]() – відстань від точки
– відстань від точки
![]() до
площини.
Отже, в цьому випадку маємо
до
площини.
Отже, в цьому випадку маємо
![]() .
Якщо точка
.
Якщо точка
![]() розташована по той самий бік від площини,
що й початок координат, то аналогічними
міркуваннями (зробіть малюнок самостійно)
доходимо висновку, що
розташована по той самий бік від площини,
що й початок координат, то аналогічними
міркуваннями (зробіть малюнок самостійно)
доходимо висновку, що
![]() ,
отже,
,
отже,
![]() .
Введемо у розгляд величину
.
Введемо у розгляд величину ![]() .
(11)
.
(11)
Вона
зветься відхиленням
точки
![]() від площини і є результатом підстановки
її координат у нормаль-
від площини і є результатом підстановки
її координат у нормаль-
не
рівняння площини (10). Відхилення точки
![]() додатне,
якщо точка та початок координат
розташовані по різні боки від площини
і від’ємне,
якщо точка
додатне,
якщо точка та початок координат
розташовані по різні боки від площини
і від’ємне,
якщо точка
![]() та початок координат розташовані по
один бік площини. У будь-якому випадку,
та початок координат розташовані по
один бік площини. У будь-якому випадку,
![]() .
.
Приклад
6.
Знайти відстань та відхилення точки
![]() від площини
від площини
![]() .
.
Довжина
нормалі заданої площини дорівнює
![]() .
Щоб записати нормальне рівняння цієї
площини, досить поділити обидві частини
заданого рівняння на коефіцієнт
.
Щоб записати нормальне рівняння цієї
площини, досить поділити обидві частини
заданого рівняння на коефіцієнт
![]() .
Отже, нормальне рівняння матиме вигляд:
.
Отже, нормальне рівняння матиме вигляд:
![]() .
Визначимо відхилення точки
.
Визначимо відхилення точки
![]() :
:
![]() –
точка
та початок координат знаходяться по
один бік площини; відстань точки
–
точка
та початок координат знаходяться по
один бік площини; відстань точки
![]() від площини рівна
від площини рівна
![]() .
.
Приклад
7.
Скласти рівняння площин, паралельних
площині
![]() та розташованих на відстані
та розташованих на відстані
![]() одиниць від неї.
одиниць від неї.
Щоб
записати нормальне рівняння цієї
площини, досить поділити обидві частини
заданого рівняння на коефіцієнт
![]() ,
причому знак треба вибрати так, щоб
вільний член нормального рівняння був
від’ємним. Отже, нормальне рівняння
заданої площини матиме вигляд:
,
причому знак треба вибрати так, щоб
вільний член нормального рівняння був
від’ємним. Отже, нормальне рівняння
заданої площини матиме вигляд:
![]() .
Тому рівняння паралельних площин, які
розташовані на відстані
.
Тому рівняння паралельних площин, які
розташовані на відстані
![]() одиниць від неї, матимуть вигляд:
одиниць від неї, матимуть вигляд:
![]() .
Таким чином, шуканими є площини
.
Таким чином, шуканими є площини
![]() та
та
![]() .
.
