21. Метод вариации произвольных постоянных.

a_n(t)z⁽ⁿ⁾(t) + a_{n − 1}(t)z^{(n − 1)}(t) + ... + a₁(t)z'(t) + a₀(t)z(t) = f(t)

состоит в замене произвольных постоянных c_k в общем решении

z(t) = c₁z₁(t) + c₂z₂(t) + ... + c_nz_n(t)

соответствующего однородного уравнения

a_n(t)z⁽ⁿ⁾(t) + a_{n − 1}(t)z^{(n − 1)}(t) + ... + a₁(t)z'(t) + a₀(t)z(t) = 0

на вспомогательные функции c_k(t), производные которых удовлетворяют линейной алгебраической системе

Определителем системы (1) служит вронскиан функций z₁,z₂,...,z_n, что обеспечивает её однозначную разрешимость относительно .

Если  — первообразные для , взятые при фиксированных значениях постоянных интегрирования, то функция

является решением исходного линейного неоднородного дифференциального уравнения. Интегрирование неоднородного уравнения при наличии общего решения соответствующего однородного уравнения сводится, таким образом, к квадратурам.

23.Лоду с постоянными коэфициентами.

Однородное линейное дифференциальное уравнение

где  -- функции от , имеет общее решение вида

где , ,...,  -- линейно независимые частные решения дифференциального уравнения, а , ,...,  -- произвольные постоянные.

Если коэффициенты , ,..., постоянны, то частные решения , ,..., могут быть найдены с помощью характеристического уравнения

Каждому вещественному корню этого уравнения кратности соответствуют частных линейно независимых решений дифференциального уравнения , ,..., . Каждой паре сопряженных комплексных корней кратности соответствуют пар частных решений , ,..., , , ,..., . Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Для решения неоднородного линейного дифференциального уравнения с постоянными коэффициентами

необходимо найти общее решение соответствующего однородного уравнения

а также одно частное решение неоднородного уравнения. Тогда общее решение неоднородного дифференциального уравнения имеет вид

Для поиска частного решения неоднородного уравнения в случае, если  -- постоянные, можно использовать метод неопределенных коэффициентов. А именно, если является многочленом от с постоянными коэффициентами, либо , либо есть сумма или произведение указанных функций, то частное решение можно искать в таком же виде, но с другими коэффициентами, подлежащими определению. Исключение составляют особые (резонансные) случаи, когда либо 1)  -- многочлен, и является корнем кратности характеристического уравнения, либо 2) , и являются корнями кратности характеристического уравнения. В этих особых случаях частное решение отличается от правой части уравнения не только постоянными коэффициентами, то и дополнительным множителем .

Для решения неоднородного дифференциального уравнения малого порядка можно использовать метод Лагранжа (метод вариации произвольных постоянных). Пусть и  -- независимые частные решения уравнения . Тогда решение уравнения по методу Лагранжа находится в виде , где и  -- функции от , удовлетворяющие системе дифференциальных уравнений:

Следовательно,

Решив полученные обыкновенные дифференциальные уравнения первого порядка, получим и общее решение исходного дифференциального уравнения.

24. МЕТОД ПОДБОРА ПОСТРОЕНИЯ ЧАСТНОГО РЕШЕНИЯ ЛИНЕЙНОГО НЕОДНОРОДНОГО УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ. Рассмотрим линейное неоднородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1y^{(n - 1)} + ... + a₁y' + a₀y = f(x).

Коэффициенты a_n-1, ... , a₁, a₀ — постоянные десйствительные числа, f(x) — непрерывная на [a, b] правая часть.

Общее решение этого уравнения имеет вид y(x) = C₁y₁(x) + C₂y₂(x) + ... + C_ny_n(x) + y*(x),

где С₁, С₂, ..., С_n — произвольные постоянные, y₁(x), y₂(x), ..., y_n(x) — фундаментальная система решений однородного уравнения, y*(x) — частное решение неоднородного уравнения.

 

Частное решение y*(x) можно найти методом подбора, если правая часть уравнения — квазимногочлен — функция вида

f(x) = exp(αx)(M_m(x)cos(βx) + N_n(x)sin(βx)).

Здесь M_m(x) — многочлен степени m, N_n(x) — многочлен степени n, α и β — действительные числа.

Метод подбора вычисления частного решения линейного неоднородного уравнения с квазимногочленом в правой части состоит в том, что частное решение уравнения

отыскивают в виде

y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx))x^r,

где P_k(x) и Q_k(x) — многочлены степени k = max(n, m) с неизвестными коэффициентами,

P_k(x) = p_kx^k + p_k-1x^k-1 + ... + p₁x + p₀, Q_k(x) = q_kx^k + q_k-1x^k-1 + ... + q₁x + q₀.

Для того чтобы найти неизвестные коэффициенты многочленов P_k(x) и Q_k(x) , подставляем y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx)) в уравнение и приравниваем в правой и левой части полученного равенства коэффициенты при

exp(αx)cos(βx), exp(αx)sin(βx), xexp(αx)cos(βx), xexp(αx)sin(βx),  x²exp(αx)cos(βx), x²exp(αx)sin(βx), ...,   x^kexp(αx)cos(βx), x^kexp(αx)sin(βx).

Полученная таким образом система 2k + 2 уравнений относительно 2k + 2 неизвестных имеет единственное решение.

 

Метод подбора применяется к ограниченному, но достаточно широкому классу правых частей, поскольку квазимногочленами являются функции вида:

M_k(x),  M_k(x)exp(αx),  M_k(x)cos(βx),   M_k(x)sin(βx),  exp(αx)(M_m(x)cos(βx) + N_n(x)sin(βx)).  

25.Нормальная система дифференциальных уравнений. При рассмотрении систем дифференциальных уравнений ограничимся случаем системы трех уравнений (n = 3). Все нижесказанное справедливо для систем произвольного порядка.

Определение. Нормальная система дифференциальных уравнений c постоянными коэффициентами называется линейной однородной, если ее можно записать в виде:

   (2)

  Решения системы (2) обладают следующими свойствами:

1) Если y, z, u – решения системы, то Cy, Cz, Cu , где C = const – тоже являются решениями этой системы.

2) Если y₁, z₁, u₁ и y₂, z₂, u₂ – решения системы, то y₁ + y₂, z₁ + z₂, u₁ + u₂ – тоже являются решениями системы.

  Решения системы ищутся в виде:

Подставляя эти значения в систему (2) и перенеся все члены в одну сторону и сократив на e^kx, получаем:

Для того, чтобы полученная система имела ненулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.:

 В результате вычисления определителя получаем уравнение третьей степени относительно k. Это уравнение называется характеристическим уравнением и имеет три корня k₁, k₂, k₃. Каждому из этих корней соответствует ненулевое решение системы (2):

 Линейная комбинация этих решений с произвольными коэффициентами будет решением системы (2):

26. Системы ДУ с постоянными коэффициентами. Система уравнений вида

                                               ,                                                               (1)

называется неоднородной системой линейных дифференциальных уравнений с постоянными коэффициентами. Будем считать, что   являются непрерывными функциями на (a,b).

Система дифференциальных уравнений

                                                 ,                                                                      (2)

называется однородной. Вводя в рассмотрение векторы и матрицу , уравнения (1),(2) можно представить в векторной форме

                                                                      ,                                                                      (1')

                                                                      .                                                                          (2')

Матрица

                                                         ,                                                              (3)

где - координаты линейно независимых решений (векторов)

...........................

векторного уравнения (2'), называется фундаментальной матрицей этого уравнения. Иногда ее называют матрицей Вронского.

Определитель

,

составленный из частных решений системы (2), называется определителем Вронского. Для того, чтобы матрица (3), где - частные решения системы уравнений (2), была фундаментальной, необходимо и достаточно, чтобы при . При этом общее решение векторного уравнения (2') представляется в виде

,

где C - произвольный постоянный вектор. Общее же решение уравнения (1') будет

,

где - какой-нибудь вектор, являющийся частным решением уравнения (1').

Путем исключения неизвестных систему всегда можно свести к уравнению более высокого порядка с одной неизвестной функцией. Этот метод удобен для решений несложных систем.

27. Метод Эйлера. Если задачу об отыскании решений дифференциального уравнения удаётся свести к конечному числу алгебраических операций, операций дифференцирования и интегрирования известных функций, то говорят, что дифференциальное уравнение интегрируется в квадратурах.

В приложениях крайне редко встречаются уравнения. интегрируемые в квадратурах. Для исследования и решения уравнений, которые не интегрируются в квадратурах, используются численные методы решения задачи Коши.

 

Численное решение задачи Коши y' = f(x, y), y(a) = y₀ на отрезке [a, b] состоит в построении таблицы приближённых значений y₀, y₁, ..., y_i, ..., y_N решения y = y(x), y(x_i) ≈ y_i ,

в узлах сетки a = x₀< x₁< ...< x_i< ...< x_N = b. Если x_i = a + ih, h = (b-a)/N, то сетка называется равномерной.

 

Численный метод решения задачи Коши называется одношаговым, если для вычисления решения в точке x₀ + h используется информация о решении только в точке x₀.

Простейший одношаговый метод численного решения задачи Коши — метод Эйлера.  В методе Эйлера величины y_i вычисляются по формуле: y_i+1 = y_{i + h·f(xi, yi):}

_{y' = f(x, y),  y(a) = y0 , x ∈ [a, b],}

_{xi = a + ih, h = (b-a)/N, i = 0,1 , 2, ..., N,}  

_{y(xi)≈ yi ,}

_{yi+1 = yi + h·f(xi, yi).}

_{Для погрешности метода Эйлера на одном шаге справедлива оценка}

_{а для оценки погрешности решения на всём отрезке [a, b] справедливо}

_{Для практической оценки погрешности можно рекомендовать правило Рунге:производятся вычисления с шагом h — вычисляютcя значения y}^(h)_{i, затем производятся вычисления с половинным шагом h/2 — вычисляютcя значения y}^(h/2)_{i .}

 

_{За оценку погрешности вычислений с шагом h/2 принимают величину}

 

_{Если соединить точки (xi, yi) прямолинейными отрезками, получим ломаную Эйлера — ломаную линию, каждое звено которой с началом в точке (xi, yi) имеет угловой коэффициент, равный f(xi, yi).}

35. Формула Грина. Пусть в плоскости Oxy задана область R, ограниченная замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некоторой области, содержащей R, задана непрерывная векторная функция

с непрерывными частными производными первого порядка . Тогда справедлива формула Грина

где символ указывает, что кривая (контур) C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки. Если , то формула Грина принимает вид

где S − это площадь области R, ограниченной контуром C. Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля. Пусть векторное поле описывается функцией

Ротором или вихрем векторного поля называется вектор, обозначаемый или и равный

Формула Грина в векторной форме записывается в виде

Заметим, что формула Грина вытекает из "теоремы Стокса" при переходе от трехмерного случая к случаю двух координат.

37.Формула Остроградского-ГауссаОбозначим через G трехмерное тело, ограниченное кусочно-непрерывной, гладкой, замкнутой поверхностью S с внешней нормалью. Предположим, что задано векторное поле

компоненты которого имеют непрерывные частные производные. Согласно формуле Остроградского-Гаусса,

где через

обозначена дивергенция векторного поля (она обозначается также символом ). Символ указывает, что поверхностный интеграл вычисляется по замкнутой поверхности. Формула Остроградского-Гаусса связывает поверхностные интегралы второго рода с соответствующими тройными интегралами. Данную формулу можно записать также в координатной форме:

В частном случае, полагая , получаем формулу для вычисления объема тела G:

36.Формула Стокса. Пусть S является гладкой поверхностью, ограниченной гладкой кривой C. Тогда для любой непрерывно дифференцируемой векторной функции

справедлива теорема Стокса:

где

− ротор векторного поля . Символ показывает, что криволинейный интеграл вычисляется по замкнутой кривой. Будем предполагать, что ориентация поверхности и направление обхода кривой соответствуют правилу правой руки. В этом случае при обходе кривой поверхность всегда остается слева, если голова направлена в ту же сторону, что и вектор нормали (рисунок 1). Теорема Стокса связывает между собой криволинейные интегралы второго рода и поверхностные интегралы второго рода. В координатной форме теорема Стокса может быть записана в следующем виде:

32.Двойной интеграл в полярных координатах. Одним из частных случаев замены переменных является переход из декартовой в полярную систему координат (рисунок 1).

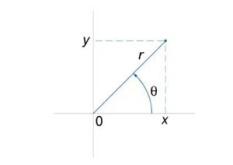
Якобиан такого преобразования имеет вид

Следовательно, дифференциальный элемент в полярных координатах будет равен

Пусть область интегрирования R в полярных координатах определяется следующим образом (рисунок 2):

Тогда двойной интеграл в полярных координатах описывается формулой

Будем называть полярным прямоугольником область интегрирования, показанную на рисунке 3 и удовлетворяющую условиям

В этом случае формула замены переменных в двойном интеграле имеет вид

31.Замена переменной в двойном интеграле. Для вычисления двойного интеграла иногда удобнее перейти в другую систему координат. Это может быть обусловлено формой области интегрирования или сложностью подынтегральной функции. В новой системе координат вычисление двойного интеграла значительно упрощается. Замена переменных в двойном интеграле описывается формулой

где выражение представляет собой так называемый якобиан преобразования , а S − образ области интегрирования R, который можно найти с помощью подстановки в определение области R. Отметим, что в приведенной выше формуле означает абсолютное значение соответствующего определителя. Предполагая, что преобразование координат является взаимно-однозначным, обратное соотношение описывается якобианом

при условии, что знаменатель нигде не равен 0. Итак, замена переменных в двойном интеграле производится с помощью следующих трех шагов:

1.Найти образ S в новой системе координат для исходной области интегрирования R;

2.Вычислить якобиан преобразования и записать дифференциал в новых переменных Заменить в подынтегральном выражении исходные переменные x и y, выполнив, соответственно, подстановки и .