Встроенные функции

MathCAD содержит большое число встроенных функций, используемых при описании процессов, происходящих в объектах электротехники и энергетики. Любые функции, используемые в высшей школе, поддерживает MathCAD. Это элементарные тригонометрические, гиперболические, векторные и матричные и др. Примеры абстрактного пользования встроенными функциями приведены на рис. 5.

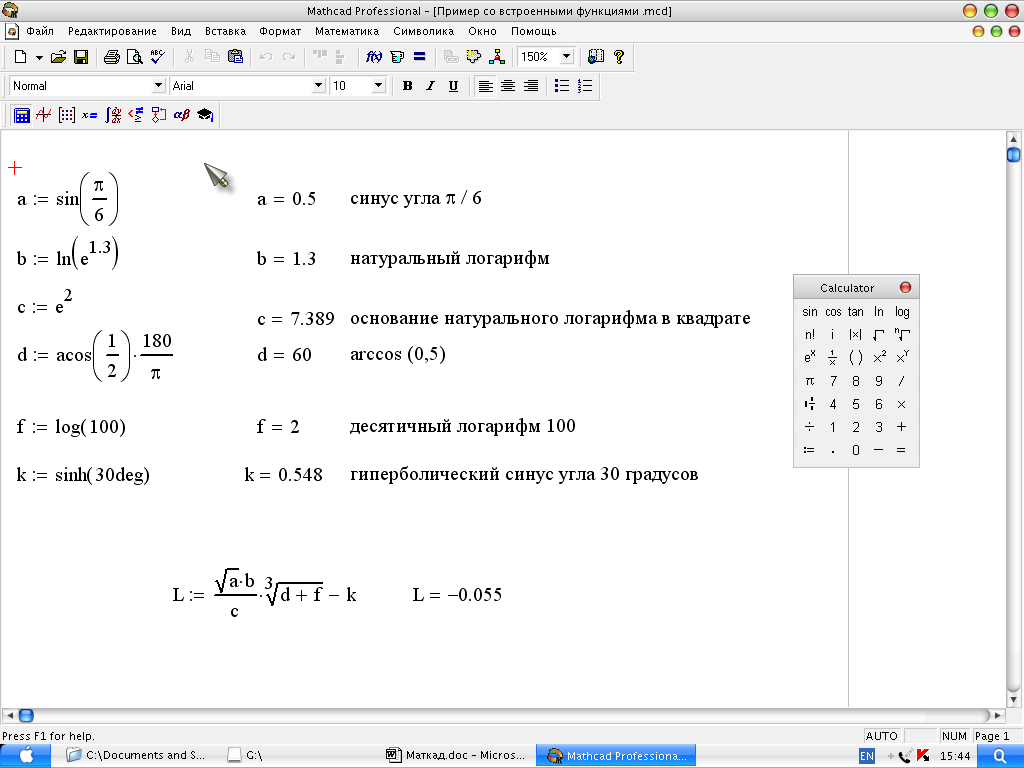
Рис.5. Пример программы с использованием встроенных функций.

Решение систем линейных уравнений

Требуется решить систему уравнений третьего порядка:

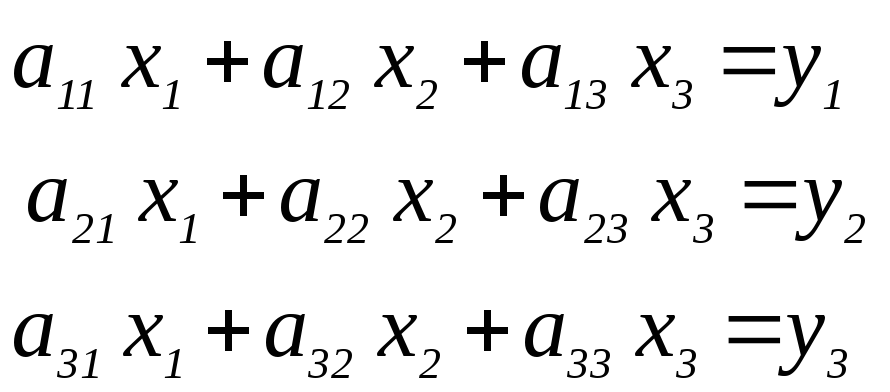
В MathCAD система уравнений решается как , где – квадратная матрица коэффициентов системы линейных уравнений; – матрица-вектор свободных членов. Пример решения приведен на рис 6.

Решить задачу можно тремя способами. Во всех трех необходимо заполнить матрицы соответствующими членами. Присвоение переменной матрицы осуществляется через меню Matrix. Нажатием кнопки в верхнем левом углу выводится панель Вставить матрицу. По умолчанию количество строк и узлов матрицы равно трем. Порядок системы уравнений примера также равен трем, поэтому нажимаем кнопку ОК. Присваиваем переменной вектор столбец через ту же кнопку. Но на панели Вставить матрицу количество столбцов задаем 1. Далее решаем уравнение .

По первому способу матрицы и заполняются непосредственно численными значениями коэффициентов. Результат выводится в виде матрицы-вектора. Индексы в системе MathCAD начинаются с нулевого номера. Т.е., первое неизвестное в полученном результате имеет нулевой индекс, – первый, – второй.

По второму способу сначала присваиваются значения коэффициентов матриц, которые затем заносятся в матрицы.

По третьему способу присвоение производится непосредственно коэффициентам матриц.

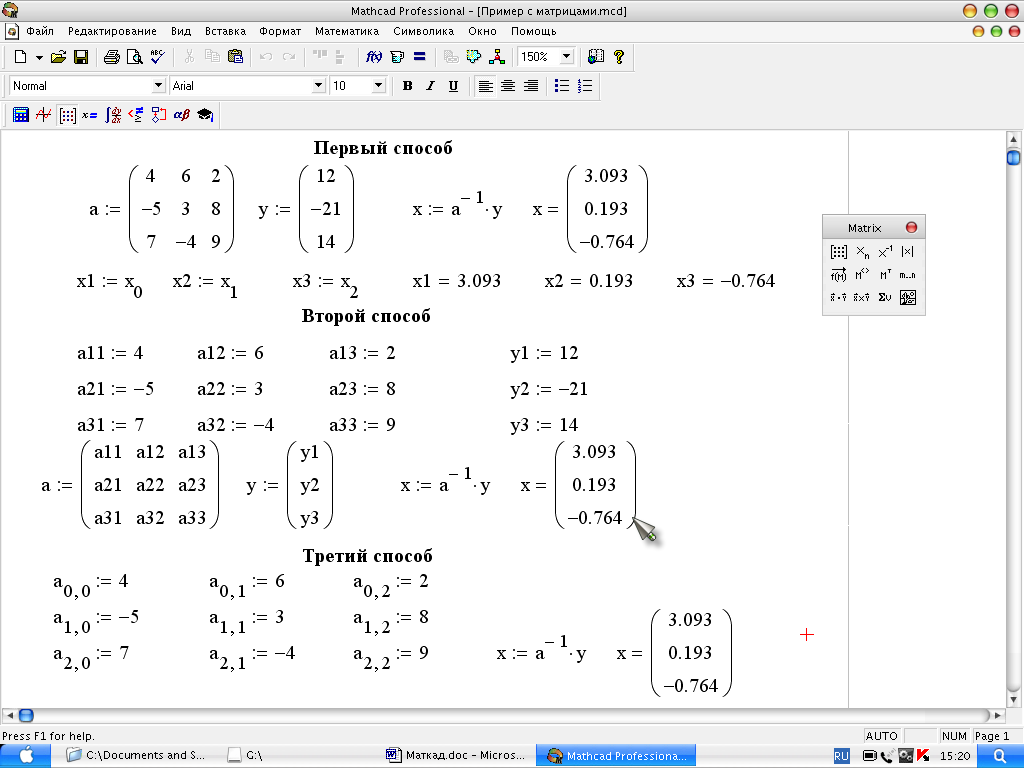Рис. 6. Примеры решения системы линейных уравнений.

Нетрудно убедиться, что результат вычислений один и тот же. Каждый способ имеет свои достоинства и недостатки. Применение их диктуется в зависимости от решаемой задачи. При разборе примеров решения задач электротехники мы будем обосновывать применение того или иного способа.

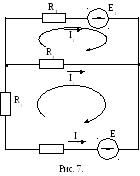
Рассмотрим пример применения данного алгоритма к определению токов на основании законов Кирхгофа в цепи, изображенной на рис. 7.

Уравнения, описывающие процессы в цепи, следующие:

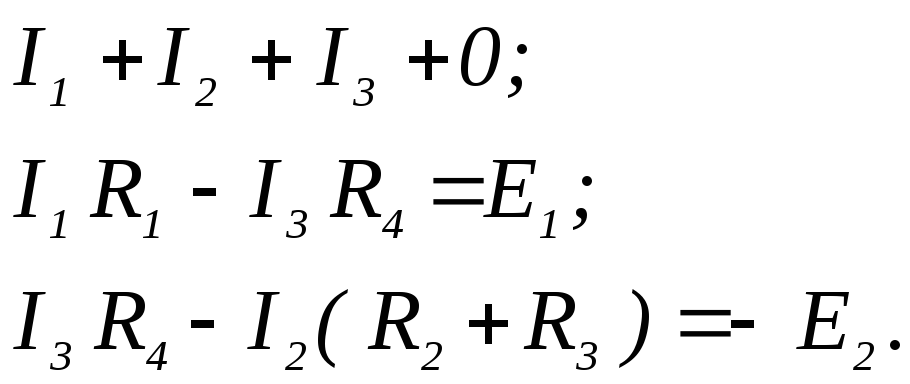
Программа расчета токов приведена на рис. 8.

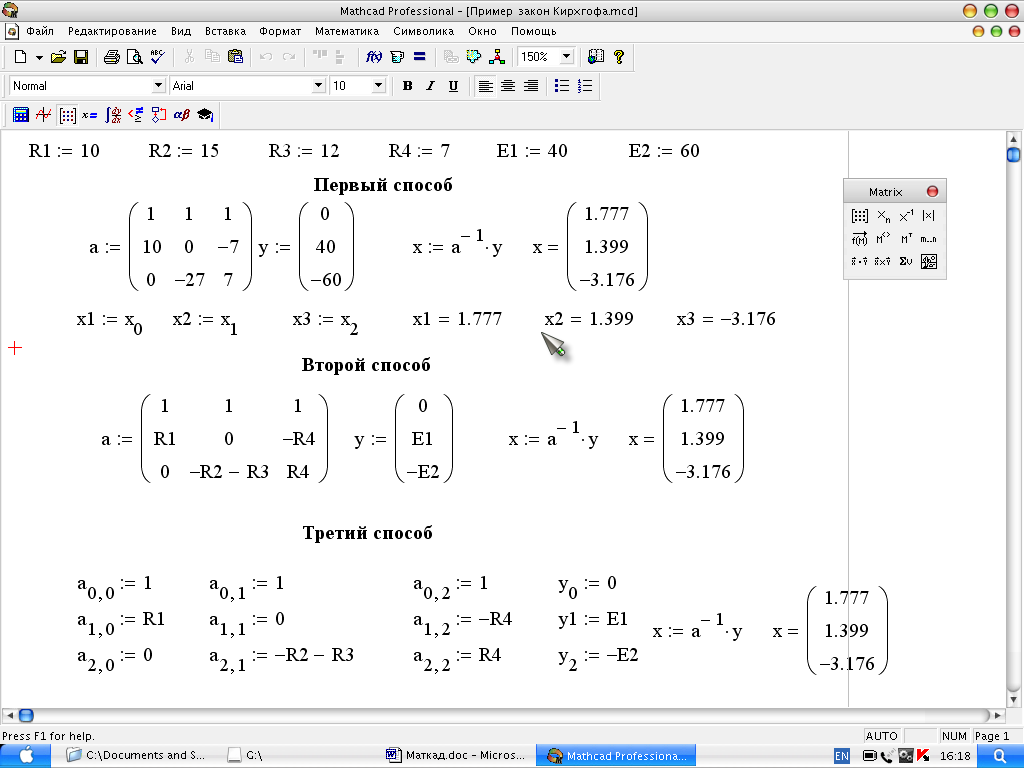
Рис 8. Варианты программ расчета токов цепи рис. 7.

В первом варианте коэффициенты матриц вычисляются предварительно. Опыт показывает, что это может привести к ошибкам. Этот вариант уместен, если коэффициенты матриц вычислять предварительно не надо. Во втором варианте вероятность ошибок меньше, и очень удобно проверять уравнения.

Вариант с заданием коэффициентов с использование индексов очевидно более трудоемок. Он, как будет показано ниже, является единственным при большом числе неизвестных.

Никогда не выполняйте ту работу, которую компьютер выполнит лучше!

В некоторых учебниках по Теоретическим основам электротехники токи в ветвях рекомендуется рассчитывать через определители матриц. В системе MathCAD определитель выполняется оператором |x| из меню Calculator или Matrix. Пример программы приведен на рис. 9. Результаты расчета, естественно, совпадают с расчетами, выполненными через обратную матрицу .

В программах, приведенных на рис. 8 и 9, нет комментариев. Все идентификаторы соответствуют общепринятым обозначениям в теории электрических цепей. Авторы считают, что пользователь достаточно хорошо изучил соответствующие разделы Теоретических основ электротехники.

Р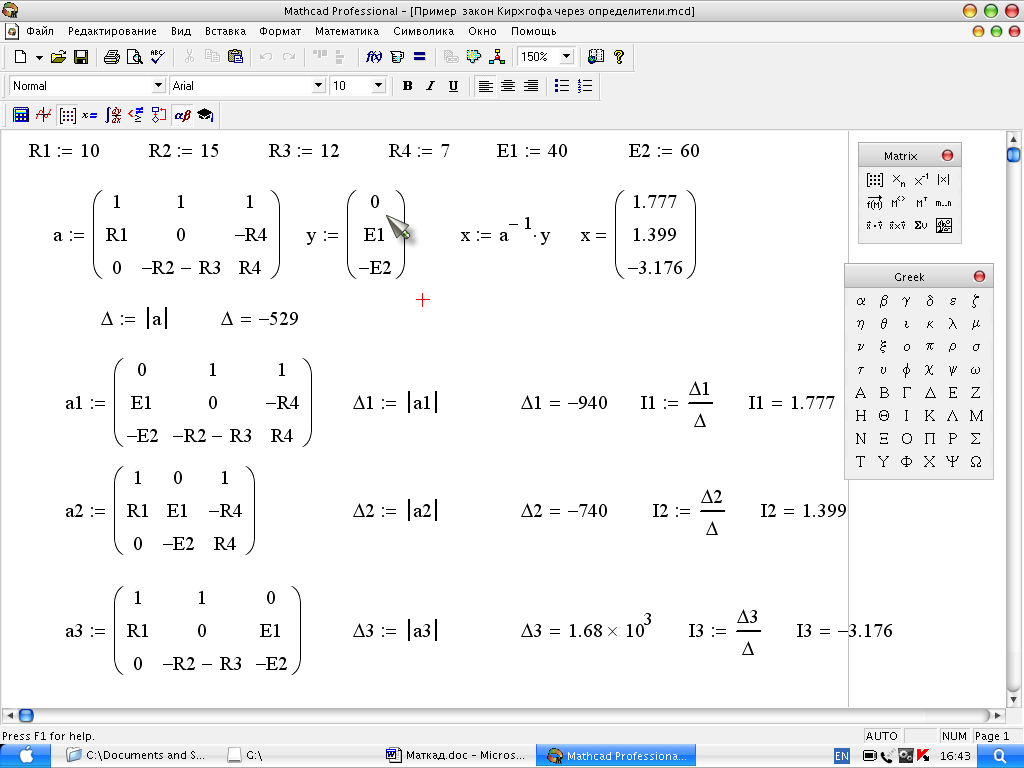 ис. 9. Пример программы расчета токов рис. 7. через определители.

При числе неизвестных токов или напряжений до 4 - 5 в рассчитываемой цепи целесообразно заполнение матрицы выполнять непосредственно, но в идентификаторах, как это выполнено при решении задачи на рис 8 вторым способом. Это уменьшит вероятность ошибок и облегчит проверку правильности составления уравнений.

Если неизвестные в системе уравнений в целочисленной степени, можно воспользоваться ключевым словом Given. Однако пользоваться этим приемом следует осторожно. Система уравнений решается итерационными методами. Поэтому очень важным является первое приближение. Когда решается одно уравнение с неизвестным в первой степени, величина первого приближения практически несущественна. Но, когда какой-либо корень имеет несколько значений, от величины и вида первого приближения зависит решение. Может оказаться, что MathCAD с задачей не справится.

Ниже приводятся несколько примеров решения систем уравнений (рис. 10).

Для решения системы уравнений необходимо выполнить следующее:

• для всех неизвестных, входящих в систему уравнений задаются начальные приближения;

• печатается ключевое слово Given. Оно указывает MathCAD, что далее следует система уравнений. При печати слова Given можно использовать любой шрифт, прописные или строчные буквы;

• вводится уравнения и неравенства в любом порядке ниже ключевого слова Given. Между правыми и левыми частями уравнения должен стоять знак равенства из палитры Boolean. Можно напечатать этот знак одновременным нажатием клавиш Ctrl и = .

• вводится любое выражение, включающее функцию Find. При печати слова Find можно использовать любой шрифт, прописные или строчные буквы.

Рис. 10. Примеры решения уравнений

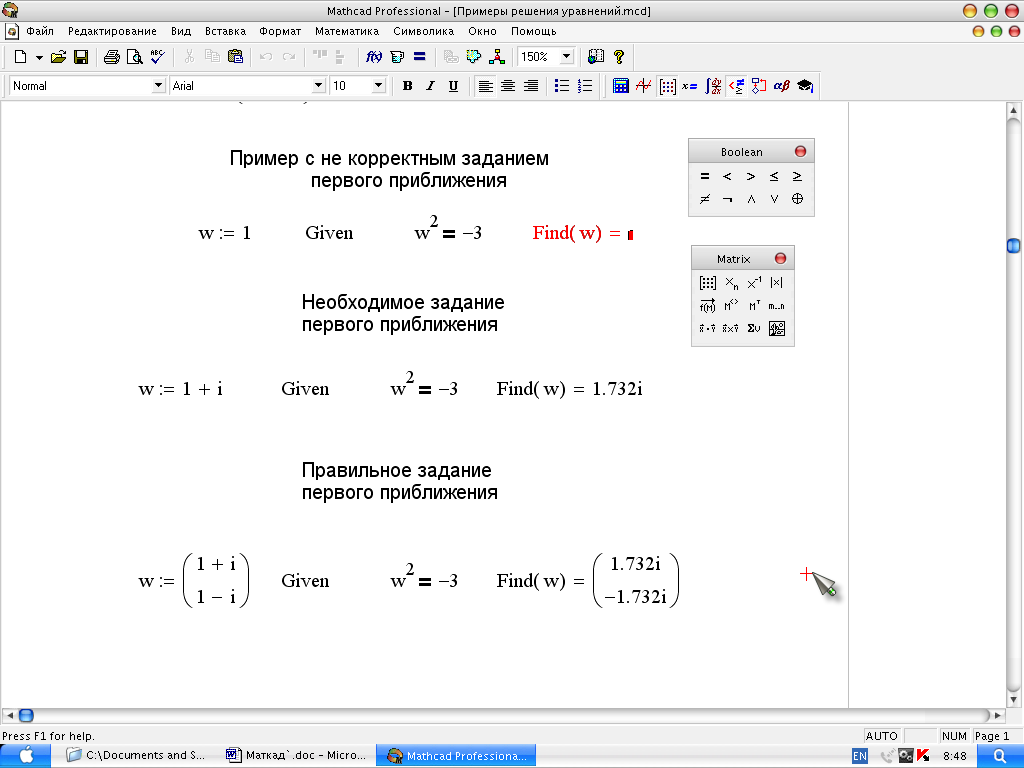
Рис. 10а. Примеры решения уравнений

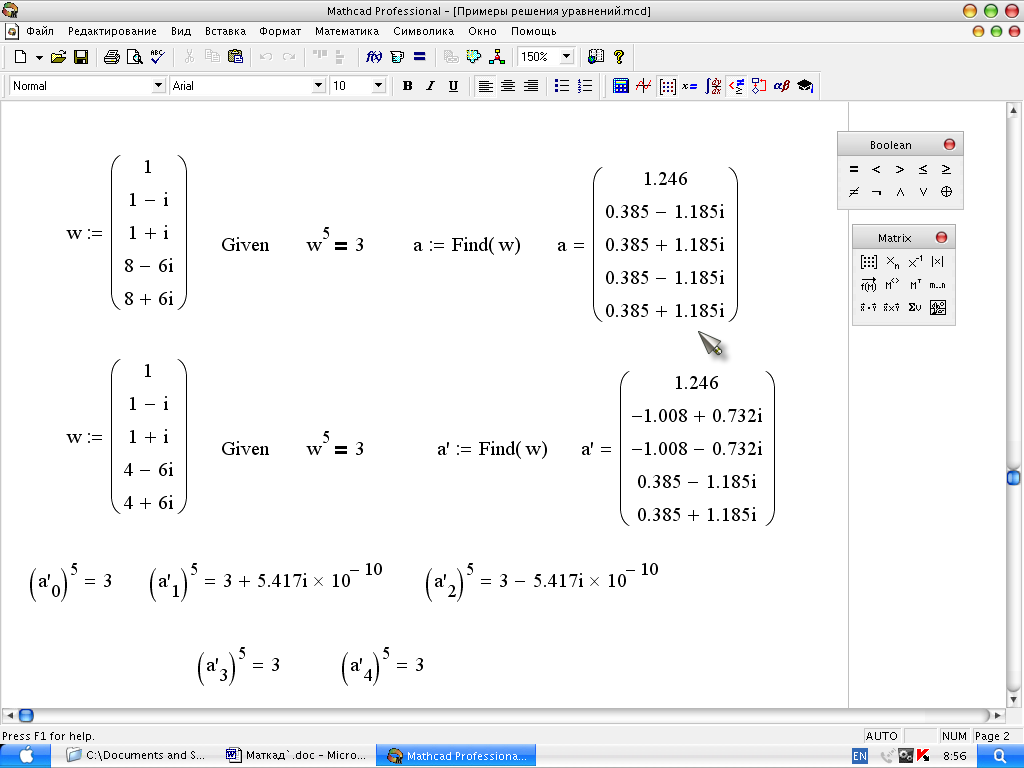
Рис. 10б. Примеры решения уравнений

На рис. 10 второй пример показывает, как решить систему уравнений с неизвестными во второй степени. Поскольку для каждого неизвестного задано только по одному приближению, решение выполнено для одного корня каждого неизвестного. Чтобы получить вторые корни, необходимо задаться новыми приближениями, которые находятся ближе ко вторым корням, чем первые. Хорошо, если известно в какой области искать корни. Но в большинстве случаев это не известно, и задача очень усложняется.

Существенно также, в области действительных или мнимых чисел находятся корни уравнения. Если корни мнимые, а первое приближение задано как действительное число, то решение найдено не будет. Поэтому в общем случае надо первое приближение надо задавать комплексным числом. А если корней несколько, то и приближений должно задаваться столько же. Пример решения одного уравнения второй степени приведен на рис. 1.7а.

Влияние первого приближения на истинность решения иллюстрируется примером, приведенным на рис. 10в, где решается уравнение пятой степени. В первом примере два корня уравнения повторились. И только после изменения первого приближения получены все корни. Проверка правильности корней, приведенная там же, показала, что корни найдены правильно.