1.10. Ортогональное дополнение

Определение 1.16 Пусть - подпространство евклидова пространства .

Ортогональным дополнением подпространства называется такое множество векторов , что .

Утверждение 1.11 Ортогональное дополнение есть подпространство (каково бы ни было подпространство ).

Доказательство. Из свойств скалярного умножения ясно, что для любых (каков бы ни был вектор ). Тем самым вместе с любыми двумя векторами ортогональное дополнение содержит их сумму. Аналогично - для умножения на число.

Утверждение 1.12 Для любых ненулевых векторов и .

Доказательство очевидно.

Утверждение 1.13

Доказательство. Предположим, что существует ненулевой вектор . Тогда должно быть , что невозможно.

Утверждение 1.14

Утверждение 1.15 .

Доказательство 1.14 и 1.15 очевидно.

Пусть теперь в подпространстве задан ортонормированный базис . Введем также ортонормированный базис во всем пространстве : , и пусть - обычное разложение системы по базису . Тогда, если вектор , то тогда и только тогда, когда столбец есть решение однородной системы

(1)

(действительно, каждый столбец матрицы есть столбец координат соответствующего вектора базиса в базисе , а при скалярном перемножении векторов , заданных разложениями в ортонормированном базисе .

Размерность пространства решений системы (1) равна . Значит,

(2)

Тем самым мы доказали, что имеет место разложение произвольного конечномерного евклидова пространства в виде объединения некоторого его подпространства и его ортогонального дополнения:

, причем

подпространства и не имеют общих точек, кроме нулевого вектора, и выполняется соотношение размерностей (2).

Такое разложение евклидова пространства называется разложением в прямую сумму двух подпространств, каждое из которых служит ортогональным дополнением другого. Это записывают в виде:

Например,

,

т.е., пространство геометрических векторов раскладывается в прямую сумму подпространства всех векторов, параллельных плоскости , и всех векторов, параллельных оси аппликат.

Более общо, если в пространстве фиксировать некоторую плоскость , то пространство геометрических векторов раскладывается в прямую сумму:

,

где - подпространство всех векторов, параллельных плоскости , а - подпространство всех векторов, параллельных прямой .

1.11. Собственные векторы и собственные числа линейного оператора.

Везде в дальнейшем изложении, если только специально не оговорено противное, под термином линейный оператор понимается линейное преобразование некоторого конечномерного линейного пространства .

Определение 1.17 Ненулевой вектор называется собственным вектором линейного оператора , если существует такое вещественное число, что . Число называется при этом собственным числом, или собственным значением оператора .

Собственный вектор называется в этом случае собственным вектором, принадлежащим собственному числу .

Заметим, что собственное число может быть равно нулю.

Утверждение 1.16 Один и тот же собственный вектор не может принадлежать одновременно двум разным собственным числам.

Доказательство. Пусть , но . Тогда , откуда, так как , в противоречии с допущением.

Но одному и тому же собственному числу может принадлежать много собственных векторов. Более того, множество

всех собственных векторов оператора , принадлежащих данному собственному числу , образует подпространство пространства .

В самом деле:

,

каковы бы ни были собственные векторы , принадлежащие собственному числу , и вещественные числа .

Размерность подпространства называется геометрической кратностью собственного числа . Само же это подпространство называется собственным подпространством, принадлежащим собственному числу .

Рассмотрим задачу об отыскании собственных векторов и собственных чисел линейного оператора.

Имеем:

,

где - тождественный оператор.

Тогда из равенства

следует

(1)

(см. п. 1.8).

Задавая произвольно некий базис , получим из (1) следующее матричное уравнение:

, (2)

где - матрица в базисе , и .

Рассматривая (2) как однородную систему относительно столбца , получим (первый семестр!), что для того, чтобы эта система имела ненулевые решения, необходимо и достаточно, чтобы

(3)

Используя понятие детерминанта линейного оператора (п. 1.9), мы можем переписать (3) в виде:

(4)

Уравнение (4) называется характеристическим уравнением оператора , а его корни - характеристическими числами данного оператора. Множество всех характеристических чисел оператора образует его спектр. Из предыдущего совершенно ясно, что характеристическое уравнение и спектр линейного оператора не зависят от выбора конкретного базиса, являются, как говорят, инвариантами. Подчеркнем, что корни характеристического уравнения могут быть комплексными. Сам детерминант, образующий левую часть характеристического уравнения, является, как нетрудно понять, многочленом -ой степени от и называется характеристическим многочленом (полиномом) данного оператора. Собственные числа оператора - это в точности все вещественные характеристические числа. Существует один важный класс линейных операторов - самосопряженные операторы ,- который мы изучим позже, когда весь спектр оператора лежит в вещественной области. Тогда понятия характеристического и собственного числа совпадают.

В общем же случае для того, чтобы найти собственные числа и собственные векторы данного линейного оператора, следует поступать так:

1) составить и решить характеристическое уравнение, выбрав произвольный базис (обычно это канонический базис соответствующего арифметического пространства);

2) для каждого вещественного корня характеристического уравнения решить однородную систему (2); фундаментальные решения этой системы и образуют базис подпространства (точнее, конечно, они образуют базис арифметического пространства, изоморфного подпространству , но мы будем часто отождествлять конечномерное линейное пространство с изоморфным ему пространством арифметических векторов) , а общее решение системы определяет множество всех собственных векторов, принадлежащих .

Примеры. 1) Определим в оператор матрицей (по умолчанию предполагается выбранным канонический базис):

.

Характеристическое уравнение будет иметь вид:

,

или

,

откуда

Таким образом данный оператор не имеет ни одного вещественного характеристического числа и, следовательно, ни одного собственного вектора в пространстве .

2. Пусть в 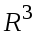оператор определяется матрицей:

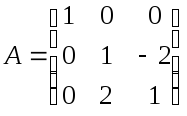
Характеристическое уравнение:

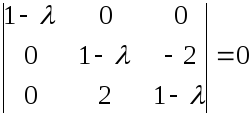
Раскрывая определитель, получим:

,

откуда (см. предыдущий пример):

.

Здесь, в спектре оператора, есть одно вещественное число, и мы можем определить множество собственных векторов, принадлежащих этому числу. Для этого нужно решить однородную систему с матрицей

Ясно, что решение такой системы будет:

(где - произвольная константа), или

3) Решим задачу о собственных числах и собственных векторах оператора проектирования, определенного в п. 1.7.

В базисе матрица этого оператора, рассматриваемого как преобразование пространства геометрических векторов, имеет вид:

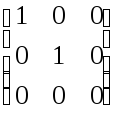
Характеристическое уравнение:

.

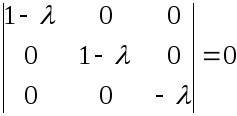
В данном случае все характеристические числа оказались вещественными.

Определяем собственные векторы:

1)

Однородная система с такой матрицей будет иметь общее решение

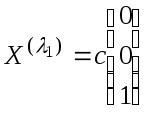
Геометрически собственное подпространство, принадлежащее данному собственному числу, есть множество всех векторов, параллельных оси аппликат:

2. 

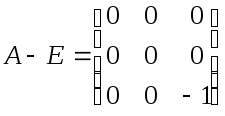
Однородная система с такой матрицей имеет общее решение:

,

где - произвольные вещественные константы. Геометрически, как легко понять, это множество всех векторов, лежащих в плоскости . Обратим внимание на то, что размерность собственного подпространства, принадлежащего собственному числу 1, равна двум и совпадает с кратностью данного характеристического корня как корня многочлена. Позже мы увидим, что такое совпадение не случайно.

В заключение этого пункта докажем одну важную теорему.

Теорема 1.6 Собственные векторы, принадлежащие попарно различным собственным числам данного линейного оператора, линейно независимы.

Доказательство. Пусть - попарно различные собственные числа некоторого линейного оператора .

Будем доказывать утверждение теоремы индукцией по .

Для утверждение тривиально, так как система, состоящая из одного ненулевого вектора, линейно независима.

Пусть утверждение доказано для всех . Рассмотрим множество попарно различных собственных чисел . Пусть - собственные векторы, принадлежащие числам соответственно. Предположим, что они линейно зависимы. Тогда найдется нетривиальная линейная комбинация этих векторов, обращающаяся в нуль:

(5)

Подействуем оператором на обе части равенства (5), получим:

.

Так как - собственные векторы оператора , то

(6)

Умножив равенство (5) на , вычтем его из (6):

(7)

Последнее равенство (7) есть утверждение о равенстве нулю линейной комбинации линейно независимой системы. Такая линейная комбинация может быть только тривиальной, т.е.

Так как разность в скобках, ввиду того, что все рассматриваемые собственные числа попарно различны, не равна нулю, то все числа равны нулю. С учетом этого равенство (5) принимает вид:

,

но поскольку , остается признать, что и, следовательно, линейная комбинация в (5) тривиальна в противоречии с предположением.

Это значит, что векторы линейно независимы.

Теорема доказана.