§ 3.6 Пересчет координат вектора при смене базиса

Теорема 1. Пусть известно разложение вектора х в базисе , т.е. известны числа , что

.

Рассмотрим вектор z. Пусть известны числа , что

.

Тогда система векторов , где вектор z заменяет вектор е_i, будет базисом.

Доказательство. Напомним, система векторов будет базисом, если определитель матрицы координат будет отличен от нуля.

Так как система образует базис, то матрица ее координат отлична от нуля. Если мы меняем вектор е_i на z, то в матрице координат появится столбец, состоящий из суммы координат системы векторов . Используя свойство определителя – о представлении элементов некоторого столбца в виде суммы слагаемых - приходим к нужному результату.

Теорема 2. Пусть известно разложение вектора х в базисе , т.е.

.

Рассмотрим некоторый вектор z и его разложение в этом базисе

.

Тогда в базисе координаты вектора определяются по формуле:

, d_j = x_j - d_iz_j (1)

Доказательство.

Приравняем по вектору х оба его разложения в разных базисах. Тогда, с условием разложения вектора z, получим цепочку равенств

Приравнивая коэффициенты при векторах , получим требуемые формулы

, d_j = x_j - d_iz_j

Пример.

1. Пусть задан базис 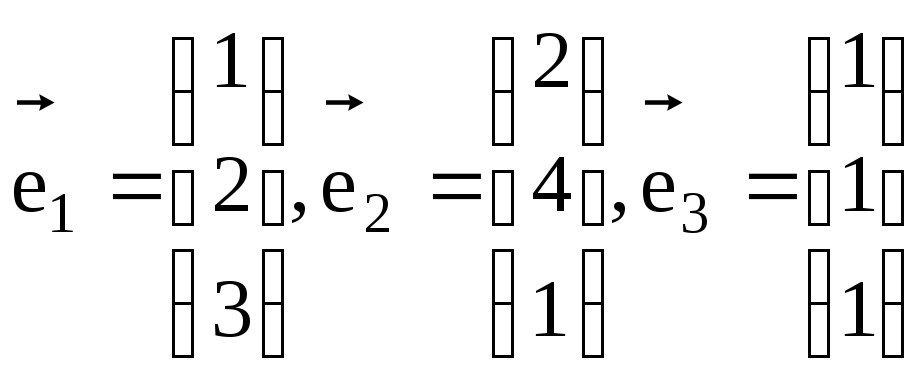и известно разложение

вектора 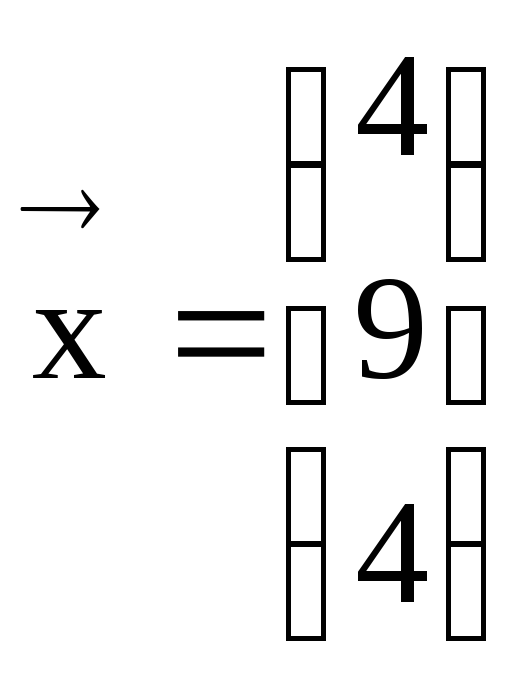по базису: 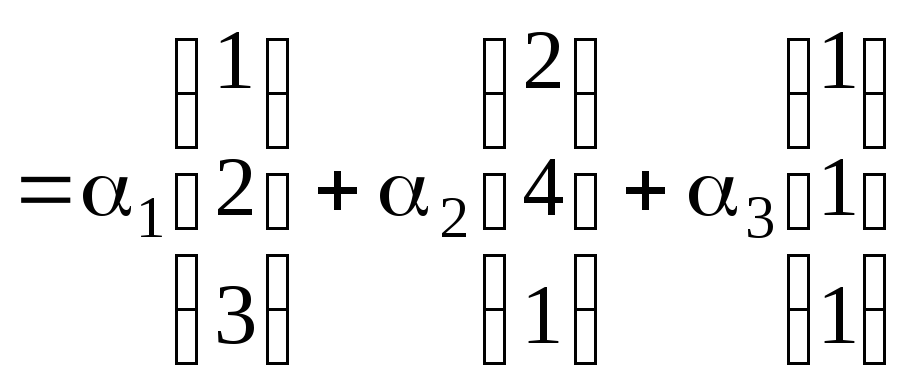,где коэффициенты

разложения имеют значения: ₁=1,₂=2,₃=-1

Пусть разложение вектора z этом базисе: z=.

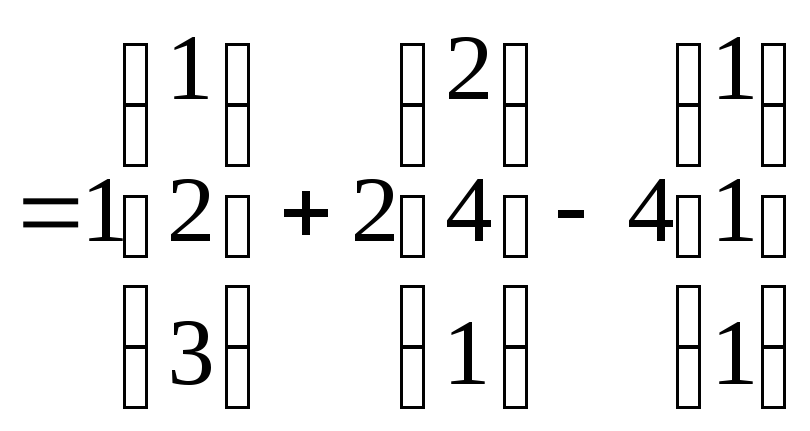Найдем координаты d₁, d₂, d₃ разложения вектора х в новом базисе {е₁ , z, е₃ }, где вместо вектора е₂ введен вектор z .

Решение. Согласно полученным формулам (1):

1, d₁=x₁ - d₂z₁ =1 – 1=0, d₃ =x₃ - d₂z₃ = -1+4=3

Проверим полученный результат:

х = d₁ e₁ + d₂ z + d₃ e₃ = 1 + 3 =

§ 3.7 Векторное и смешанное произведение векторов.

Будем говорить, что вектора (a, b, c) в геометрическом пространстве R³ , где определено скалярное произведение, образуют правую тройку, если кратчайший поворот вектора a к вектору b, зафиксированный из точки, расположенной в вершине вектора с, совершается против часовой стрелки. Если указанный поворот совершается по часовой стрелке, то тройка a, b, c называется левой.

c c

b b

a a

Правая тройка a, b, c Левая тройка a, b, c

Определение 1. Векторным произведением двух векторов a, b в пространстве R³ с ортонормированным базисом е₁, е_2, е₃, называется третий вектор c, удовлетворяющий условиям:

1. Вектор с перпендикулярен каждому из векторов а и b

2. Длина вектора с равна произведению длин векторов а и b на синус угла между ними, т.е.

с = аbsin(ab) (1)

3. Тройки векторов {а, b, c} и {е₁, е_2, е₃} имеют одинаковую ориентацию (обе правые или левые).

Векторное произведение записывают в виде

с=ахb или с=[аb] (2)

Из формулы (1) следует, что модуль (длина) вектора с равна площади S параллелограмма, построенного на векторах a, b или

S = [а b] (3)

Комментарии к определению.

1. Условия 1-3 определяют вектор [а b] для любой пары а,b однозначно

2. При замене базиса {е₁, е_2, е₃} другим базисом с противоположной ориентацией вектор с заменяется на вектор –с

3. При вычислении векторного произведения удобна следующая формула: если векторы а и b заданы своими координатами

а =(а₁,а₂,а₃), b =(b₁, b₂, b₃), то

е₁ е_2, е₃ a₂a₃ a₃a₁ a₁ a₂

[a x b]= a₁ а₂ а₃ = е₁ + е₂ + е₃ = ₁е₁+ ₂е₂ + ₃е₃ (4)

b₁ b₂ b₃ b₂b₃ b₃b₁ b₁ b₂

Тогда, площадь параллелограмма будет равна:

S = [axb] = (5)

Если задан ортонормированный базис E =(e₁, e₂, e₃), то их векторные произведения

(e₁ х e₁) = 0, (e₁ х e₂) = e₃, (e₂ х e₃)= e₁, (e₁ х e₃)= e₂

Основные свойства векторного произведения:

1. [а b] = - [ b а ] 2. [а + b, d ] = [а d] + [ b d]

3. [а, b]= [а,b]= [а b] 4. [а b]=0  a и b коллинеарны

Пример. Найти площадь треугольника, заданного тремя вершинами с координатами: A(-1,0,2), B(1,-2,5), C(3,0,-4).

Решение. Пусть вектор а расположен между вершинами А и В, а вектор b – между вершинами А и С. Тогда координаты образующих векторов:

ВА = а = (2, -2, 3), СА = b = (4, 0, -6)

и по формулам (4), (5) находим

S_треуг = S_парал 0.5 =

Определение 2. Пусть a,b,с вектора в пространстве R³ с ортонормированным базисом е₁, е_2, е₃. Смешанным произведением трех векторов a, b, c называется число, равное векторному произведению [ a b ], умноженному скалярно на вектор с.

Смешанное произведение обозначается символом ([а x b],c) (6)

Комментарии к определению.

1. Определение смешанного произведения связано с определенным порядком перемножаемых векторов: a- первый, b- второй, с- третий.

2. Базис фигурирует в определении в связи с тем, что формула (6) содержит векторное произведение [а x b], которое, как известно, зависит от того, каков базис пространства. Таким образом, для вычисления смешанного произведения, кроме самих векторов a,b,с надо знать ориентацию базиса.

3. При вычислении смешанного произведения удобно пользоваться следующей формулой: если векторы a, b, c заданы своими координатами, то их

смешанное произведение вычисляется по формуле

a₁ a₂ a₃

abc = b₁ b₂ b₃ (7)

c₁ c₂ c₃

Смешанное произведение (число) аbc по абсолютной величине равно объему параллепипеда, построенного на векторах a, b, c. Знак плюс соответствует случаю, когда тройки a, b, c и е₁, е_2, е₃ имеют одинаковую ориентацию, а знак минус – в противном случае.

Равенство аbc = 0 является необходимом и достаточном условием, что все три вектора лежат в одной плоскости (в таком случае вектора называют компланарными).