§ 3.5 Линейная оболочка

Определение 1. Линейной оболочкой заданной конечной совокупности элементов векторного пространства ⁿ над полем К называется множество всех линейных комбинаций этих элементов с коэффициентами из поля К. При этом сама совокупность называется порождающей системой данной линейной оболочки, а сама линейная оболочка обозначается символом .

Линейные оболочки обладают следующими свойствами:

. Линейная оболочка элементов векторного пространства ⁿ является подпространством М векторного пространства ⁿ.

Данный результат следует из определения линейной оболочки: сумма двух векторов из линейной оболочки будет принадлежать линейной оболочки (одна из линейных комбинаций), произведение вектора из линейной оболочки также будет принадлежать линейной оболочки.

. Линейная оболочка может совпадать со всем пространством Rⁿ (если образующая система является базисом в пространстве Rⁿ )

. Линейная оболочка является наименьшим подпространством, содержащим элементы . Все остальные подпространства могут только содержать вектора порождающей системы или их возможные комбинации.

. Если какой-нибудь элемент из порождающей системы элементов есть линейная комбинация остальных элементов этой системы, то его можно удалить из порождающей системы, не изменив при этом линейной оболочки.

. Если координатная матрица системы образующих имеет ранг р, где , то любая линейно независимая система , является базисом линейной оболочки , а сама линейная оболочка будет подпространством размерности р, .

Примеры.

1. Если a, b, с – геометрические векторы, лежащие на одной прямой. В этом случае линейная оболочка L(а,b,c)= L(a).Здесь линейная оболочка является одномерным пространством, которое состоит из всех вектор, лежащих на прямой, причем вектор а –является базисом.

2. Пусть a, b, с – геометрические векторы, причем a, b не коллинеарны, с = а + b. В этом случае линейная оболочка L(а,b,c)= L(a,b).Здесь линейная оболочка является двумерным пространством, состоящем из всех векторов, компланарных с векторами a и b. Вектора а,b составляют базис в L(a,b). Любой вектор из L представляется в виде линейной комбинации векторов а и b.

Вообще, в конечномерном пространстве R всякое подпространство L

является линейной оболочкой некоторой системы векторов.

Рассмотри следующую задачу. В евклидовом пространстве Eⁿ задана линейная оболочка , где k  n. Требуется:

1)Найти размерность и базис линейной оболочки ; 2)Выделить в линейной оболочке ортогональный базис и

достроить его до ортонормированного базиса евклидова

пространства Eⁿ.

Если схема решения первой задачи нам знакома, то решение второй задачи строится на следующем теоретическом результате.

Теорема (Грама – Шмидта)

Пусть - система линейно независимых векторов в евклидовом пространстве, где k  n, являющихся образующей системой линейной оболочки . Система векторов , описываемая формулами

, , , . . .

где коэффициенты , ,

образует ортогональный базис линейной оболочки .

Доказательство. Для доказательства теоремы достаточно доказать следующее утверждение: вектор ортогонален вектору .

Действительно, умножая скалярно вектор на вектор , получим

==0

Следствие. Результат теоремы дает алгоритм последовательной ортогонализации системы линейно независимых элементов ( так называемый метод Грама - Шмидта).

Пример

1. В евклидовом пространстве E⁴ линейная оболочка задана образующей системой векторов 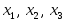с координатами

.

Требуется:

а) найти размерность и базис линейной оболочки

б) указать в линейной оболочке ортонормированный базис

и достроить его до ортонормированного базиса евклидова

пространства E⁴.

Решение. Рассмотрим координатную матрицу . Так как

,

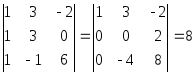то , элементы линейно независимы в E⁴ и образуют базис данной линейной оболочки, являющейся подпространством в E⁴.

Для построения ортонормированного базиса в E⁴ применим метод ортогонализации Грама-Шмидта. Получим

, , .

Записывая векторы столбцами их координат, последовательно найдем

.

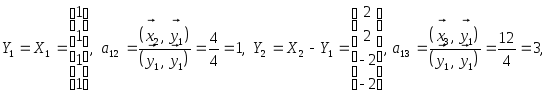
Легко проверить, что полученные элементы попарно ортогональны. Найдем ортогональный им вектор .

Пусть , то неизвестные координаты вектора Y₄ найдутся из условий

,,.

Так как 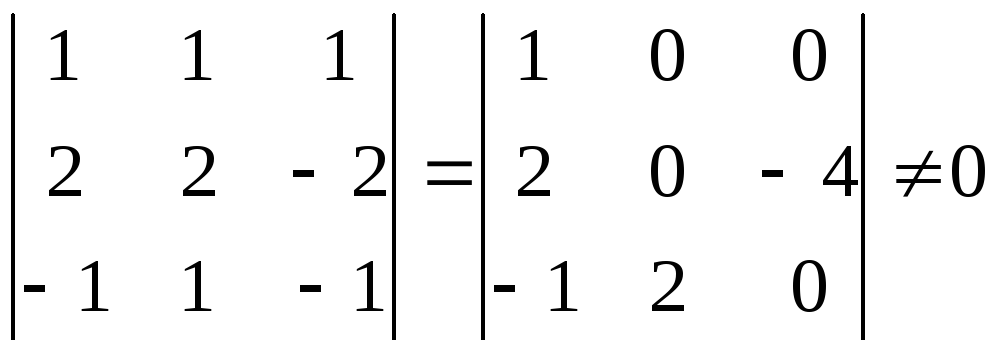, в последней системе неизвестные можно взять в качестве базисных неизвестных.

Если для свободной (небазисной) неизвестной , то .

Нормировав найденные векторы , построим ортонормированный базис в E⁴:

.

Задача решена.

В завершении параграфа введем важное определение.

Пусть - - базис в Eⁿ и векторы представлены в этом базисе своими разложениями

.

Тогда скалярное произведение этих векторов имеет вид или в матричной форме , где - столбцы координат векторов в базисе а симметричная матрица составлена из скалярных произведений базисных векторов:

.

В общем случае в качестве элементов матрицы А рассматривают скалярные произведения произвольной системы векторов а₁, а₂,…, а_n

Определение 3. Определитель матрицы А скалярных произведений заданной системы векторов называют определителем Грама.

Теорема Произвольная система векторов, заданных в ортонормированном базисе, будет линейно независимой, если ее определитель Грама отличен от нуля.