Глава 3. Векторное пространство

§ 3.1 Основные определения

При введении понятия линейного пространства (см. глава 1) абстрагируются не только от конкретной природы изучаемых объектов, но и от конкретного вида правил образования суммы элементов и произведения элемента на число (примеры с матрицами). Важно лишь, чтобы эти правила удовлетворяли восьми аксиомам, входящим в определение линейного пространства.

Определение 1. Упорядоченная совокупность n чисел а₁, а₂, …,а_n называется n-мерным вектором и обозначается а =(а₁, а₂, …,а_n ), где числа а₁, а₂, …,а_n называют координатами вектора, а число n - размерностью вектора.

Определение 2. Множество наборов из n чисел (векторов ) называется n-мерным векторным (или координатным) пространством над полем К, если выполнены следующие требования:

А) Имеется правило, по которому любым двум элементам и множества ставится в соответствие третий элемент этого множества, называемый суммой элементов и и обозначаемый символом .

В) Имеется правило , по которому любому элементу множества и любому числу из числового поля К (для нас вещественного) ставится в соответствие элемент из этого множества, называемый произведением элемента на число и обозначаемый символом или .

С) Указанные два правила удовлетворяют следующим восьми аксиомам.

Аксиомы операции сложения элементов:

(коммутативность суммы элементов).

(ассоциативность суммы).

Существует элемент такой, что

существует элемент такой, что .

Аксиомы операции умножения на число:

(особая роль числового множителя 1).

и

(ассоциативность относительно чисел).

Аксиомы, связывающие операции сложения и умножения на число:

и

(дистрибутивность относительно суммы числовых множителей).

и

(дистрибутивность относительно суммы элементов).

Определение 3. Два n-мерных вектора считаются равными, если их одноименные координаты (с одинаковыми номерами) равны.

Если все координаты равны нулю, то вектор называют нулевым.

Определение 4. Суммой 2-х векторов а=(а₁,а₂, …,а_n),b=(b₁,b₂, …,b_n) называется вектор с = а + b, каждая координата которого равна сумме одноименных координат слагаемых векторов с = а + b =(а₁ + b₁ , а₂ + b₂ ,…,а_n + b_n )

Определение 5. Разностью 2-х векторов а = (а₁, а₂, …,а_n ) и b = (b₁, b₂, …,b_n) называется вектор с = а - b , каждая координата которого равна разности одноименных координат слагаемых векторов с = а - b =(а₁ - b₁ , а₂ - b₂ ,…,а_n - b_n )

Определение 6. Произведением числа  на n-мерный вектор а =(а₁, а₂, …,а_n ) называется вектор а =(а₁, а₂, …,а_n )

Определение 7 Два вектора a и b называются коллинеарными, если существует число   0, такое что а = b

§ 3.2 Геометрическая интерпретация вектора

Если рассматривать координатную ось ОХ, на которой зафиксирована точка О (начало координат), выбрано положительное направление и введена метрика (единица длины), то выбранный между двумя точками прямой А и В отрезок будет обладать определенным размером – (длиной), обозначаемой . Если одну из точек прямой А принять за начало, а другую В за конец, то отрезок будет иметь направление.

Определение 1. Отрезок, имеющий определенную длину и определенное направление называют направленным отрезком и обозначают .

Длина направленного отрезка обозначается .

Если рассматривать совокупность двух взаимно перпендикулярных координатных осей, имеющих общее начало (декартова система координат, задающая пространство размерности 2 или плоскость R²), то каждые две точки А и В такой плоскости можно соединить направленным отрезком.

Y

У₂ В

У₁ А

0 А₁ В₁ X

х₁ х₂

Основание А₁ и В₁ перпендикуляров АА₁ и ВВ₁ , опущенные на ось Ох, называют проекциями точек А и В на ось Ох. Если точки А и В лежат на оси, то проекции отрезка совпадают с самим отрезком. Аналогично рассматривают проекции на ось Оу. Направленный отрезок, соединяющий проекции точек А и В на осях обозначают Пр_ОХили Пр_ОY. Иногда Пр_ОХили Пр_ОY называют геометрической проекцией отрезка .

Определение 2. Арифметической проекцией отрезка называют положительное число, равное длине отрезка Пр_ОХ, если отрезок и ось Ох одинаково направлены и отрицательное число Пр_ОХ,если отрезок и ось Ох противоположно направлены.

Отметим некоторые свойства проекций направленного отрезка.

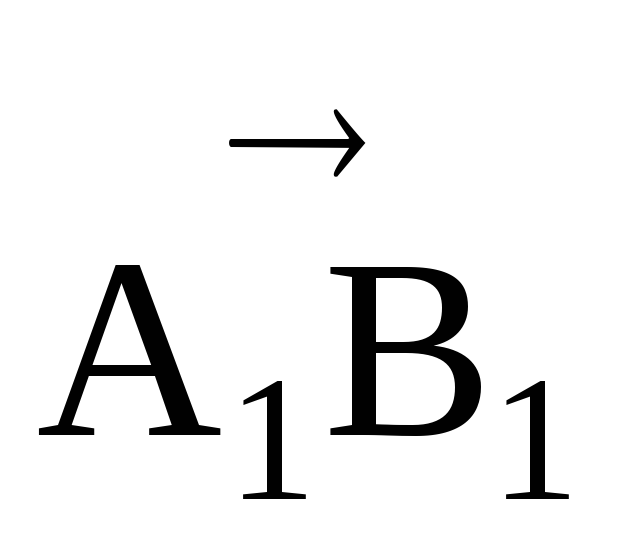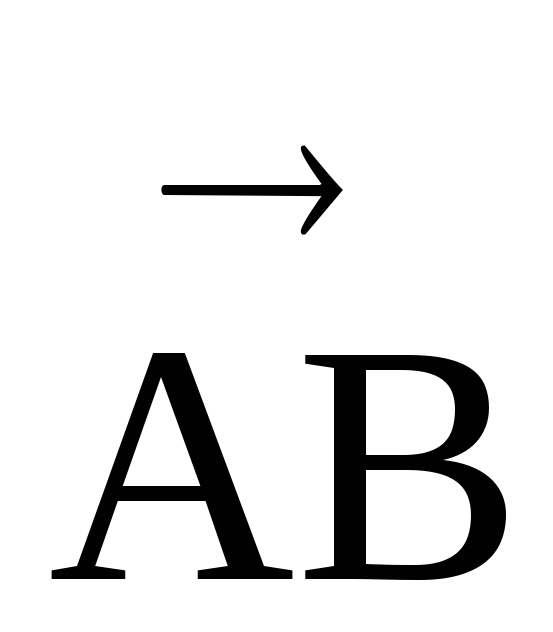
1. Проекция отрезка на ось ОХ равна произведению длины данного отрезка на косинус угла  между отрезком и данной осью: Пр_ОХ=  cos.

2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось

С введением проекций длина направленного отрезка может быть определена по теореме Пифагора:

 = .

Если рассматривать совокупность трех взаимно перпендикулярных координатных осей, имеющих общее начало (декартова система координат, задающая пространство размерности 3 или R³), то каждые две точки А и В такого пространства также соединяется направленным отрезком.

Y

У₂ В

У₁ А

0 x₁ x₂ X

z₁

z₂

Z

Распространив введенное понятие проекции на все три оси, можно получить формулу длины направленного отрезка АВ :

 =

Если длина отрезка в данном пространстве определяется по представленным формулам, то говорят, что в таком пространстве введена Евклидова мера.

Определение 3. Два направленных отрезка коллинеарны, если они лежат на одной прямой или на параллельных прямых (сравните с определение п.3.1 для векторов).

Определение 4. Два направленных отрезка будут равны, если они коллинеарны, одинаково направлены и имеют одинаковые длины.

Другое определение: направленные отрезки равны, если их геометрические и арифметические проекции совпадают.

Определение 5. Совокупность равных по длине и одинаково направленных отрезков называют вектором.

Данное определение вектора удобно применять к векторам, расположенным в координатных пространствах размерности 2 и 3. Кроме того, определение позволяет рассматривать вектор, как объект, инвариантный (т.е. сохраняющий свои свойства) относительного расположения в любой области данного пространства. В силу этого, рассматривают не начало и конец вектора , а только его конечную точку, считая, что начало вектора перемещено в начало координатной системы, т.е. в точку с нулевыми координатами. В этом случае, вектор обозначают а или . В дальнейшем тексте используются оба обозначения.

Рассмотрим линейные операции над геометрическими векторами.

1. Сумма двух векторов строится либо по правилу треугольника, либо по правилу параллелограмма, т.е.

а

b то a b или а

a + b b

2. Под разностью векторов a и b понимают вектор с = a – b такой, что b + c = a.

3. Произведением вектора а на число  называют вектор  а, который имеет длину а, коллинеарен вектору а, имеет направление вектора а, если >0 и противоположное направление, если <0.

Определение 6. Вектора единичной длины, расположенные на осях декартовой системы с началом в центре координат, называют ортами.

Если рассматривается пространство размерности 2, то орты, расположенные на осях Ох и Оу обозначают, соответственно, i и j, а в пространстве размерности 3 – орты, расположенные на осях Ох, Оy и Oz обозначают - i, j и k.

Z

k i Х

j

Y