3.3. Энергия электрического поля.

Объемная плотность энергии

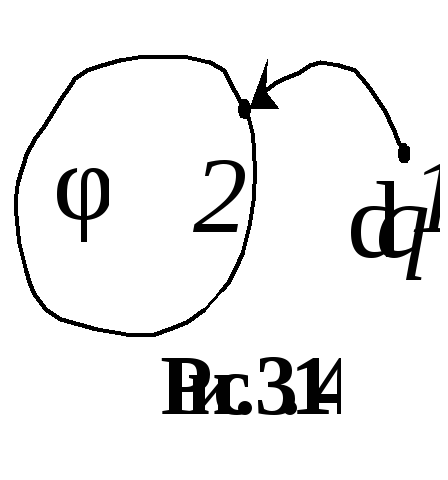
Рассмотрим процесс зарядки уединенного проводника. Чтобы его заряд достиг величины Q, будем сообщать проводнику заряд порциями dq, перенося их из бесконечно удаленной точки 1 на поверхность проводника в точку 2 (рис. 3.14). Для передачи проводнику новой порции заряда внешние силы должны совершить работу против сил электрического поля : . Поскольку проводник уединенный (точка 1 бесконечно далека от проводника), то . Потенциал точки 2 равен потенциалу проводника . Поэтому . Если проводнику передан заряд q, то его потенциал . Полная работа внешних сил по зарядке проводника до значения заряда Q будет равна

.

Согласно закону сохранения энергии, работа внешних сил по зарядке проводника увеличивает энергию создаваемого электростатического поля, т.е. проводник запасает определенную энергию:

. (3.13)

Рассмотрим процесс зарядки конденсатора от источника ЭДС. Источник в процессе зарядки переносит заряды с одной пластины на другую, причем сторонние силы источника совершают работу по увеличению энергии конденсатора:

,

где Q – заряд конденсатора после зарядки. Тогда энергия электрического поля, созданного конденсатором, определится как

. (3.14)

Выражение (3.14) позволяет записать величину энергии электростатического поля двумя способами:

и .

Сопоставление двух соотношений позволяет задать вопрос: что является носителем электрической энергии? Заряды (первая формула) или поле (вторая формула)? Оба записанных равенства прекрасно согласуются с результатами экспериментов, т.е. расчет энергии поля можно одинаково правильно вести по обеим формулам. Однако такое наблюдается только в электростатике, т.е. когда осуществляется расчет энергии поля неподвижных зарядов. При рассмотрении теории электромагнитного поля в дальнейшем (гл. 8) мы увидим, что электрическое поле может создаваться не только неподвижными зарядами. Электростатическое поле – это частный случай электромагнитного поля, существующего в пространстве в виде электромагнитной волны. Его энергия распределена в пространстве с определенной плотностью. Введем понятие объемной плотности энергии поля следующим образом.

Преобразуем последнее равенство (3.14) для случая плоского конденсатора, воспользовавшись связью разности потенциалов и напряженности однородного поля:

,

где – объем конденсатора, т.е. объем части пространства, в котором создано электрическое поле.

Объемной плотностью энергии поля называется отношение энергии поля, заключенного в малом объеме пространства к этому объему:

. (3.15)

Следовательно, энергию однородного электрического поля можно рассчитать так: .

Сделанный вывод можно распространить на случай неоднородного поля таким образом:

, (3.16)

где – такой элементарный объем пространства, в пределах которого поле можно считать однородным.

Для примера рассчитаем энергию электрического поля, созданного уединенным металлическим шаром радиусом R, заряженным зарядом Q, и находящимся в среде с относительной диэлектрической проницаемостью . Повторив рассуждения примера из п.2.5, получим модуль напряженности поля в виде функции :

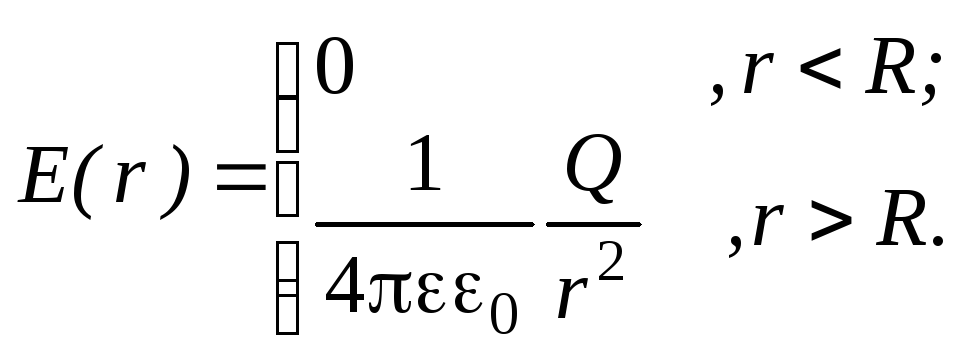
Тогда выражение для объемной плотности энергии поля примет вид:

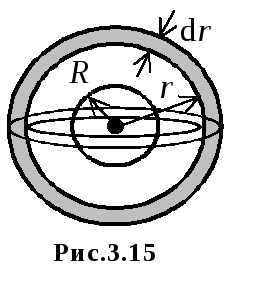
Поскольку напряженность поля зависит только от радиальной координаты, то она будет практически постоянна в пределах тонкого сферического слоя с внутренним радиусом r и толщиной (рис. 3.15). Объем этого слоя . Тогда энергия поля определится так:

.

Аналогичный результат мы бы получили, если бы вычисляли энергию заряженного шара по формуле (3.13), воспользовавшись (3.6):

.

Однако следует помнить, что такой способ неприменим, если необходимо найти энергию электрического поля, заключенную не во всем объеме поля, а лишь в его части. Также метод расчета по формуле (3.13) нельзя использовать при определении энергии поля системы, для которой неприменимо понятие “емкость”.