
Физика 3 семестр / новая папка / Помощь к экзамену / Темы / 15.Циркуляция вектора магнитной индукции
.doc5.2. Поток магнитной индукции. Теорема о циркуляции
магнитной индукции
Назовем элементарным потоком индукции магнитного поля (магнитным потоком) через малый участок поверхности S величину
![]() ,
(5.18)
,
(5.18)
где
![]() –
вектор площади элемента поверхности,
–
вектор площади элемента поверхности,
![]() – вектор единичной нормали к поверхности
в месте расположения элемента
– вектор единичной нормали к поверхности
в месте расположения элемента
![]() (рис.5.10).
Справедливы соотношения:
(рис.5.10).
Справедливы соотношения:
![]() ;
;
![]() .
Малый элемент поверхности
.
Малый элемент поверхности
![]() выбирается таких размеров, чтобы его
можно было считать плоским, а магнитное
поле в его пределах можно было считать
однородным. Магнитный поток через всю
поверхность S
находится как алгебраическая сумма
потоков сквозь все малые участки этой
поверхности:
выбирается таких размеров, чтобы его
можно было считать плоским, а магнитное
поле в его пределах можно было считать
однородным. Магнитный поток через всю
поверхность S
находится как алгебраическая сумма
потоков сквозь все малые участки этой
поверхности:
![]() .
(5.19)
.
(5.19)

![]() в одну и ту же сторону по отношению к
поверхности S.
Например, в случае замкнутой поверхности
S
в дальнейшем будем считать векторы
в одну и ту же сторону по отношению к
поверхности S.
Например, в случае замкнутой поверхности
S
в дальнейшем будем считать векторы
![]() внешними нормалями,
т.е. направленными из
области, ограниченной этой поверхностью.
По своему физическому смыслу магнитный
поток аналогичен потоку вектора
напряженности электрического поля:
магнитный поток через
поверхность пропорционален числу линий
магнитной индукции, пересекающих эту
поверхность.
внешними нормалями,
т.е. направленными из
области, ограниченной этой поверхностью.
По своему физическому смыслу магнитный
поток аналогичен потоку вектора
напряженности электрического поля:
магнитный поток через
поверхность пропорционален числу линий
магнитной индукции, пересекающих эту
поверхность.
Единица измерения магнитного потока в СИ называется вебер (обозначение Вб в честь немецкого физика В.Э. Вебера, предложившего вместе с К.Ф. Гауссом систему единиц для электрических величин): 1 вебер – это поток однородного магнитного поля с индукцией 1 тесла через поверхность площадью 1 м2, расположенную перпендикулярно линиям магнитной индукции; 1Вб = = 1 Тл1 м2.
Поскольку линии магнитной индукции всегда замкнуты сами на себя, то при вычислении магнитного потока через любую замкнутую поверхность необходимо учитывать, что число линий индукции, пересекающих поверхность в одну сторону (“входящих в нее”), всегда равно числу линий индукции, пересекающих поверхность в другую сторону (“выходящих в нее”). Поэтому суммарный магнитный поток через любую замкнутую поверхность всегда равен нулю:
![]() .
(5.20)
.
(5.20)
Соотношение (5.20) выражает теорему Остроградского–Гаусса для магнитного поля. Сравнение этой формулы с (1.26) показывает, что в природе нет магнитных зарядов, т.е. источников магнитного поля, на которых начинались бы или заканчивались линии магнитной индукции. Опыты показали, что, разрезая постоянный магнит на части, нельзя разделить его полюсы, т.е. нельзя получить магнит либо с одним северным, либо с одним южным полюсом. Для сравнения вспомним, что, разрезав проводник, помещенный в электростатическое поле, в котором произошла электростатическая индукция (см. рис. 3.1), на две части, мы получим два разноименно заряженных тела. Следовательно, в отличие от электрических зарядов, магнитных зарядов действительно не существует.
Магнитный
поток через поверхность, ограниченную
замкнутым контуром, называют
потокосцеплением
![]() этого контура. Например, потокосцепление
рамки или катушки, состоящей из N
витков, магнитные потоки через которые
одинаковы и равны
этого контура. Например, потокосцепление
рамки или катушки, состоящей из N
витков, магнитные потоки через которые
одинаковы и равны
![]() ,
будет выражаться как
,
будет выражаться как
![]() .
.
Вспомним, что для электростатического поля было получено условие его потенциальности (1.11). Рассчитаем циркуляцию индукции магнитного поля вдоль произвольного контура.

![]() .
Направление
.
Направление
![]() при выбранном направлении тока в
проводнике указано на рис. 5.11 в соответствии
с правилом буравчика. Выберем нарисованную
окружность радиуса r
в качестве произвольного контура для
расчета циркуляции магнитной индукции,
причем направление обхода контура
согласуем с направлением линии магнитной
индукции по правилу правого винта. Тогда
элемент окружности – вектор
при выбранном направлении тока в
проводнике указано на рис. 5.11 в соответствии
с правилом буравчика. Выберем нарисованную
окружность радиуса r
в качестве произвольного контура для
расчета циркуляции магнитной индукции,
причем направление обхода контура
согласуем с направлением линии магнитной
индукции по правилу правого винта. Тогда
элемент окружности – вектор
![]() –
совпадает в каждой точке по направлению
с вектором
–
совпадает в каждой точке по направлению
с вектором
![]() .
Тогда
.
Тогда
![]() ,
,
где
![]() –
угол, под которым элемент
–
угол, под которым элемент
![]() виден из центра окружности. Циркуляция
виден из центра окружности. Циркуляция
![]() по всему замкнутому контуру будет
определяться так:
по всему замкнутому контуру будет
определяться так:
![]() .
(5.21)
.
(5.21)
Таким образом, в отличие от циркуляции напряженности электростатического поля, циркуляция магнитной индукции по замкнутому контуру не равна нулю, следовательно, магнитное поле не является потенциальным.
Если в качестве замкнутого контура интегрирования выбрана не окружность, совпадающая с линией магнитной индукции, а произвольная кривая (рис. 5.12), то
![]() .
.
Таким образом, все равно циркуляция магнитной индукции по произвольному замкнутому контуру отлична от нуля:
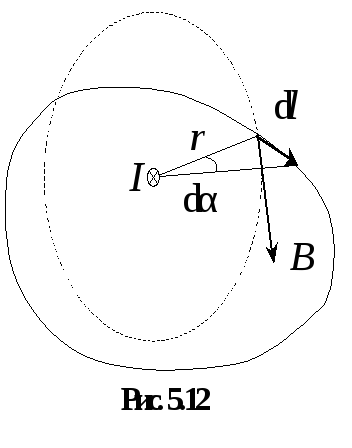
![]() .
.
Отметим, что в случаях,
изображенных на рис.5.11 и 5.12, контуры
интегрирования “охватывали” проводник
с током, т.е. проводник с током пересекал
поверхность, ограниченную контуром L.
Такой проводник (или ток) называют
проводником (током), сцепленным
с контуром. Рассмотрим, чему будет
равна циркуляция магнитной индукции
по произвольному замкнутому контуру,
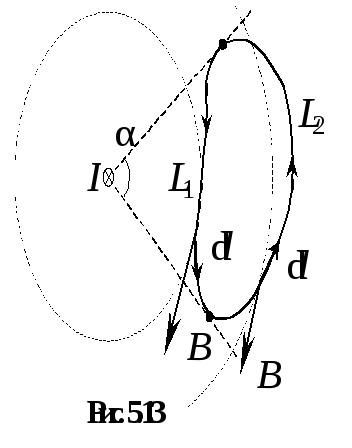
не охватывающему ток. В этом случае
(рис.5.13) весь контур L
разбивается на две части
![]() и
и
![]() .На
части контура
.На
части контура
![]() угол между векторами
угол между векторами
![]() и
и
![]() острый (
острый (![]() ),
а на части контура
),
а на части контура
![]() угол между векторами
угол между векторами
![]() и
и
![]() тупой (
тупой (![]() ).
Тогда
).
Тогда
![]() .
(5.22)
.
(5.22)
Итак, если ток не сцеплен с контуром интегрирования, то циркуляция магнитной индукции по такому контуру равна нулю.
Если магнитное поле создается системой токов, то применим принцип суперпозиции магнитных полей. Однако необходимо учитывать согласование направления обхода контура интегрирования и направления токов. В примере, изображенном на рис. 5.14, мы получим
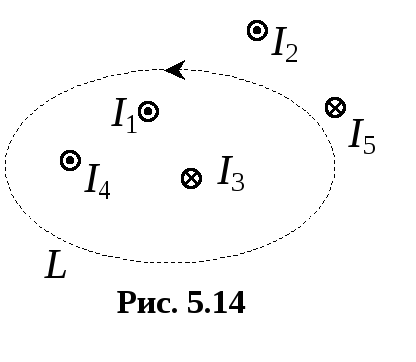
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() –
магнитная индукция поля, созданного
проводником с током силой
–
магнитная индукция поля, созданного
проводником с током силой
![]() .
Тогда
.
Тогда
![]() .
(5.23)
.
(5.23)
Объединяя все выводы (5.21)–(5.23) в один, можно сформулировать общее правило: циркуляция вектора магнитной индукции по произвольному замкнутому контуру прямо пропорциональна алгебраической сумме токов, сцепленных с этим контуром, причем направление обхода контура и направление тока связаны правилом буравчика. Этот вывод называется теоремой о циркуляции магнитной индукции:
.
![]() (5.24)
(5.24)
Еще раз подчеркнем, что, поскольку циркуляция магнитной индукции по произвольному замкнутому контуру в общем случае отлична от нуля, то магнитное поле не является потенциальным. Оно относится к вихревым физическим полям. Вихревой характер поля означает, что его линии индукции замкнуты сами на себя, а неподвижные “магнитные заряды”, создающие такое поле, в природе отсутствуют.
Очень
часто теорему о циркуляции магнитной
индукции называют законом
полного тока,
поскольку в правой части выражения
(5.24) записана алгебраическая сумма токов
(полный ток), сцепленных с контуром L.
Рассмотрим применение закона полного
тока для определения магнитной индукции
различных полей. Оно особенно удобно
для расчета магнитных полей симметричных
систем токов. В этом случае можно так
выбрать контур интегрирования, что
циркуляция магнитной индукции поля
вдоль него легко выражается через
искомое значение модуля вектора
![]() .
Решение задачи о нахождении индукции
поля в какой-либо точке пространства
должно осуществляться следующим образом:
.
Решение задачи о нахождении индукции
поля в какой-либо точке пространства
должно осуществляться следующим образом:
1.
Исходя из симметрии распределения
заданной системы токов в пространстве
необходимо построить линии магнитной
индукции поля, т.е. определить направление
вектора
![]() в любой точке пространства.
в любой точке пространства.
2. Выбрать “удобный” замкнутый контур интегрирования, отвеча-ющий следующим требованиям:
а) он должен проходить через исследуемую точку;
б) длина контура должна быть известна;
в) модуль индукции поля должен быть постоянен в точках всего контура или хотя бы его части;
г)
угол между
![]() и касательной к контуру должен быть
известен в любой точке контура (это
обеспечивается выполнением п. 1).
и касательной к контуру должен быть
известен в любой точке контура (это
обеспечивается выполнением п. 1).
3. Определить циркуляцию магнитной индукции по выбранному замкнутому контуру. Если выполнено условие п.2в, то
![]() ,
,
где
![]() –
постоянный модуль магнитной индукции
во всех точках части контура
–
постоянный модуль магнитной индукции
во всех точках части контура
![]() .
.
4. Определить алгебраическую сумму токов, сцепленных с контуром L.
5. Применить теорему, т.е. приравнять результаты, полученные в пп.3 и 4 с учетом коэффициента пропорциональности.
 Пример.
Определим магнитную индукцию поля
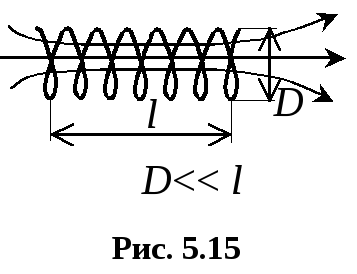
бесконечно длинного
соленоида. Таким термином
называется катушка, образованная
одинаковыми плотно прилегающими друг
к другу витками (рис.5.15), причем длина
катушки существенно больше ее диаметра.
В этом случае суперпозиция полей каждого
витка (см. рис. 5.8) приводит к образованию
внутри соленоида однородного магнитного
поля, кривизной линий индукции которого
вблизи центра соленоида можно пренебречь.
Линии магнитной индукции такого поля
параллельны друг другу, а модуль индукции
одинаков во всех точках вблизи центра
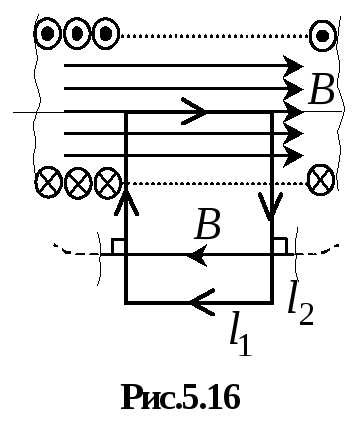
соленоида. Выберем контур интегрирования
L
в виде прямоугольника, направление
обхода которого указано на рис. 5.16.
Короткая сторона контура параллельна
оси системы, длина ее равна
Пример.
Определим магнитную индукцию поля
бесконечно длинного
соленоида. Таким термином
называется катушка, образованная
одинаковыми плотно прилегающими друг
к другу витками (рис.5.15), причем длина
катушки существенно больше ее диаметра.
В этом случае суперпозиция полей каждого
витка (см. рис. 5.8) приводит к образованию
внутри соленоида однородного магнитного
поля, кривизной линий индукции которого
вблизи центра соленоида можно пренебречь.
Линии магнитной индукции такого поля
параллельны друг другу, а модуль индукции
одинаков во всех точках вблизи центра
соленоида. Выберем контур интегрирования
L
в виде прямоугольника, направление
обхода которого указано на рис. 5.16.
Короткая сторона контура параллельна
оси системы, длина ее равна
![]() .
Длинная сторона контура имеет длину
.
Длинная сторона контура имеет длину
![]() .
Поскольку соленоид бесконечно длинный,
линии магнитной индукции вне соленоида,
замыкаясь сами на себя, остаются
параллельными его оси, а поэтому
циркуляция
.
Поскольку соленоид бесконечно длинный,
линии магнитной индукции вне соленоида,
замыкаясь сами на себя, остаются
параллельными его оси, а поэтому
циркуляция
![]() вдоль боковых сторон контура L
равна нулю:
вдоль боковых сторон контура L
равна нулю:
![]() .
.
Если
![]() ,
то модуль магнитной индукции в точках
дальней от соленоида стороны контура
стремится к нулю, поэтому
,
то модуль магнитной индукции в точках
дальней от соленоида стороны контура
стремится к нулю, поэтому
![]() .
(5.25)
.
(5.25)
Алгебраическая
сумма токов, сцепленных с контуром L,
определится числом витков соленоида,
расположенных на длине отрезка
![]() :
:
![]() .
(5.26)
.
(5.26)
Применим закон полного тока, приравняв выражения (5.25) и (5.26) с учетом коэффициента:
![]() .
.
Тогда модуль магнитной индукции в центре бесконечно длинного соленоида (на его оси) выражается так:
![]() .
(5.27)
.
(5.27)
Модуль
![]() на краю бесконечно длинного соленоида
(на его оси) можно
найти следующим образом. Поскольку
любой бесконечно длинный соленоид можно
представить в виде последовательно
соединенных двух бесконечно длинных
соленоидов (рис. 5.17), то
на краю бесконечно длинного соленоида
(на его оси) можно
найти следующим образом. Поскольку
любой бесконечно длинный соленоид можно
представить в виде последовательно
соединенных двух бесконечно длинных
соленоидов (рис. 5.17), то
![]() ,
где
,
где
![]() .
Тогда
.
Тогда
![]() .
(5.28)
.
(5.28)
