1.2. Расчет магнитной цепи постоянного магнита

Постоянные магниты широко применяются в измерительных приборах, реле, генераторах и т. д.

Н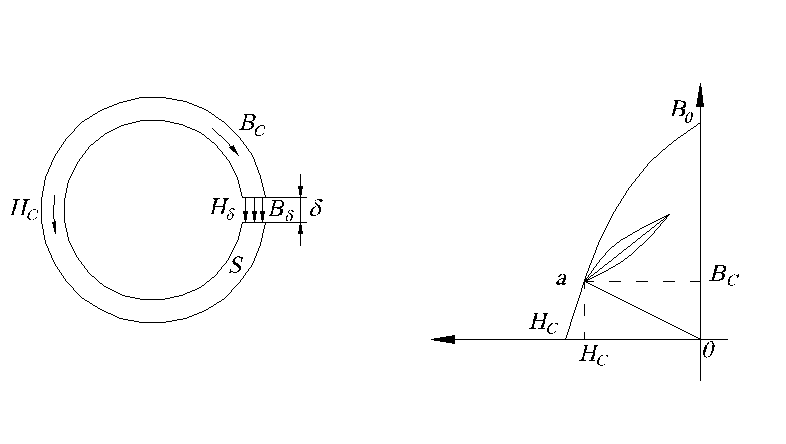а рис.1.4 изображено тороидальное кольцо с воздушным зазором.

а) б)

Рис.1.4. Тороидальный магнитопровод с воздушным зазором (а) и его кривая размагничивания (б).

Если бы не было воздушного зазора, то, как видно из кривой размагничивания (рис.1.4б), напряженность в сердечнике равнялась бы нулю H_c=0, а индукция B_c в сердечнике равнялась бы остаточной индукции B₀.

Из закона полного тока имеем: .

Здесь

– магнитное напряжение воздушного зазора;

l_c – длина средней линии тороида.

Напряженность магнитного поля в воздушном зазоре: .

Если зазор достаточно мал, то можно пренебречь потоком рассеяния и считать, что поток в магните равен потоку в зазоре: ,

отсюда

; .

Воспользовавшись выражением можно написать:

;

; (1.9)

коэффициент носит название размагничивающего фактора.

Проведем прямую H_c= -NB_c из точки 0 до пересечения с кривой размагничивания (рис.1.4б). Координаты точки пересечения определяют напряженность магнитного поля H_c и индукцию B_c. Если теперь уменьшить величину зазора, то магнитная индукция и напряженность будут определяться не кривой размагничивания, а, в силу наличия гистерезиса, частной петлей гистерезиса. Эту петлю называют линией возврата.

1.3. Механические усилия в магнитном поле

На проводник с током I, помещенный в магнитное поле индукции B, воздействует сила, направление которой определяется правилом левой руки (если вектор направлен в сторону ладони, а четыре пальца - вдоль тока в проводнике, то большой палец укажет направление силы).

(1.10)

где

-длина проводника с током.

а)

б)

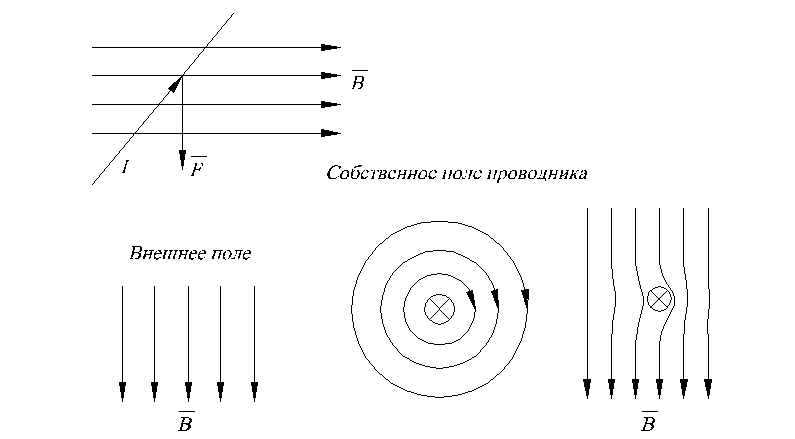
Рис.1.5. К определению направления действия механической силы в магнитном поле (а) и картины распределения магнитных силовых линий в поле проводника с током(б).

Механическое усилие, действующее на проводник с током в магнитном поле, объясняется стремлением силовых линий, искаженных действием тока, выпрямиться (рис. 1.5б).

Рис.1.6. К определению силы тяги электромагнита.

Сила тяги электромагнита (рис.1.6) определяется выражением

F=. (1.11)

1.4. Магнитная цепь с переменной магнитодвижущей силой (мдс)

На рис. 1.7а показана схема подключения катушки с ферромагнитным сердечником к источнику синусоидального напряжения.

Из закона Ома для магнитной цепи (1.7) () видно, что зависимость Ф=f(I) для катушки с ферромагнитным сердечником является нелинейной и ee характер определяется зависимостью B=f(H) (рис.1.7б). Так как L=w, то характер зависимости L=f(I) можно получить, построив зависимость (рис.1.7б).

а)

б)

Рис.1.7. Катушка с ферромагнитным сердечником, схема замещения ее магнитной цепи (а), зависимость магнитного потока и индуктивности катушки от тока (б).

Рассмотрим электромагнитные процессы в цепи катушки с ферромагнитным сердечником при подключении ее к синусоидальному напряжению (рис.1.8).

Рис.1.8. Схема замещения электрической цепи катушки с ферромагнитным сердечником.

На основании второго закона Кирхгофа имеем:

Активное падение напряжения ir относительно мало и для анализа общего характера процесса им можно пренебречь:

,

отсюда

Ф= -

Здесь A – постоянная величина магнитного потока, которая при питании синусоидальным напряжением (в установившемся режиме) равна нулю. Поэтому

, (1.12)

где

.

Будем считать, что начальная фаза потока равна 0, т.е.. Тогда , т.е. ЭДС отстает от индуцирующего ее потока на .

, где ;

;

. (1.13)

- уравнение трансформаторной ЭДС.

Связь между магнитным потоком и возбуждающим его током отображается петлей гистерезиса.

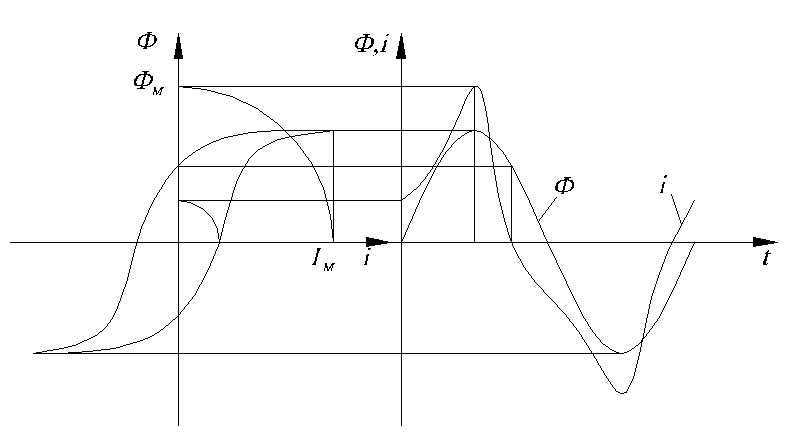
Рис.1.9. Построение кривой тока катушки с ферромагнитным сердечником.

Используя синусоидальную кривую потока и частный цикл гистерезиса, построим зависимость i(t) (рис.1.9). Анализ этой кривой показывает, что гистерезисная петля приводит к появлению угла сдвига фаз между потоком и вызывающим его током. Насыщение сердечника приводит к появлению пика в кривой тока. Чем больше величина магнитной индукции в сердечнике, тем больше и острее этот пик, что говорит о несинусоидальности кривой тока.

Заменим несинусоидальный ток эквивалентным синусоидальным. Условием эквивалентности является равенство действующих значений этих токов и равенство потерь, которые они вызывают. Эта замена позволит использовать методы расчетов цепей синусоидального тока и построить векторную диаграмму для катушки с ферромагнитным сердечником. Так как между несинусоидальным током и потоком существует сдвиг фаз, то и эквивалентный синусоидальный ток опережает поток на угол , называемый углом магнитного запаздывания (рис.1.10).

Рис.1.10. Векторные диаграммы магнитного потока, ЭДС и тока катушки с ферромагнитным сердечником.

Величина угла определяется потерями в ферромагнитном проводнике от действия гистерезиса и вихревых токов.

Рассмотрим распределение магнитного потока в ферромагнитном сердечнике катушки (рис.1.11).

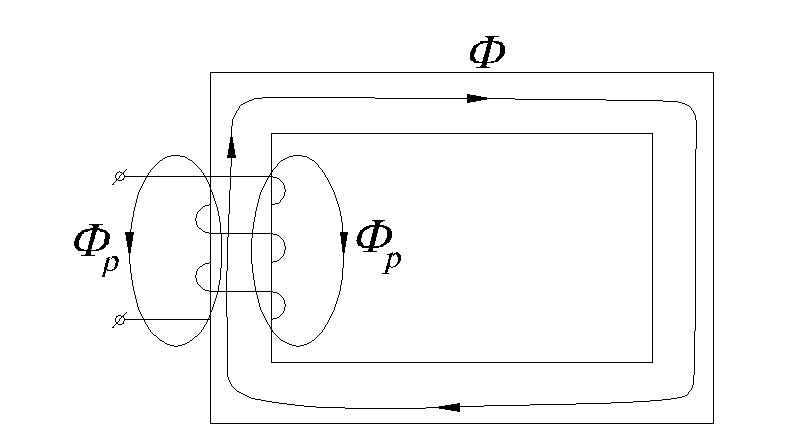
Рис.1.11. К определению магнитного потока рассеяния в катушке с ферромагнитным сердечником

Хотя магнитная проницаемость сердечника в несколько тысяч раз больше магнитной проницаемости воздуха, часть магнитного потока катушки замыкается не по сердечнику, а по воздуху. Эта часть потока носит название потока рассеивания Ф_р (рис. 1.11). Таким образом, полный поток, сцепленный с витками катушки равен

. (1.14)

На основании закона Ома для магнитной цепи (1.7) можно написать выражение для потока рассеяния:

. (1.15)

Так как , то .

То есть поток рассеяния , в отличие от потока в сердечнике, совпадает по фазе с током и связан с ним линейной зависимостью. Следовательно, на векторной диаграмме вектор потока будет совпадать с вектором тока (рис.1.12).

Рис.1.12. Векторная диаграмма магнитных потоков, ЭДС и токов катушки с ферромагнитным сердечником.

Будем считать, что все витки обмотки катушки с ферромагнитным сердечником сцеплены с Ф_р, тогда

;

L_р=;

;

;

; _m==;

;

Величина называется индуктивным сопротивлением рассеяния. В уравнении, составленном на основании 2-го закона Кирхгофа для электрической цепи катушки с ферромагнитным сердечником, к разности добавится :

U=-e+ri-e_р= -e+ri+L_р.

В комплексной форме

_р; (1.16)

, (1.17)

где

Z= r+jx_р; x_р=.

На рис.1.13 построена векторная диаграмма катушки с ферромагнитным сердечником.

Рис.1.13 Полная векторная диаграмма катушки с ферромагнитным сердечником.

Разложим вектор тока катушки на две составляющие:

; .

Используя векторную диаграмму, получим эквивалентную схему замещения катушки с ферромагнитным сердечником (рис.1.14).

Рис.1.14. Схема замещения катушки с ферромагнитным сердечником.

Из уравнения трансформаторной ЭДС (1.13) определяем число витков катушки:

w=; (выбирается в пределах .)

Ток намагничивания определяется по формуле:

I_ф=. (1.18)

Ток потерь в сердечнике:

I_n. (1.19)

Полный намагничивающий ток катушки:

I=. (1.20)

Приведем выражения, позволяющие рассчитать потери в сердечнике от гистерезиса и от вихревых токов. Потери в сердечнике от гистерезиса пропорциональны площади петли гистерезиса. Следует иметь ввиду, что ширина петли гистерезиса растет с увеличением частоты.

, (1.21)

где

- коэффициент потерь на гистерезис, зависящий от материала сердечника;

f – частота;

G – вес сердечника;

n=1,6 при B_m<1Тл и n=2 при B_m>1Тл.

Под действием переменного магнитного потока в сердечнике возникают вихревые токи (рис. 1.15).

Рис.1.15. К эффекту возникновения вихревых токов в ферромагнитном сердечнике.

Пусть вектор магнитного потока направлен, как показано на рис.1.15. Тогда в сердечнике, в плоскости перпендикулярной потоку возникнет ЭДС, под действием которой возникнут вихревые токи. Направление ЭДС таково, что создаваемый ими поток уменьшает вызвавший ЭДС поток . Для уменьшения потерь от вихревых токов сердечники (до частоты 20 кГц) собираются из листов ферромагнитного материала, изолированных друг от друга лаком. Другой способ уменьшения потерь от вихревых токов – увеличение сопротивления самого ферромагнитного материала за счет добавления нескольких процентов кремния, что оказывает незначительное влияние на его магнитные характеристики. При частотах до 50 МГц применяются сердечники из магнитодиэлектриков - прессмасс, состоящих из зерен ферромагнитного вещества, разделенных диэлектриком.

Потери на вихревые токи

; (1.22)

где

- коэффициент потерь от действия вихревых токов;

- коэффициент, учитывающий изоляцию листов.

1.5. Трансформаторы

Трансформатором называется статический электромагнитный аппарат, передающий энергию из одной цепи в другую посредством электромагнитной индукции. Он применяется для различных целей, но чаще всего служит для преобразования напряжения и тока.

Трансформаторы бывают: силовые, измерительные, специального назначения. Кроме того, трансформаторы различаются по числу фаз на однофазные и трехфазные; по способу охлаждения на сухие и жидкостные.

Условные обозначения трансформаторов (рис 1.16):

Рис.1.16. Условные обозначения трансформаторов: однофазного (а); трехфазного (б).