2.4.9. Электромеханическая постоянная времени исполнительных двигателей

Время разгона исполнительного двигателя определяется, главным образом, электромеханическими переходными процессами, т. к. из-за значительного активного сопротивления электромагнитные переходные процессы в них быстротечны. Электромеханическая постоянная времени примерно на порядок больше электромагнитной постоянной времени . Значение определяется из основного уравнения динамики для двигателя при условии разгона его ротора от неподвижного состояния до скорости холостого хода при статическом моменте на валу . При этих условиях основное уравнение динамики

принимает вид

, (2.105)

где

- момент инерции ротора.

Обычно электромеханическую постоянную времени определяют исходя из пускового момента . Для идеализированного двигателя при прямолинейной механической характеристике

, (2.106)

где

- скорость холостого хода.

Следовательно, можно записать

или

Решив это уравнение, получим

, (2.107)

где

- электромеханическая постоянная

времени:

(2.108)

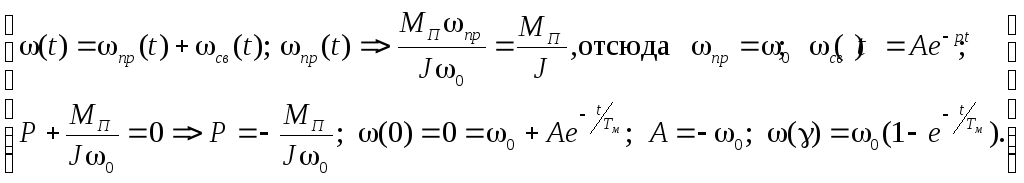
Физически электромеханическая постоянная времени представляет собой время, необходимое для разгона двигателя от неподвижного состояния до достижения скорости холостого хода при постоянном моменте на валу и . В действительности момент, действующий на вал ротора в процессе разгона уменьшается, вследствие чего время разгона до скорости оказывается большим .

В двигателе с амплитудным управлением

, (2.109)

где

- синхронная скорость, соответствующая круговому вращающемуся полю и пусковому моменту .

Поэтому

. (2.110)

Из этого выражения следует, что при амплитудном управлении постоянная времени растет с уменьшением эффективного коэффициента сигнала, т. к. уменьшается величина пускового момента. При фазовом управлении и . Поэтому

. (2.111)

Следовательно, при этом способе управления постоянная времени не зависит от коэффициента сигнала . Это объясняется тем, что при фазовом управлении механические характеристики параллельны – при уменьшении коэффициента сигнала пропорционально ему уменьшается момент при пуске и скорость холостого хода. В результате время разгона не изменяется. При амплитудном же управлении уменьшение сигнала приводит к такому же уменьшению момента, но скорость холостого хода уменьшается в меньшей степени. Так, например, при коэффициенте сигнала пусковой момент в 2 раза меньше, чем при , а скорость холостого хода составляет 0,8 от скорости при . Естественно, что время разгона двигателя с уменьшением коэффициента сигнала растет.

Из выражений для постоянной времени следует, что она зависит от отношения и скорости . Она возрастает с увеличением момента и частоты питающей сети. При увеличении числа полюсов величина уменьшается. Двигатели, рассчитанные на работу при пониженной частоте, несмотря на то, что они обычно выполняются многополюсными, имеют большую постоянную времени, чем машины, рассчитанные на работу при частоте 50 Гц.