МОДУЛЬ № 4

Поверхні ІІ порядку.

Канонічні рівняння поверхонь.

Веремієнко М. О.

Модуль № 4

Поверхні ІІ порядку. Канонічні рівняння поверхонь.

РОЗДІЛ 1. Теоретичні відомості до модуля № 4.

Поверхні ІІ порядку

Означення1. Рівнянням поверхні в деякій афінній системі координат називається рівняння виду F(x,y,z)=0, якому задовольняють координати довільної точки цієї поверхні і не задовольняють координати жодної точки, яка не належить поверхні. Рівняння вищих степенів визначають криволінійну поверхню.

Означення 2. Поверхнею ІІ порядку називається множина всіх точок простору, координати яких задовольняють рівняння:

а₁₁х² + а₂₂у²+ а₃₃z²+ 2a₁₂xy+ 2a₁₃xz+ 2a₂₃yz+ 2a₁₀x+ 2a₂₀y+ 2a₃₀z+ a₀₀ =0

Циліндричні та конічні поверхні.

Означення 3. Циліндричною поверхнею називається поверхня, утворена усіма па­ралельними фіксованому ненульовому вектору ā = {l,m,n} прямими, які перетинають деяку фіксовану криву γ. Ці прямі називаються твір­ними, а крива γ — напрямною циліндричної поверхні.

У найпростіших випадках рівняння циліндричної поверхні можна отримати наступним чином. Нехай у деякій прямокутній декартовій системі координат напрямна циліндричної поверхні задана рівняннями

F(x,y,z) = 0, G(x,y,z) =0,

а твірні паралельні вектору ā = {l,m,n}. Нехай (x',y',z') — довільна точка напрямної. Тоді

F(x',y',z') = 0, G(x',y',z')=0,(1)

а рівняння твірної, яка проходить через точку (х',у',z'), мають вигляд

(2)

Виключаючи x’, у’, z’ з чотирьох рівнянь (1), (2), отримаємо рівня­ння відносно х, у, z, яке і є рівнянням шуканої циліндричної поверхні. Вибравши прямокутну декартову систему координат у просторі так, щоб твірні циліндричної поверхні мали напрям осі аплікат, рівняння цієї циліндричної поверхні можна записати у вигляді

f(x,y) = 0,

де рівняння f(x, у) = 0 визначає на площині Оху криву, отриману в перерізі даної циліндричної поверхні перпендикулярною до осі Оz пло­щиною.

Рівняння, яке розглядається відносно деякої прямокутної декартової системи координат у просторі і зв'язує лише дві координати, є рів­нянням циліндричної поверхні, твірні якої паралельні осі Ох, якщо у рівнянні відсутня координата х, осі Оу, якщо відсутня координата у, і осі Oz, якщо відсутня координата z.

Циліндрична поверхня називається циліндричною поверхнею друго­го порядку, якщо у деякій прямокутній декартовій системі координат вона задається рівнянням f(x,y,z) =0, де f — многочлен другого сте­пеня від змінних x, у та z, розглянутий як функція на R³.

Конічні поверхні.

Означення 4. Конічною поверхнею називається поверхня, утворена усіма прями­ми, які проходять через фіксовану точку S і перетинають деяку фіксо­вану криву γ. Ці прямі називаються твірними, точка S — вершиною, а крива γ — напрямною конічної поверхні.

У найпростіших випадках рівняння конічної поверхні можна отри­мати наступним чином. Нехай у деякій прямокутній декартовій систе­мі координат напрямна конічної поверхні з вершиною S(a, b, с) задана рівняннями

F{x,y,z) = 0, G(x,y,z) =0.

Нехай (x',y',z') — довільна точка напрямної. Тоді

F(x',y',z') = 0, G(x',y',z')=0, (3)

а рівняння твірної, яка проходить через точку (x',y',z'), мають вигляд

(4)

Виключаючи x', y', z' з чотирьох рівнянь (3), (4), отримаємо рівня­ння відносно х, у, z, яке і є рівнянням шуканої конічної поверхні.

Конічна поверхня називається конічною поверхнею другого поряд­ку, якщо у деякій прямокутній декартовій системі координат вона за­дається рівнянням f(x, у, z) = 0, де f — многочлен другого степеня від змінних х, у та z, розглянутий як функція на R³.

Кожне однорідне рівняння другого степеня, яке розглядається від­носно деякої прямокутної декартової системи координат у просторі і пов'язує три координати, визначає початок координат або конічну по­верхню другого порядку з вершиною у початку координат. І навпаки, довільна конічна поверхня другого порядку задається однорідним рів­нянням другого степеня, яке зв'язує три координати, в кожній прямо­кутній декартовій системі координат, початок якої збігається з верши­ною даної конічної поверхні.

Поверхні обертання другого порядку.

Означення 5. Обертанням фігури Ф на кут φ =2π навколо прямої (осі обертання) називається такий рух, при якому кожна точка фігури описує коло з центром на осі обертання, що лежить в площині, яка перпендикулярна до осі обертання.

Означення 6. Поверхня, утворена обертанням кривої навколо прямої (осі), називається поверхнею обертання.

З означень 5 та 6 витікає, що якщо через будь-яку точку поверхні обертання провести площину, перпендикулярну до осі обертання, то вона перетне поверхню по колу з центром на осі обертання.

Розглянемо два способи складання рівняння поверхні обертання.

1 Спосіб.

Будемо будь-яку лінію l розглядати як перетин двох поверхонь, що через неї проходять. Тоді лінія l може бути задана системою двох рівнянь:

(5)

Розв’язавши рівняння (5) відносно x та у, якщо це можливо, отримаємо:

(6)

Очевидно, що рівняння (6) будуть рівняннями тієї ж лінії. Для знаходження рівняння поверхні обертання лінії навколо осі Oz візьмемо довільну точку М (X, Y, Z) на цій поверхні і проведемо через неї площину, перпендикулярну до осі Oz. Ця площина перетне шукану поверхню обертання по колу з центром O' на осі Oz, а лінію l - в точці N (x, у, z),

(О'N)² = x² +y²,

(О'М)² = X² + Y²,

а оскільки точки М і N лежать на одному колі, то О'N = О'М, і тому

X² + Y² = х² +у². (7)

Враховуючи, що точка N лежить на лінії l, маємо:

х = φ (Z), y = ψ (Z).

Підставивши знайдені значення х і у в рівняння (7), одержимо рівняння поверхні обертання лінії l навколо осі Oz:

X² + Y² = φ²(Z) + ψ² (Z). (8)

Навпаки, будь-яке рівняння виду х² +у² = f(z) є рівняння поверхні обертання навколо осі Оz, оскільки при перетині цієї поверхні площинами z = const ми одержимо кола з центром на осі Оz.

З вищесказаного виходить досить простий прийом отримання рівняння поверхні обертання, а саме: для того, щоб одержати рівняння поверхні обертання лінії (5) навколо осі Оz, треба привести ці рівняння до вигляду (6) і скласти квадрати правих і лівих частин рівнянь. Аналогічно можна отримати рівняння поверхонь обертання лінії навколо осей Ох і Оу.

Поверхні обертання другого порядку утворюються обертанням ліній другого порядку навколо їх осей симетрії. Знайдемо рівняння цих поверхонь.

1. Нехай задано рівняння еліпса, розташованого в площині Oxz;

а) Обертаючи еліпс навколо осі Оz, одержимо поверхню, що називається еліпсоїдом обертання. Користуючись правилом, знайдемо її рівняння. З рівняння еліпсу маємо:

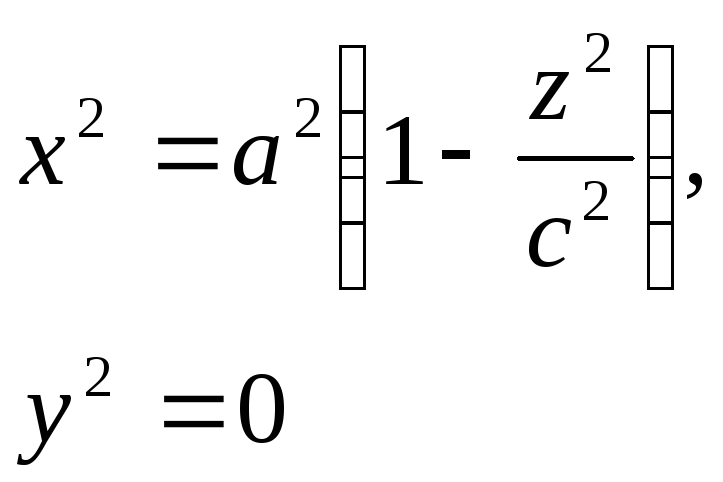
Складаючи ці рівняння отримуємо :

або

б) Обертаючи еліпс навколо осі Ох, одержимо еліпсоїд обертання, рівняння якого має вигляд:

2. Нехай дані рівняння гіперболи, розташованої в площині Охz:

а ) Якщо обертати цю гіперболу навколо дійсної осі Ох, то одержимо поверхню, що називається двопорожнинним гіперболоїдом обертання.

Знайдемо його рівняння. З рівнянь гіперболи маємо:

та у²=0, тоді

б) Обертаючи гіперболу навколо уявної осі Оz, одержимо поверхню, що називається однопорожнинним гіперболоїдом обертання. Рівняння цієї поверхні має вигляд:

2 Спосіб

Н ехай крива F(Y, Z) = 0 (*), що лежить в Oyz обертається навколо Оy. Складемо рівняння поверхні обертання. Нехай М(x,y,z) – будь-яка точка поверхні обертання. Через точку М проведемо площину перпендикулярну до поверхні обертання, що перетинає цю поверхню по колу з центром а точці А. Тоді для точки N маємо:

Y = y (9)

N(0,y,z)

MA=AN

NA=z

(10)

Підставивши (9),(10) в (*) маємо

Правило: щоб одержати рівняння поверхні, утвореної обертанням лінії l, що лежить в Oyz, навколо Оy, треба замінити в рівнянні цієї лінії z на .

Приклад: В площині Oyz задано еліпс. Знайти рівняння поверхні, утвореної обертанням його навколо:

1. осі Оy

2. осі Oz

Канонічні рівняння поверхонь ІІ порядку.

Означення 7. Сферою називається множина точок простору, рівновіддалених від однієї точки, що називається центром сфери, на задану відстань(радіус сфери). Рівняння сфери:

(х-а)²+(у-b)²+(z-c)²=R²,

або

x²+y²+z²-2ax-2by-2cz +a²+b²+c²-R²=0

Рівняння сфери містить чотири незалежні параметри: координати центру і радіус. Рівняння це - другого ступеня, тому сфера - поверхня другого порядку.

Якщо перенести початок координат в центр сфери, то рівняння її прийме простіший вигляд:

х² + у² +z² = R²

З будь-якою прямою лінією сфера має дві спільні точки (дійсні або уявні); якщо обидві точки перетину зливаються, то пряма дотикається до сфери, і тоді відстань її від центру сфери рівна радіусу.

З будь-якою площиною сферична поверхня перетинається по колу (дійсному або уявному). Якщо площина знаходиться від центру на відстані, рівної радіусу, то лінія перетину перетворюється в круг нульового радіусу (одна дійсна точка); площина дотикається сфери, в ній лежать всі прямі, що дотикаються до сфери в даній точці.

Площина, дотична до сфери, в точці (x₁,y₁,z₁) має рівняння_:

(x₁-a)(x₂-a) + (y₁-b)(y₂-b) + (z₁-c)(z₂ -c) = R².

Якщо сфера віднесена до центру, то дотична площина зображається рівнянням:

xx_l + yy₁+ zz₁ = R².

О значення 8. Еліпсоїдом (мал. 1) називається поверхня, яка у деякій прямоку­тній декартовій системі координат, яка називається канонічною систе­мою координат для даного еліпсоїда, визначається рівнянням

мал. 1

Це рівняння називається каноніч­ним рівнянням еліпсоїда, а додатні дійсні числа a, b, c — півосями елі­псоїда. Якщо всі вони різні, то елі­псоїд називається тривісним. Якщо серед цих чисел є принаймні два однакові, то еліпсоїд є поверхнею обертання і називається еліпсоїдом обертання. Якщо ж всі три півосі однакові, то еліпсоїд є сферою. У канонічній системі координат початок координат О є центром симетрії еліпсоїда і називається центром еліпсоїда. Еліпсоїд має три осі симетрії , які збігаються з осями канонічної системи координат і називаються осями еліпсоїда, і три площини симетрії¹, які збігаються з координатними площинами канонічної системи координат. Перерізи еліпсоїда цими площинами називаються головними, а точки перетину еліпсоїда з його осями — вершинами еліпсоїда.

О значення 9. Однопорожнинним гіперболоїдом (мал. 2) називається поверхня, яка у деякій прямокутній декартовій системі координат, яка називає­ться канонічною системою координат для даного однопорожнинного гіперболоїда, визначається рівнянням

Це рівняння називається канонічним рівнянням однопорожнинного гі­перболоїда, а додатні дійсні числа а,b, с — півосями однопорожнинного гіперболоїда. Якщо α = b, то однопорожнинний гіперболоїд є поверхнею обертання і називається однопорожнинним гіперболоїдом обертання.

_{Мал. 2.}

У канонічній системі координат початок координат О є центром симетрії однопорожнинного гіперболоїда і називається центром одно­порожнинного гіперболоїда. Однопорожнинний гіперболоїд має три осі симетрії, які збігаються з осями канонічної системи координат і назива­ються осями однопорожнинного гіперболоїда, і три площини симетрії, які збігаються з координатними площинами канонічної системи координат. Перерізи однопорожнинного гіперболоїда цими площинами на­зиваються головними, причому еліпс, який отримується у перерізі одно­порожнинного гіперболоїда площиною Оху, називається горловим.

Означення 10. Двопорожнинним гіперболоїдом (мал. 3) називається поверхня, яка у деякій прямокутній декартовій системі координат, яка назива­ється канонічною системою координат для даного двопорожнинного гіперболоїда, визначається рівнянням

Мал. 3.

Це рівняння називається канонічним рівнянням двопорожнинного гі­перболоїда, а додатні дійсні числа а, b, с — півосями двопорожнинного гіперболоїда. Якщо а = b, то двопорожнинний гіперболоїд є поверхнею обертання і називається двопорожнинним гіперболоїдом обертання.

У канонічній системі координат поча­ток координат О є центром симетрії дво­порожнинного гіперболоїда і називається центром двопорожнинного гіперболоїда. Двопорожнинний гіперболоїд має три осі симетрії, які збігаються з осями канонічної системи координат і називаються осями двопорожнинного гіперболоїда, і три пло­щини симетрії, які збігаються з координа­тними площинами канонічної системи ко­ординат. Перерізи двопорожнинного гіпер­болоїда площинами Οxz і Oyz називаються головними.

Означення 11. Еліптичним параболоїдом (мал. 4) називається поверхня, яка у деякій прямо­кутній декартовій системі координат, яка називається канонічною системою коорди­нат для даного еліптичного параболоїда, визначається рівнянням

де p i q — деякі додатні дійсні числа, які називаються параметрами елі­птичного параболоїда. Це рівняння називається канонічним рівнянням еліптичного параболоїда. Якщо ρ = q, то еліптичний параболоїд є по­верхнею обертання і називається еліптичним параболоїдом обертання.

Мал. 4.

Еліптичний параболоїд має вісь симетрії, яка збігається з віссю 0z канонічної системи координат і називається віссю еліптичного парабо­лоїда, і дві площини симетрії, які збігаються з площинами Oxz і Оуг канонічної системи координат. Перерізи еліптичного параболоїда цими площинами називаються головними, а точка перетину еліптичного па­раболоїда з його віссю — вершиною еліптичного параболоїда.

Означення 12. Гіперболічним параболоїдом (мал. 5) називається поверхня, яка у деякій прямокутній декартовій системі координат, яка називається ка­нонічною системою координат для даного гіперболічного параболоїда, визначається рівнянням

де ρ і q — деякі додатні дійсні числа, які називаються параметрами гіперболічного параболоїда. Це рівняння називається канонічним рів­нянням гіперболічного параболоїда.

Мал. 5.

Гіперболічний параболоїд має вісь симетрії, яка збігається з віссю Oz канонічної системи координат і називається віссю гіперболічного па­раболоїда, і дві площини симетрії, які збігаються з площинами Oxz і Oyz канонічної системи координат. Перерізи гіперболічного параболої­да цими площинами називаються головними.

Прямолінійні твірні поверхонь другого порядку

Означення 13. Пряма, що лежить на поверхні, називається прямолінійною твірною цієї поверхні. Тобто твірні циліндричних та конічних поверхонь є їх прямолінійними твірними.

Однопорожнинний гіперболоїд

має дві серії прямолінійних твірних, які визначаються рівняннями

де α, β — дійсні числа, принаймні одне з яких відмінне від нуля. Будь-які дві прямолінійні твірні однієї серії мимобіжні. Будь-які дві прямо­лінійні твірні різних серій або перетинаються, або паралельні. Через кожну точку даної поверхні проходить по одній твірній з кожної серії.

Гіперболічний параболоїд

має дві серії прямолінійних твірних, які визначаються рівняннями

де λ – дійсне число. Будь-які дві прямо­лінійні твірні однієї серії мимобіжні. Будь-які дві прямо­лінійні твірні різних серій перетинаються. Через кожну точку даної поверхні проходить по одній твірній з кожної серії.

Перетин поверхні другого порядку з прямою

Нехай поверхня другого порядку Φ задана своїм канонічним рівня­нням. Дослідимо, як розташована відносно даної поверхні пряма

x=x₀+lt,

y=y₀+mt, (11)

z=z₀+nt.

Підставляючи вирази для x,y i z з параметричних рівнянь пря­мої (11) у рівняння поверхні Ф, отримуємо відносно t рівняння

At² + 2Bt + C = 0 (12)

не вище другого порядку, де А, В, С — деякі дійсні числа. Розглянемо випадки.

1. А≠0, рівняння (12) є квадратним. В цьому випадку кажуть, що пряма (11) має неасимптотичний напрям відносно поверх­ні Ф. Нехай D — дискримінант рівняння (12). Тоді, якщо:

• D > 0, то рівняння (12) має два різних дійсних кореня, і кажуть, що пряма (11) перетинає поверхню Φ у двох точках;

• D = 0, то рівняння (12) має два рівних дійсних кореня, і кажуть, що пряма (11) дотикається до поверхні Ф;

• D < 0, то рівняння (12) не має дійсних коренів, і ка­жуть, що пряма (11) не перетинає поверхню Ф.

2. А = 0, рівняння (12) не є квадратним. В цьому випадку ка­жуть, що пряма (11) має асимптотичний напрям відносно по­верхні Ф. При цьому, якщо:

• В ≠ 0, то рівняння (12) має один дійсний корінь, і кажуть, що пряма (11) перетинає поверхню Φ в одній точці;

• В = 0, С ≠ 0, то рівняння (12) не має розв'язків, і кажуть, що пряма (11) є асимптотою поверхні Ф;

• В = С = 0, то рівняння (12) перетворюється на тото­жність, і кажуть, що пряма (11) належить поверхні Φ (тобто є прямолінійною твірною поверхні Ф).

Дотична площина і нормаль

Означення 14. Геометричне місце прямих, які проходять через точку Μ поверхні другого порядку (яка у випадку конічної поверхні не є її вершиною) і дотикаються до даної поверхні або належать їй, є площина. Ця площина називається дотичною площиною до даної поверхні в точці М.

Означення 15. Нормаллю до поверхні другого порядку в точці Μ цієї поверхні на­зивається пряма, яка проходить через дану точку перпендикулярно до дотичної площини до цієї поверхні в точці Μ.

Рівняння дотичної площини до поверхні другого порядку в її точці М_о(х_о,y_о, z_о) для різних поверхонь має вигляд:

Рівняння поверхні	Рівняння дотичної площини