§ 5. Конічні поверхні

Означення 5.1. Поверхня, утворена внаслідок руху прямої, яка проходить через дану точку M₀ і перетинає дану криву L, називається конічною поверхнею або конусом. При цьому задана точка називається вершиною конічної поверхні, крива L - напрямною кривою. Прямі, які повністю лежать на поверхні конуса, проходять через його вершину і перетинають напрямну криву, називаються твірними конуса (рис. 13).

З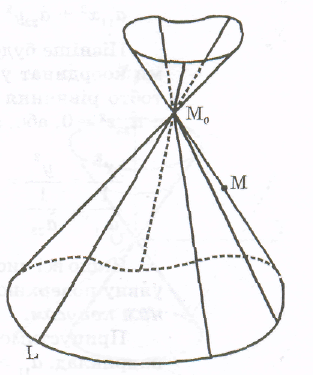 цього означення випливає, що поверхня буде конусом з вершиною в точці М₀ тоді і тільки тоді, коли разом з деякою точкою М цій поверхні належать усі точки прямої М₀М.

Означення 5.2. Функція F(x; y; z) називається однорідною, якщо для довільного t ≠ 0 виконується умова F(tx; ty; tz) = φ(t)F(x; y; z).

Наприклад, F(x; у; z) = xy³ + x⁴ – x² z² - однорідна функція, бо

F(tx; ty; tz) = tx • t³ y³ + t⁴ x⁴ – t² x² • t² z² = = t⁴ (xy³ + x4 – x² z²) = t⁴ F(x; y; z).

Припустимо тепер, що прямокутна система координат вибрана так, що її початок збігається з вершиною конічної Рис.13 поверхні.

Теорема 3. Якщо F(x; у; z) - однорідна функція, а рівняння

F(x;y;z) = 0 (13)

задає деяку поверхню σ в просторі, то це буде конічна поверхня з вершиною в початку координат.

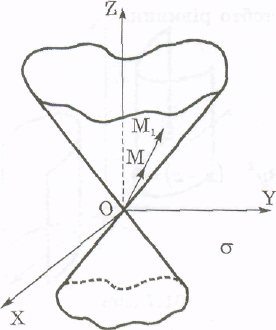
Доведення. Нехай М(х; у; z) - довільна точка цієї поверхні, а М₁ (x₁ ;y₁ ; z₁ ) - довільна точка, яка лежить на прямій ОМ (рис. 14). Покажемо, що точка M₁ також належить даній поверхні. М є σ, тому F(x; у; z) = 0.

Рис.14

Розглянемо вектори

ОМ (х; у; z) і ОМ₁ (х₁; y₁; z₁). Оскільки ОМ || ОМ₁ ,

то звідки x₁=tx, y₁=ty, z₁=tz.

Тоді F(x_1; y₁; z₁ ) = F(tx; ty; tz) = φ(t)F(x; y; z) = 0, оскільки F(x; y; z) = 0.

Таким чином, разом з точкою М даній поверхні належить і точка M₁ , що лежить на прямій ОМ. Звідси випливає, що рівняння (13) є рівнянням конічної поверхні з вершиною в початку координат. Теорему доведено. ■

Будемо розглядати тепер конічні поверхні другого порядку. З доведеної теореми випливає, що загальне рівняння конічної поверхні другого порядку має вигляд:

a₁₁x² + a₂₂y² +a₃₃z² + 2a₁₂xy +2a₁₃xz + 2a₂₃yz = 0. (14)

Пізніше буде встановлено, що за допомогою перетворення системи координат у рівнянні (14) можна позбутися добутків змінних, тобто рівняння (14) може бути зведене до вигляду

a₁₁x² + a₂₂y² + a₃₃z² = 0, або, якщо a₁₁ a₂₂ a₃₃ ≠ 0, до вигляду

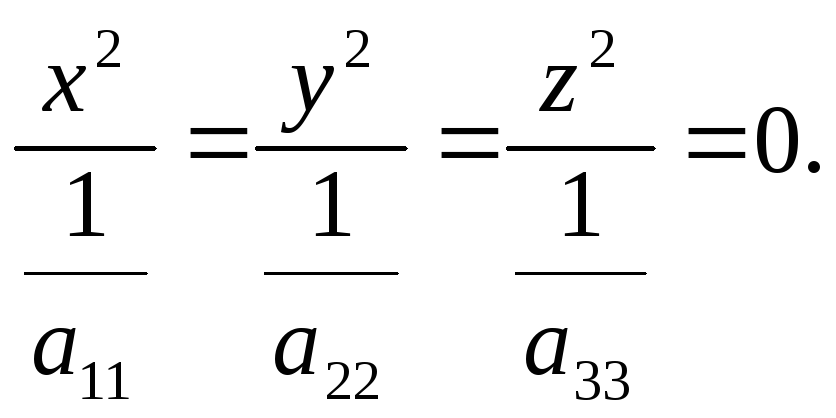(15)

Якщо всі числа а₁₁, а₂₂, а₃₃ одного знаку, то це рівняння задає деяку уявну поверхню з однією дійсною точкою (0; 0; 0). її називають уявним конусом.

Припустимо, що серед цих чисел є числа різного знаку. Нехай, наприклад, а₁₁ > 0, a₂₂> 0, а₃₃ < 0. Тоді, ввівши відповідні позначення, рівняння (15) можна записати у вигляді

(16)

Це рівняння називається канонічним рівнянням конуса. З нього випливають такі його властивості:

1. Конус симетричний відносно координатних площин, координатних осей і початку координат, бо всі змінні входять у його рівняння в парних степенях.

2. Якщо цей конус перетнути площиною z =h, паралельною до площини OXY, то в перерізі утвориться крива, проекція якої на площину OXY має рівняння

Або

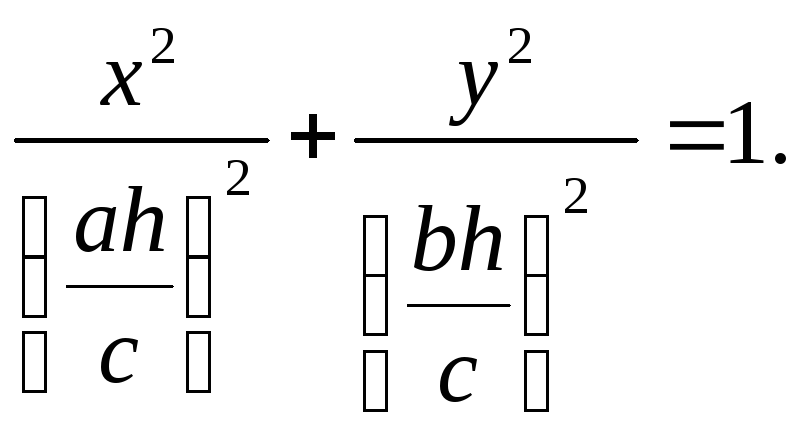
Це є рівняння еліпса.

Отже, напрямною кривою даного конуса є еліпс. При зростанні абсолютної величини h розміри еліпса збільшуються. Вісь OZ у цьому випадку називається віссю конуса (рис. 15).

Якщо віссю конуса є вісь OY, то рівняння конічної поверхні другого порядку таке:

Якщо ж віссю конуса є вісь ОХ, то його рівняння буде

На прикладі покажемо, як знаходити рівняння довільної конічної поверхні, якщо відомі її вершина і напрямна крива.

Приклад. Скласти рівняння конічної поверхні з вершиною у точці М₀ (l; 0; 1) і напрямною L, що лежить у площині OXY і задається рівнянням

x² + y² – y = 0.

Розв'язання. Через довільну точку М(х; у; z) конічної поверхні проведемо твірну М₀М (рис. 16). Вона перетне напрямну в деякій точці М'(х'; у'; z'). М' є L, тому

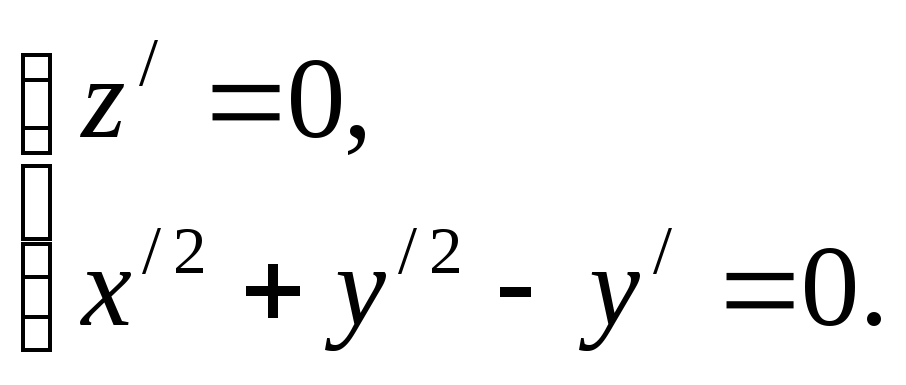
Рис. 15

Запишемо рівняння твірної конуса за двома точками М₀ (1; 0; 1) і М'(x'; у'; 0):

Змінні х, у, z у цьому рівнянні є координатами точок твірної, а отже, і точок конічної поверхні. Складемо систему рівнянь і вилучимо з неї x', у', z':

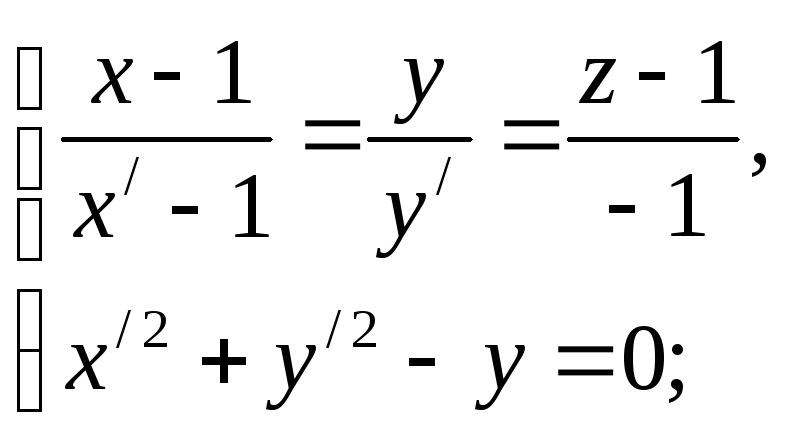
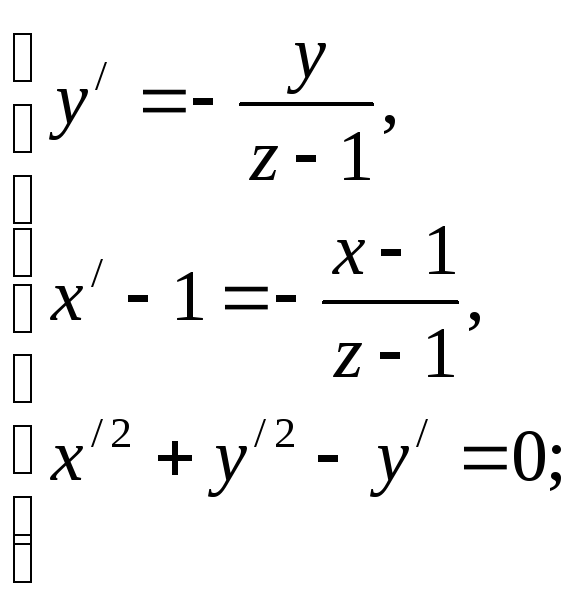
Рис.16

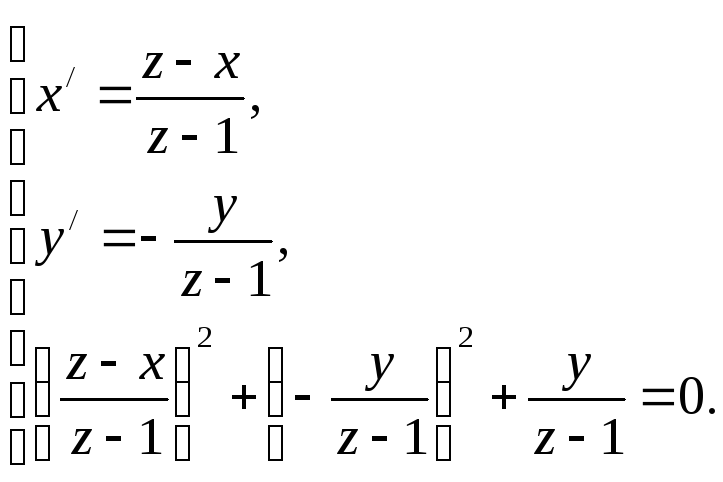
Із останнього рівняння маємо:

(z-x)² + y² + y(z-1) = 0

Це і є рівняння шуканої конічної поверхні.

§ 6. Еліпсоїд

Означення 6.1. Еліпсоїдом називається поверхня, яка в деякій прямокутній системі координат задається рівнянням

(17)

Це рівняння називається канонічним рівнянням еліпсоїда, а система координат, відносно якої задано цей еліпсоїд, називається канонічною системою координат.

Аналізуючи рівняння (17), дослідимо основні властивості еліпсоїда, визначимо його форму і побудуємо зображення.

Не втрачаючи загальності, можна вважати, що а > 0, b > 0, с > 0.

Властивості еліпсоїда.

1. Еліпсоїд не проходить через початок координат, бо координати точки О(0; 0; 0) не задовольняють рівняння (17).

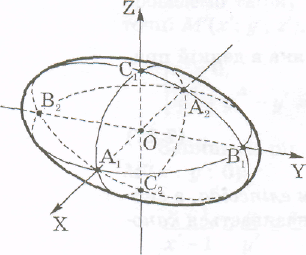
2. Еліпсоїд перетинає кожну із координатних осей у двох точках, симетричних відносно початку координат, а саме:

вісь ОХ у точках А₁(а; 0; 0) і А₂(-а; 0; 0),

вісь OY у точках В₁(0; b; 0) і В₂(0; -b; 0),

вісь OZ у точках С₁(0; 0; с) і С₂(0; 0; -с).

Ці точки називаються вершинами еліпсоїда, відрізки AА₂ = 2а, ВВ₂ = 2b, CC₂ = 2с- осями еліпсоїда, числа а, b, с - півосями еліпсоїда.

3.Еліпсоїд симетричний відносно всіх координатних площин, координатних осей і початку координат, бо всі змінні входять у його рівняння в парних степенях.

4. Із рівняння (17) випливає, що 1, тобто а,

с.

Це означає, що еліпсоїд є обмеженою поверхнею, яка міститься всередині прямокутного паралелепіпеда, обмеженого площинами х = ±а, у = ±b, z = ±с.

5.Якщо еліпсоїд перетнути площиною 2 = h (h\ < с), паралельною площині OXY, то в перетині утвориться еліпс, рівняння проекції якого на площину OXY у системі координат цієї площини має вигляд:

.

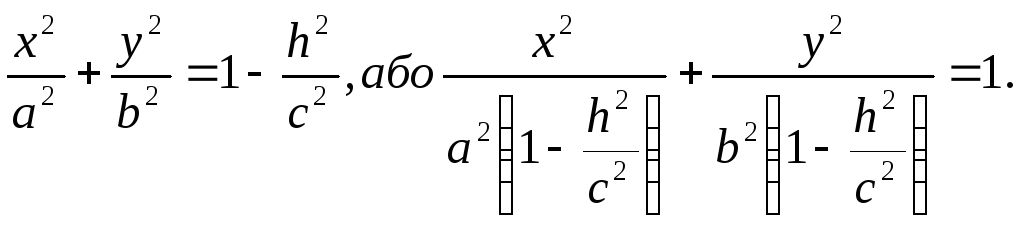Розміри цього еліпса збільшуються зі зменшенням і зменшуються зі збільшенням |h|.

Аналогічне спостерігається і при перетині еліпсоїда площинами, паралельними до інших координатних площин.

Виходячи із цих властивостей можна побудувати зображення еліпсоїда (рис. 17).

Рис.17

Якщо в рівнянні (17) два параметри рівні між собою, наприклад, а = b, то дістанемо поверхню обертання - еліпсоїд обертання:

Рис. 18

Ця поверхня утворена внаслідок обертання еліпса з півосями а, с навколо осі OZ.

Якщо ж а = b = с, то із (17) матимемо:

x²+y²+z²=a².

Це рівняння сфери з центром у початку координат. Отже, сфера є частковим випадком еліпсоїда. Справедлива й така теорема.

Теорема 3. При перетині еліпсоїда довільною площиною в перерізі утворюється еліпс.

Доведення. Оскільки еліпсоїд є обмеженою поверхнею, то при перетині його з будь-якою площиною утвориться обмежена крива другого порядку (див. теорему 1). Тому ця крива не може бути ні параболою, ні гіперболою, ні парою прямих. Отже, вона є еліпсом, що й треба було довести (рис. 18).■

Приклад. Записати рівняння еліпсоїда, осі якого збігаються з осями координат, і який проходить через точку М(2; 0: 1) та перетинає площину OXY по еліпсу

(18)

Розв'язання. Якщо осі координат збігаються з осями еліпсоїда, то ця система координат є канонічною, тому рівняння еліпсоїда матиме вигляд:

(17)

Площина ОХУ перетинає цей еліпсоїд по еліпсу = 1 . Зіставляючи останнє рівняння із (18), матимемо: а² = 8, b²= 1. Тоді рівняння (17) набуде вигляду: = 1.

За умовою точка М(2; 0; 1) лежить на цій поверхні, тому

звідки с² = 2.

Отже, рівняння даного еліпсоїда = 1.

Відповідь. = 1.