§ 2. Метод перерізів вивчення форми поверхні

Цей метод ґрунтується на такій теоремі.

Теорема 2. Якщо поверхню, задану рівнянням

F(х; у; z) = 0, (1)

перетнути площиною z = h, паралельною до площини ОХY, то в перерізі утвориться лінія, проекція якої на площину ОХY у напрямку осі ОZ в системі координат ОХY задається рівнянням

F(х; у; h) = 0. (4)

Доведення. Нехай деяку поверхню σ перетнули площиною z = h і в перерізі отримали лінію γ (рис. 2). γ^,- проекція лінії γ на площину ОХY у напрямку осі ОZ. Покажемо, що рівняння (4) є рівнянням лінії γ^, у площині ОХY.

Нехай М'(х; у) належить лінії γ^,. Точка М' є проекцією деякої точки М(х; у; h), що належить лінії γ. Оскільки ця точка М належить даній поверхні, то її координати задовольняють рівняння поверхні (1), тобто F(х; у, h) = 0. Таким чином, координати довільної точки М(х; у) кривої γ^, задовольняють рівняння (4).

Нехай тепер точка N´(x₁; y₁) площини ОХY не належить лінії γ'. Ця точка є проекцією деякої точки N(x₁ ,y₁ ,h), яка лежить у площині z =h, але не належить лінії γ. Отже, ця точка не лежить і на поверхні σ . Тому F(х₁; у₁, h) ≠ 0.

Таким чином, рівняння (4) задовольняють координати точок кривої γ^, і тільки вони. Тому рівняння (4) є рівнянням кривої γ^,, що й треба було довести.

Аналогічно, якщо поверхню (1) перетнути площиною у = h, паралельною до площини ОХZ, то рівняння проекції лінії перетину у напрямку ОY на площину ОХZ у цій площині матиме рівняння F(х; h; z) = 0.

Я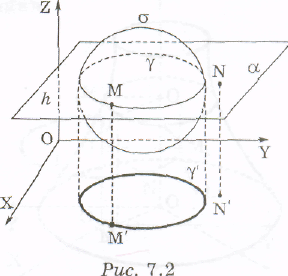кщо ж поверхню (1) перетнути площиною x=h, паралельною до ОУZ, то рівняння проекції лінії перетину в напрямку осі ОХ на площину ОYZ матиме вигляд F(h у; z) = 0.

Ця теорема дозволяє будувати карту перерізів поверхні на ту чи іншу координатну площину. Якщо, наприклад, поверхню перетнути площинами z = h₁ ,z = h₂, .., z = h_n, паралельними до площини ОХY, і відповідні лінії перерізів спроектувати на площину ОХY, то на цій площині дістанемо карту відповідних перерізів, рівняння яких будуть F(x;у; h₁) = 0, F(х; у; h₂) = 0, .., F(х; у; h_n) = 0 (рис. 3).

Ця карта перерізів є сукупністю кривих, за формою і розміщенням яких можна судити про форму поверхні.

§ 3. Поверхні обертання

Означення 3.1. Нехай у деякій площині лежить пряма І і крива L. Поверхня, яка утворюється внаслідок обертання кривої L навколо прямої l, називається поверхнею обертання (рис. 4).

П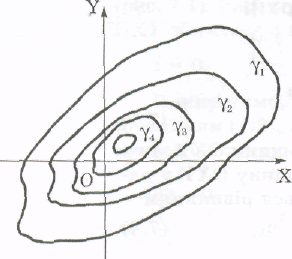ри цьому пряма І називається віссю обертання, а крива L - твірною або меридіаном поверхні обертання. Кожна точка М кривої L при цьому обертається по колу, площина якого перпендикулярна до осі l, а центр знаходиться на осі І. Це коло називається паралеллю поверхні обертання.

Складемо рівняння поверхні обертання.

Рис.3

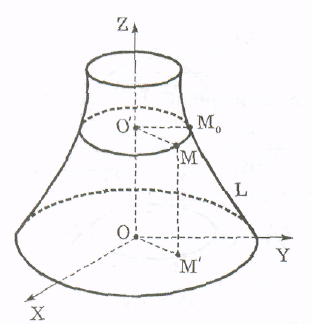
Виберемо прямокутну систему координат так, щоб вісь ОZ збігалася з віссю обертання І, а лінія L, яка обертається, була розміщена в площині ОYZ (рис.5). Нехай крива L у системі координат ОYZ задається рівнянням

F(у; z) = 0, (5)

а точка М(х; у; z) - довільна точка поверхні обертання. Через цю точку проведемо площину, перпендикулярну до осі ОZ. Вона перетне поверхню по колу, яке є паралеллю даної поверхні обертання. Припустимо, що це коло перетинається з лінією L у точці М₀(у₀; z₀). Оскільки точка М₀ є L, то її координати задовольняють рівняння (5):

F(y₀ ;z₀ )=0 (6)

Рис.4

Центр цього кола позначимо О'. О'М — радіус паралелі, тому О'М = О'М0. Але якщо точку М спроектувати на площину ОХY, то її

проекцією буде точка М'(х; у) і О'М = ОМ' = √х² + у² , а О'М₀ = ׀y₀׀

Звідси випливає, що |y₀| =

або y₀=

Підставивши одержані формули в (6),отримаємо

F( (7)

Рис.5

Отже, координати довільної точки М поверхні обертання задовольняють рівняння (7).

Припустимо тепер, що координати деякої точки N(x₁;y₁;z₁) задовольняють рівняння (7), тобто

F( (8)

Покажемо, що ця точка належить даній поверхні обертання. Проведемо через точку N площину, перпендикулярну до осі ОZ (рис. 6).

Припустимо, що ця площина перетинає вісь ОZ у точці О'. Побудуємо в цій площині коло з центром О' радіусом О'N. Нехай це коло перетинає площину ОYZ в точці М(₀(у₀; z₀). Тоді O^, N=

Звідси випливає, що y₀₌якщо y_0, і y₀=-якщо y₀> 0.

Крім того, оскільки точки N і М₀ лежать у площині, паралельній до площини ОХY, то z₁ = z₀. Тоді рівність (8) запишеться так: F(y₀; z₀) = 0, звідки випливає, що точка М₀ належить меридіану, а це означає, що точка N лежить на даній поверхні обертання.

Отже, рівняння (7) - рівняння поверхні обертання.

Аналогічно можна встановити, що коли крива задана рівнянням F(у; z) = 0 у площині ОYZ і обертається навколо осі ОY, то рівняння поверхні обертання матиме вигляд F(y;

Якщо крива знаходиться у площині ОХZ, задана рівнянням F(х; z) = 0 і обертається навколо осі ОХ, то рівняння поверхні обертання

F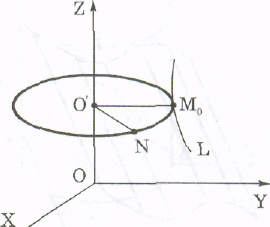(x;.

В результаті приходимо до такого правила складання рівняння поверхні обертання: щоб скласти рівняння поверхні обертання, необхідно в рівнянні лінії, яка обертається, залишити без змін ту змінну, яка відповідає осі обертання, а другу змінну замінити на корінь квадратний, взятий зі знаками «+» та «-», з суми квадратів цієї ж змінної і тієї змінної, яка відсутня в рівнянні кривої.

Рис. 6

Приклад. Дано еліпс, розміщений у площині ОYZ:

Записати рівняння поверхні обертання, утвореної при обертанні цього еліпса навколо осі ОZ.

Розв'язання. За формулою (7) рівняння цієї поверхні обертання має вигляд:

Ця поверхня називається еліпсоїдом обертання.