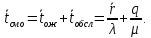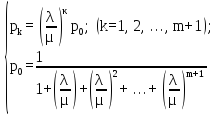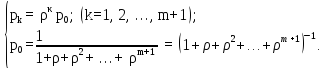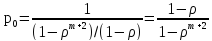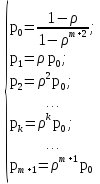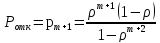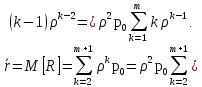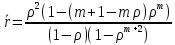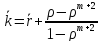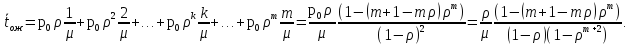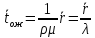- •Оглавление
- •Понятие системы интегрального обслуживания
- •Математическая модель одноканальной смо с отказами
- •Системы связи
- •Технология atm
- •Концептуальные основы атм
- •Atm как технология лвс
- •Atm как современная инфраструктура
- •Концептуальные основы технологии atm
- •Принципы синхронизации в атм
- •Структура стека протоколов атм
- •Физический уровень
- •Уровень атм
- •Уровень адаптации атм
- •Форматы атм
- •Номера виртуальных каналов и виртуальных путей
- •Типы передаваемых данных
- •Приоритеты селлов в системе
- •Технология gsm tdma Частотный структура стандарта gsm
- •1.2. Структурная схема и состав оборудования сетей связи
- •1.4. Структура служб и передача данных в стандарте gsm
- •1.6. Структура тdма кадров и формирование сигналов в стандарте gsm
- •Технология gprs
- •Технология cdma
- •1. Основные принципы cdma
- •2. Отличия cdma от других стандартов
- •3. Услуги в сетях cdma
- •4. Общая характеристика и принципы функционирования
- •5. Технология мультидоступа
- •6. Развитие и перспективы стандарта cdma
- •Сравнительный анализ технологий сотовой связи
- •4. Пути развития сетей 3-го поколения.
- •6. Сравнение технологий 2-го поколения (2g)
- •7. Эволюционные пути развития.
- •Технология WiMax
- •Принцип работы WiMax
- •История развития проекта WiMax
- •Перспективы WiMax в России
- •Заключение
- •Системы определения местоположения Технологии определения местоположения
- •Методы определения местоположения
- •Спутниковые системы навигации
- •Принцип работы спутниковых систем навигации
- •Технические параметры систем gps и глонасс
- •Основные различия спутниковых систем навигации
- •Наземный сегмент системы gps
Министерство образования и науки Российской Федерации
Санкт-Петербургский государственный политехнический университет
Факультет технической кибернетики
кафедра “Системный анализ и управление”
Цифровые сети интегрального обслуживания
к.т.н. доцент Хлопин Сергей Владимирович
Санкт-Петербург
2011
Оглавление
Понятие системы интегрального обслуживания 3
Математическая модель одноканальной СМО с отказами 3
Системы связи 10
Технология ATM 14
Концептуальные основы технологии ATM 31
Структура стека протоколов АТМ 47
Форматы АТМ 51
Технология GSM TDMA 61
Частотный структура стандарта GSM 61
Технология GPRS 91
Технология CDMA 98
1. Основные принципы CDMA 98
2. Отличия CDMA от других стандартов 100
3. Услуги в сетях CDMA 102
4. Общая характеристика и принципы функционирования 105
5. Технология мультидоступа 113
6. Развитие и перспективы стандарта CDMA 115
Сравнительный анализ технологий сотовой связи 120
Технология WiMAX 140
Системы определения местоположения 159
Технологии определения местоположения 159
Методы определения местоположения 160
Спутниковые системы навигации 169
Принцип работы спутниковых систем навигации 170
Технические параметры систем GPS и ГЛОНАСС 171
Основные различия спутниковых систем навигации 173
Наземный сегмент системы GPS 176
Понятие системы интегрального обслуживания
Система массового обслуживания (СМО) - система, которая производит обслуживание поступающих в неё требований. Обслуживание требований в СМО производится обслуживающими приборами. Классическая СМО содержит от одного до бесконечного числа приборов. В зависимости от наличия возможности ожидания поступающими требованиями начала обслуживания СМО подразделяются на
-
системы с потерями, в которых требования, не нашедшие в момент поступления ни одного свободного прибора, теряются;
-
системы с ожиданием, в которых имеется накопитель бесконечной ёмкости для буферизации поступивших требований, при этом ожидающие требования образуют очередь;
-
системы с накопителем конечной ёмкости (ожиданием и ограничениями), в которых длина очереди не может превышать ёмкости накопителя; при этом требование, поступающее в переполненную СМО (отсутствуют свободные места для ожидания), теряется.
Выбор требования из очереди на обслуживание производится с помощью так называемой дисциплины обслуживания. Их примерами являются FCFS/FIFO (пришедший первым обслуживается первым), LCFS/LIFO (пришедший последним обслуживается первым), RANDOM (случайный выбор). В системах с ожиданием накопитель в общем случае может иметь сложную структуру.
Математическая модель одноканальной смо с отказами
Рассмотрим
одноканальную систему массового
обслуживания с ожиданием, в которую
поступает поток пакетов с интенсивностью
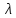 ;
интенсивность обработки
;
интенсивность обработки
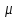 ,
т. е. в среднем непрерывно занятый канал
будет выдавать
,
т. е. в среднем непрерывно занятый канал
будет выдавать
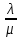 обработанных пакетов в единицу (времени).
Пакет, поступивший в момент, когда канал
занят, становится в очередь и ожидает
обработки.
обработанных пакетов в единицу (времени).
Пакет, поступивший в момент, когда канал
занят, становится в очередь и ожидает
обработки.
Предположим сначала, что количество мест в очереди ограничено числом m, т. е. если пакет пришел в момент, когда в очереди уже стоит m пакетов, он покидает систему не обработанным. В дальнейшем, устремив m к бесконечности, мы получим характеристики одноканальной СМО без ограничений длины очереди.
Будем нумеровать состояния СМО по числу пакетов, находящихся в системе (как обрабатываемых, так и ожидающих обработки):
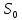 — канал
свободен;
— канал
свободен;
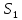 — канал
занят, очереди нет;
— канал
занят, очереди нет;
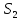 — канал
занят, один пакет стоит в очереди;
— канал
занят, один пакет стоит в очереди;
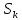 — канал
занят, k - 1 пакетов стоит в очереди;
— канал
занят, k - 1 пакетов стоит в очереди;
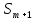 — канал
занят, t пакетов стоит в очереди.
— канал
занят, t пакетов стоит в очереди.
Схема
одноканальной СМО с ожиданием показана
на рис. 1. Все интенсивности потоков
событий, переводящих в систему по
стрелкам слева направо, равны
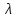 ,
а справа налево —
,
а справа налево —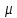 .
Действительно, по стрелкам слева направо
систему переводит поток пакетов (как
только придет пакет, система переходит
в следующее состояние), справа же налево
— поток «освобождений» занятого канала,
имеющий интенсивность
.
Действительно, по стрелкам слева направо
систему переводит поток пакетов (как
только придет пакет, система переходит
в следующее состояние), справа же налево
— поток «освобождений» занятого канала,
имеющий интенсивность
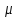 (как только будет обработан очередной
пакет, канал либо освободится, либо
уменьшится число пакетов в очереди).
(как только будет обработан очередной
пакет, канал либо освободится, либо
уменьшится число пакетов в очереди).
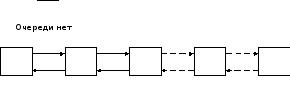
Рисунок. 1 Одноканальная СМО с ожиданием.
Изображенная на рис. 1 схема, представляет собой схему размножения и гибели. Напишем выражения для предельных вероятностей состояний:
|
|
(1) |
или
с использованием
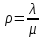 :
:
|
|
(2) |
Последняя
строка в (2) содержит геометрическую
прогрессию с первым членом 1 и знаменателем
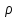 ;
откуда получаем:
;
откуда получаем:
|
|
(3) |
в связи с чем, предельные вероятности принимают вид:
|
|
(4) |
Выражение
(3) справедливо только при
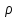 < 1 (при
< 1 (при
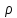 = 1 она дает неопределенность вида 0/0).
Сумма геометрической прогрессии со
знаменателем
= 1 она дает неопределенность вида 0/0).
Сумма геометрической прогрессии со
знаменателем
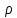 = 1 равна m + 2, и в этом случае
= 1 равна m + 2, и в этом случае
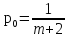
Определим
характеристики СМО: вероятность отказа
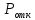 ,
относительную пропускную способность
q, абсолютную пропускную способность
А, среднюю длину очереди
,
относительную пропускную способность
q, абсолютную пропускную способность
А, среднюю длину очереди
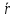 ,
среднее число заявок, связанных с
системой
,
среднее число заявок, связанных с
системой
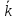 ,
среднее время ожидания в очереди
,
среднее время ожидания в очереди
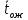 ,
среднее время пребывания заявки в СМО
,
среднее время пребывания заявки в СМО
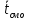 .
.
Вероятность отказа. Очевидно, пакет получает отказ только в случае, когда канал занят и все т мест в очереди тоже:
|
|
(5) |
Относительная пропускная способность:
|
|
(6) |
Абсолютная пропускная способность:
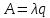
Средняя
длина очереди. Найдем среднее число
 пакетов, находящихся в очереди, как
математическое ожидание дискретной
случайной величины R — числа пакетов,
находящихся в очереди:
пакетов, находящихся в очереди, как
математическое ожидание дискретной
случайной величины R — числа пакетов,
находящихся в очереди:
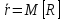
С
вероятностью
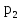 в очереди стоит один пакет, с вероятностью
в очереди стоит один пакет, с вероятностью
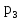 — два пакета, с вероятностью
— два пакета, с вероятностью
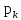 в очереди стоит k - 1 пакетов, и т. д.,
откуда:
в очереди стоит k - 1 пакетов, и т. д.,
откуда:
|
|
(7) |
Поскольку
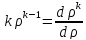 ,
сумму в (7) можно трактовать как производную
по
,
сумму в (7) можно трактовать как производную
по
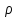 от суммы геометрической прогрессии:
от суммы геометрической прогрессии:
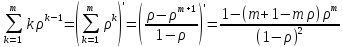 Подставляя
данное выражение в (7) и используя
Подставляя
данное выражение в (7) и используя
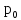 из (4), окончательно получаем:
из (4), окончательно получаем:
|
|
(8) |
Среднее
число пакетов, находящихся в системе.
Получим далее формулу для среднего
числа
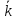 пакетов, связанных с системой (как
стоящих в очереди, так и находящихся на
обработке). Поскольку
пакетов, связанных с системой (как
стоящих в очереди, так и находящихся на
обработке). Поскольку
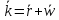 ,
где
,
где
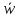 — среднее число пакетов, находящихся
под обслуживанием, а k известно, то
остается определить
— среднее число пакетов, находящихся
под обслуживанием, а k известно, то
остается определить
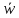 .
Поскольку канал один, число обслуживаемых
пакетов может равняться 0 (с вероятностью
.
Поскольку канал один, число обслуживаемых
пакетов может равняться 0 (с вероятностью
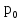 )
или 1 (с вероятностью 1 -
)
или 1 (с вероятностью 1 -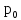 ),
откуда:
),
откуда:
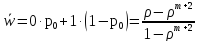
и среднее число пакетов, связанных с СМО, равно
|
|
(9) |
Среднее
время ожидания пакета в очереди. Обозначим
его
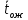 ;
если пакет приходит в систему в какой-то
момент времени, то с вероятностью
;
если пакет приходит в систему в какой-то
момент времени, то с вероятностью
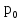 канал не будет занят, и ему не придется
стоять в очереди (время ожидания равно
нулю). С вероятностью
канал не будет занят, и ему не придется
стоять в очереди (время ожидания равно
нулю). С вероятностью
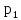 он придет в систему во время обслуживания
какого-то пакета, но перед ним не будет
очереди, и пакет будет ждать начала
своей обработки в течение времени
он придет в систему во время обслуживания
какого-то пакета, но перед ним не будет
очереди, и пакет будет ждать начала
своей обработки в течение времени
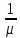 (среднее время обработки одного пакета).
С вероятностью
(среднее время обработки одного пакета).
С вероятностью
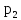 в очереди перед обрабатываемым пакетом
будет стоять еще один, и время ожидания
в среднем будет равно
в очереди перед обрабатываемым пакетом
будет стоять еще один, и время ожидания
в среднем будет равно
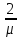 ,
и т. д.
,
и т. д.
Если
же k = m + 1, т. е. когда вновь приходящий
пакет застает канал обслуживания занятым
и m пакетов в очереди (вероятность этого
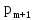 ),
то в этом случае пакет не становится в
очередь (и не обрабатывается), поэтому
время ожидания равно нулю. Среднее время
ожидания будет равно:
),
то в этом случае пакет не становится в
очередь (и не обрабатывается), поэтому
время ожидания равно нулю. Среднее время
ожидания будет равно:
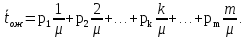
Если подставить сюда выражения для вероятностей (4.4), получим:
|
|
(10) |
Здесь
использованы соотношения (7), (8) (производная
геометрической прогрессии), а также
 из (4). Сравнивая это выражение с (8),
замечаем, что иначе говоря, среднее
время ожидания равно среднему числу
пакетов в очереди, деленному на
интенсивность потока поступления
пакетов.
из (4). Сравнивая это выражение с (8),
замечаем, что иначе говоря, среднее
время ожидания равно среднему числу
пакетов в очереди, деленному на
интенсивность потока поступления
пакетов.
|
|
(11) |
Среднее
время пребывания пакета в системе.
Обозначим
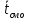 математическое ожидание случайной
величины — время пребывания пакета в
СМО, которое складывается из среднего
времени ожидания в очереди
математическое ожидание случайной
величины — время пребывания пакета в
СМО, которое складывается из среднего
времени ожидания в очереди
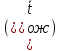 и среднего времени обслуживания
и среднего времени обслуживания
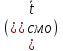 .
Если загрузка системы составляет 100 %,
очевидно,
.
Если загрузка системы составляет 100 %,
очевидно,
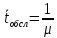 ,
в противном же случае
,
в противном же случае
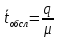 .
Отсюда:
.
Отсюда: